求最长回文子串——Manacher算法详解

回文子串问题

回文子串问题通常会给出一个字符串，然后找出这个字符串中最长的回文子串。
回文串即为正读和反读一致的字符串，比如”aa"，“abba”，"abcba"等。判别一个字符串是否为回文串很容易想到的方法是：

设立两个游标，分别在串的最左和最右，让这两个游标向对方逼近的同时比较这两个游标的值

但是这里我们要讨论的是回文子串，所以上述方法暴露出一个严重的缺陷：难以确定右游标（因为左游标右边的所有字符都可以是右游标）。所以这里我们需要转换思维，不从两边逼近，而是从中间向两边扩散，这时候就要区分串的个数是奇数还是偶数了。

规律1：
奇数串，如aabaa，中间的字符可以是任意的，以这个字符为轴，轴两边的字符是一一对应相等的。
偶数串，如baab，可以假设中间有一条轴，两边的字符必须一一对应。

准备过程

令n为字符串的长度，最容易想到的方法就是枚举每一个可能的字符串，一共有n^2 数量级的子串，判别每一个子串是否是回文串需要n数量级的时间，所以时间复杂度为O(n^3)
我们当然不推荐这样的方法，但是可以作为引导，来弥补这种算法的缺陷。为了便于理解，我们引入“对称轴”的概念，如下图：

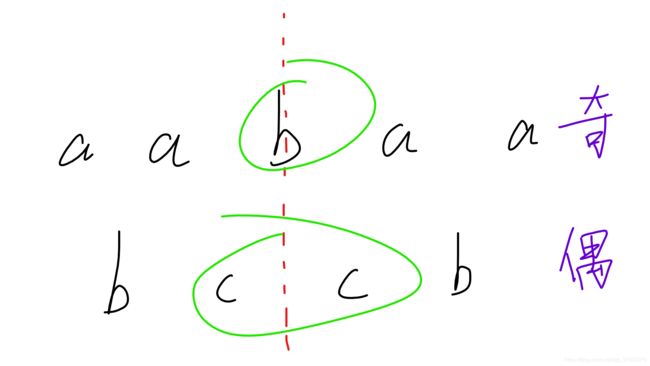
以轴为界，轴两边的字符是关于轴镜像对称的，奇数串（字符个数为奇数）的轴为中间的字符，偶数串的轴为中间的两个字符。

规律2：
字符串的每一个字符（偶数串为两个连续字符）都可能是最长回文子串的轴

由上面的这个规律可以知道，我们只需要遍历一遍字符串，将每一个字符（偶数串为两个连续字符）作为轴，寻找最长的回文串，最后这些回文串中最长的即为整个字符串中的最长回文子串。
遍历一遍是n数量级的时间，寻找回文子串也是n数量级，所以时间复杂度是O(n^2)
但是这样问题又来了，偶数串和奇数串的处理方法不同，需要分别处理。这时候我们就要用一个小技巧，用‘#’插入字符串中字符的间隔中，这样就将所有字符串都转换成奇数串，如下：

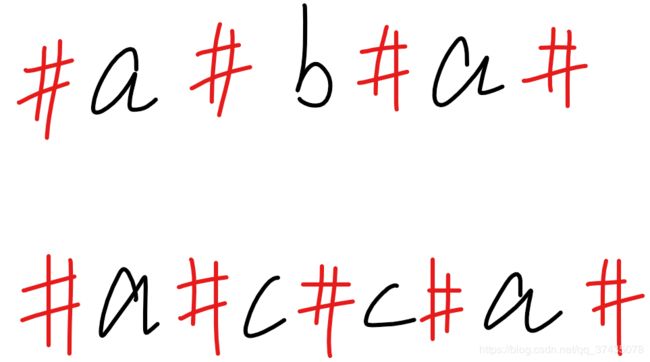
这样我们就可以用一套方法来处理所有的字符串了，而且时间复杂度为O(n^2)。但是我们还要追求更好的算法，这时候就需要更高一级的技术了，接下来就需要介绍一个时间复杂度为n数量级的算法。

Manacher算法

在接下来所要涉及的均为奇数串，首先来介绍以下几个概念：

轴：因为接来下的所有子串都为奇数串，所以轴就确定为一个回文串最中间的字符
半径：一个回文串的轴 左/右边 字符的个数（包括轴），比如aabaa的半径为3，aca的半径为2，c的半径为1。在算法中用 p[i] 表示，i为轴的位置。

再来介绍几个特殊点：

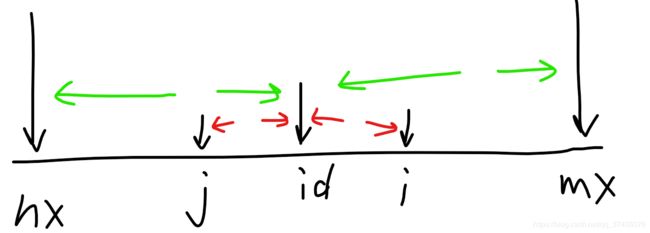
其中，mx是以id为轴的最长回文串的边界，j是i关于id的对称点，nx是mx关于id的对称点。
如果i比mx大的话，那么这个问题就变成了刚才提到的O(n^2)时间复杂度的查找问题，但是假如i比mx小，那么Manacher算法就可以省去很多不必要的检验。
根据回文串的性质很容易得到以下结论：

规律3：
如果nx ~ id区间内存在回文子串，那么id ~ mx同样的位置也会有同样的回文子串

规律4：
p[i] - 1是原字符串中最长回文串的长度

同时为了避免进行越界判别，可以在字符串首位加上两个不会在字符串中出现的不同的字符，比如‘$’和‘\0’，至于为什么选择‘\0’，因为‘\0’本身就是用作截断字符串。

我们遍历的是i，遍历i的时候会发生以下3种情况：

• 以j为轴的回文串在id为轴的回文串内部，简称内部
• 以j为轴的回文串在id为轴的回文串外部，简称外部
• 以j为轴的回文串边界与以id为轴的回文串边界重合，简称重合

对这三种情况进行分类讨论。

内部的情况

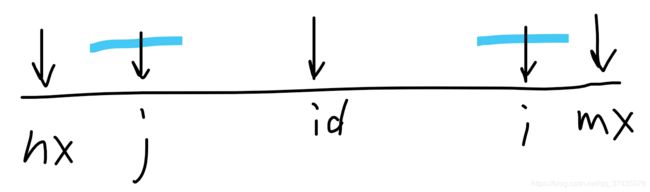
得出的结论是：p[i]=p[j]（不清楚p[i]定义的可以翻到上面重新看半径的定义）。
数学的证明方法这里写起来比较啰嗦，本来这篇文章也不是为了讲解证明过程，以后如果有人有兴趣的话再说，这里简要说明一下证明思路：

假如以i为轴回文串长度加上了橙色的一截，超过了以j为轴的字符串，甚至有可能超过了大回文串时，我们截取这个回文串在大回文串中的一部分，将这段长度对应到轴j上，由规律3可以得知，j轴回文串加上了这一部分长度的新串依然是一个回文串，但是这样的话就与已知条件矛盾（以j为轴回文串的半径为p[j]）。反之，如果p[i]

外部的情况

假如j轴回文串的一部分超过了大回文串，那么i轴回文串的半径就为mx-i，有p[i] = mx - i，如下图：

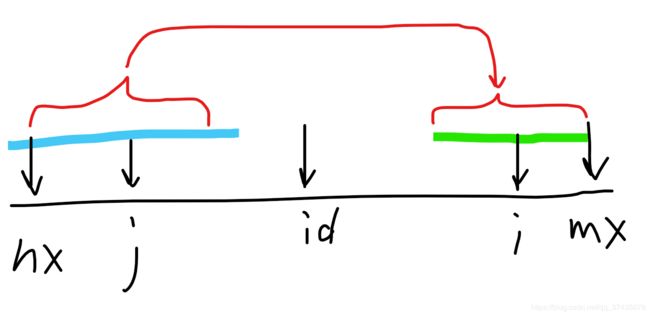
简要证明一下，首先i轴回文串不可能更短，因为图中绿色部分一定是一个回文串（由蓝色部分是回文串和规律3这两个条件可以得出）。然后i轴回文串不可能更长，因为我们已知的条件是id轴回文串最长为nx~mx，那么说明超过这段的串一定不是回文串，那么假如i轴回文串超过了大回文串，由规律3和回文串的性质很容易得到id轴回文串会变得更长，这与已知条件相悖。

重合的情况

假如j轴回文串正好和边界重合，即p[j] = mx - i，那么p[i] >= p[j]，如下图：

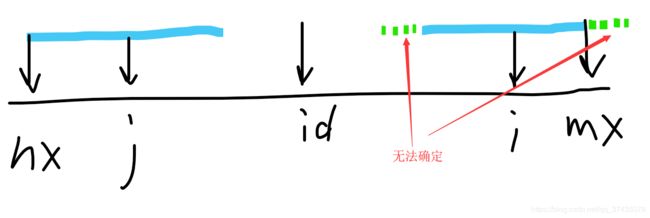
简要证明一下，首先p[i]不可能更小（见规律3），然后需要证明p[i]可能变得更大。我们已知的是j轴回文串正好和大回文串边界重合，我们可以得出以下两个结论

j轴回文串两侧的字符不相等
大回文串两侧的字符不相等

数学上我们学过a ≠ b，b ≠ c，并不能推出a ≠ c，所以i轴回文串两侧的字符是否相等还得进一步判断。

总结

Manacher算法的核心思想就是尽可能找到一个轴id，让mx > i，这样就可以用以上的3种方法来进行快速判别，同时因为整个算法只需要遍历一遍字符串，大回文串是一直在外扩的，并不会进行回退，所以整个算法的时间复杂度为O(n)。

代码实现

		char str[1050];
		str[0] = '$';
		str[1] = '#';

		int len = s.size();
		int sl = 2;	// sl为处理后字符串的长度

		for (int i = 1; i < len; i++)
		{
			str[sl++] = s[i];
			str[sl++] = '#';
		}
		str[sl] = '\0';
		
		int mx = 0, id = 0;
		int p[1050];
		memset(p, 0, sizeof(p));
		int ml = 1;

		for (int i = 1; i < sl; i++)
		{
			if (i < mx)
				p[i] = min(p[2 * id - 1], mx - i);	// 2*id-1即为j的位置
			else	
				p[i] = 1;

			while (str[i - p[i]] == str[i + p[i]]) {
				p[i]++;
			}

			if (mx < i + p[i]) {	// 尽可能找到一个大的id和mx
				id = i;
				mx = i + p[i];
			}

			ml = max(ml, p[i] - 1);	// 更新最大值
		}
		return ml;