R&SPSS重复测量方差分析
最近在做重复测量方差分析,真的是走了很多弯路,足足花费了我两周的时间,因此在此写一篇博文,希望能给其他人提供一些参考。
先说建议:
建议使用SPSS,不要使用R,会省很多精力,我用R做了3天,失败了,然后改用SPSS,花了1天就搞定,一方面是因为SPSS确实对用户很友好,而且很简单,另一方面也是因为SPSS有很多的教程,照着用就行了,很方便。
接下来,我首先介绍我的项目背景吧,我是获得了某月一个城市的车辆数随时间的变化情况,然后我希望比较各天的车辆数有没有显著性差异,所以就做了方差分析。
数据类似于下面这样(部分):
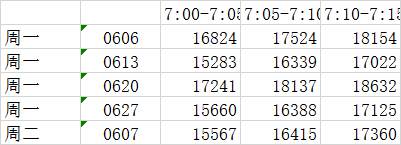
其中‘周x’是一个组间因素,因为每个样本只会做一个处理(这边的样本就是该城市运行的车辆),然后时间(7:00-7:15这些)就是组内因素,因为每个样本都在两个或两个以上的处理下进行了测量,这就是一个十分典型的重复测量方差分析了,然后我这边各个处理的样例数目是不一样的,因此说,我做的是非均衡重复测量方差分析。
前期介绍就到这里啦,如果对重复测量方差分析还有疑问的可以网上查一下,其中对于组间因素和组内因素我参考的是这篇文章:https://wenku.baidu.com/view/d17dc3130b4e767f5acfce33.html
然后结合R语言实战中的方差分析一章节基本搞懂了。
先说明下重复测量方差分析要满足的假设:
使用两因素重复测量方差分析(Two-way Repeated Measures Anova)进行分析时,需要考虑5个假设。
假设1:因变量唯一,且为连续变量;
假设2:有两个受试者内因素(Within-Subject Factor),每个受试者内因素有2个或以上的水平。
注:在重复测量的方差分析模型中,对同一个体相同变量的不同次观测结果被视为一组,用于区分重复测量次数的变量被称为受试者内因素,受试者内因素实际上是自变量。
对数据的假设:
假设3:受试者内因素的各个水平,因变量没有极端异常值;
假设4:受试者内因素的各个水平,因变量需服从近似正态分布;
假设5:对于受试者内因素的各个水平组合而言,因变量的方差协方差矩阵相等,也称为球形假设。
摘自——https://mp.weixin.qq.com/s?__biz=MzI2OTQyMzc5MA==&mid=2247488797&idx=1&sn=34f6d5c3dabf2988b7b85071ebd312f3&chksm=eae1d0dcdd9659ca501644823def4d9d40777939813a381f50f6c1a117863ca6f7eb89bae289&scene=21#wechat_redirect
然后说一下用R做的过程中踩过的一些吭吧:
1、R语言的资料真的很少,所以我基本上都是参考R语言实战来做的,在重复测量方差分析一节直接讲了怎么做重复测量方差分析,但是并没有对数据进行检验,重复测量方差分析一下子就成功做出来了,很简单,但是我看方差分析都是要做检验的,所以我就去网上搜检验的方法。(详见前述的5个假设)
2、知道了要做这些假设后,基本也就明白了最关键的就是球形假设了,而球形假设最常见的就是使用mauchly test,但是网上搜啊搜,就是没搜到这方面的资料,非常尴尬,没办法,只好直接上R的官方文档了,网址如下:
https://www.rdocumentation.org/packages/stats/versions/3.4.1/topics/mauchly.test
然后要看懂这个还需要以下一些文档:
https://www.rdocumentation.org/packages/stats/versions/3.4.1/topics/SSD
https://www.rdocumentation.org/packages/stats/versions/3.4.1/topics/mauchly.test
由于不是学统计的,对立面的一些术语也不是很理解,所以只有依靠官方给的例子了:
# Lifted from Baron+Li:
# "Notes on the use of R for psychology experiments and questionnaires"
# Maxwell and Delaney, p. 497
reacttime <- matrix(c(
420, 420, 480, 480, 600, 780,
420, 480, 480, 360, 480, 600,
480, 480, 540, 660, 780, 780,
420, 540, 540, 480, 780, 900,
540, 660, 540, 480, 660, 720,
360, 420, 360, 360, 480, 540,
480, 480, 600, 540, 720, 840,
480, 600, 660, 540, 720, 900,
540, 600, 540, 480, 720, 780,
480, 420, 540, 540, 660, 780),
ncol = 6, byrow = TRUE,
dimnames = list(subj = 1:10,
cond = c("deg0NA", "deg4NA", "deg8NA",
"deg0NP", "deg4NP", "deg8NP")))
mlmfit <- lm(reacttime ~ 1)
summary(mlmfit)
SSD(mlmfit)
$SSD
cond
cond deg0NA deg4NA deg8NA deg0NP deg4NP deg8NP
deg0NA 29160 30600 26640 23760 32400 25560
deg4NA 30600 66600 32400 7200 36000 30600
deg8NA 26640 32400 56160 41040 57600 69840
deg0NP 23760 7200 41040 70560 72000 63360
deg4NP 32400 36000 57600 72000 108000 100800
deg8NP 25560 30600 69840 63360 100800 122760
$call
lm(formula = reacttime ~ 1)
$df
[1] 9
attr(,"class")
[1] "SSD"
estVar(mlmfit)
cond
cond deg0NA deg4NA deg8NA deg0NP deg4NP deg8NP
deg0NA 3240 3400 2960 2640 3600 2840
deg4NA 3400 7400 3600 800 4000 3400
deg8NA 2960 3600 6240 4560 6400 7760
deg0NP 2640 800 4560 7840 8000 7040
deg4NP 3600 4000 6400 8000 12000 11200
deg8NP 2840 3400 7760 7040 11200 13640
### traditional test of intrasubj. contrasts
mauchly.test(mlmfit, X = ~1)
Mauchly's test of sphericity
Contrasts orthogonal to
~1'
data: SSD matrix from lm(formula = reacttime ~ 1)
W = 0.031084, p-value = 0.04765
### tests using intra-subject 3x2 design
idata <- data.frame(deg = gl(3, 1, 6, labels = c(0,4,8)),
noise = gl(2, 3, 6, labels = c("A","P")))
mauchly.test(mlmfit, X = ~ deg + noise, idata = idata)
Mauchly's test of sphericity
Contrasts orthogonal to
~deg + noise'
data: SSD matrix from lm(formula = reacttime ~ 1)
W = 0.89378, p-value = 0.6381
mauchly.test(mlmfit, M = ~ deg + noise, X = ~ noise, idata = idata)
Mauchly's test of sphericity
Contrasts orthogonal to
~noise
Contrasts spanned by
~deg + noise'
data: SSD matrix from lm(formula = reacttime ~ 1)
W = 0.96011, p-value = 0.8497
简单说明下其中的一些东西吧,输入一个矩阵,一列是一个sample,做一个线性回归,但是这个线性回归~1,其实就是求每一列的均值,形成一个object mlmfit,SSD()函数就是求出一个矩阵,名字叫这玩意:The residual sums of squares and products matrix,我自己翻译为“残差平方和-积和矩阵”也不知对不对,不好意思,没学过这玩意。
estVar(mlmfit)这个函数其实就是求出协方差矩阵啦!然后就可以做球形检验了。
我基本上就是做到这一步,之后就没再做下去了,因为我发现我的例子中不满足球形假设,因此实际上需要做出调整,但是R语言没有给出调整后的值,所以如果坚持要使用R,还需要花费很多时间,所以就放弃了,改用SPSS,因为SPSS可以直接给出球形检验的结果和调整值,十分简单方便。
SPSS的使用在此就不介绍了,因为网上介绍很多很多了,这里推荐两个,写的很好,很完整,大家自己去看大佬写的东西吧:
https://www.sohu.com/a/123940962_489312
https://mp.weixin.qq.com/s?__biz=MzI2OTQyMzc5MA==&mid=2247488797&idx=1&sn=34f6d5c3dabf2988b7b85071ebd312f3&chksm=eae1d0dcdd9659ca501644823def4d9d40777939813a381f50f6c1a117863ca6f7eb89bae289&scene=21#wechat_redirect
不过,用spss我还是遇到了一个坑,在此提醒大家注意下:
如果重复检测次数过多,也就是组内因素time设的过多时,球形检验那一项的sig会是空的,因为无法计算出来。原因是自由度太多了,但是给的样例又太少了,这样就无法计算出结果,遇到这个问题时,需要减少time的检测次数,或是增加样例数,但是一般增加样例数比较难,所以就减少重复检测次数就行啦,然后就可以成功计算出球形检验值啦!
其他应该没什么需要注意的了,希望大家一切顺利。