元启发式算法之一：蝙蝠算法BA

目录

一、算法

1. 定义

2. 步骤

3. 特点

  二、蝙蝠

      1.描述

      2.先进技能-声纳

1） 回声定位-Acoustics of Echolocation

2） 行为参数化分析

     3. 技能属性

三、 蝙蝠算法

1.算法模型建立之规则理想化简化

2.算法模型建立之近似值应用

3.算法模型建立之算法描述

4.算法方程

      5.BA算法步骤的伪代码

        6.算法实现参数之响度和脉冲发射

        7.算法验证

             1）验证新算法的标准函数

            2） 测试实例

      8.MATLAB实现蝙蝠算法可视化

      9.Python代码实现蝙蝠算法

四、总结

五、蝙蝠算法的研究

1.蝙蝠算法关键技术统计

2.蝙蝠算法在性能方面的研究

3.蝙蝠算法的研究应用领域尝试方面的研究

---

一、算法

1. 定义

             特定计算模型的有穷指令序列集合。

2. 步骤

              参数数据输入--步骤1--步骤2--...步骤k...步骤n--结果参数数据输出

3. 特点

• 1.有穷性（Finiteness）：算法的有穷性是指算法必须能在执行有限个步骤之后终止；

• 2.确切性(Definiteness)：算法的每一步骤必须有确切的定义；

• 3.输入项(Input)：一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输入是指算法本身定出了初始条件；

• 4.输出项(Output)：一个算法有一个或多个输出，以反映对输入数据加工后的结果。没有输出的算法是毫无意义的；

• 5.可行性(Effectiveness)：算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步，即每个计算步都可以在有限时间内完成（也称之为有效性）。

  二、蝙蝠

      1.描述

        唯一长着翅膀的[翼手目]哺乳动物，具有敏锐的听觉定向（或回声定位）系统，可以通过喉咙发出超声波然后再依据超声波回应来辨别方向、探测目标的。有一些种类的面部进化出特殊的增加声纳接收的结构，如鼻叶、脸上多褶皱和复杂的大耳朵。许多蝙蝠也有鼻叶，由皮肤和结缔组织构成，围绕着鼻孔或在鼻孔上方拍动。据认为鼻叶影响发声及回声定位。

•        有些蝙蝠的飞行速度可达每小时50千米以上。
•        蝙蝠能在1秒钟内捕捉和分辨250组回音。（注：音波往返一次算一组。）
•        蝙蝠的视力很好，并没有退化。它由嘴发出高出两万赫兹的声波，叫“超声波”，人是听不见的。超声波遇到障碍物就会反射回来，传到蝙蝠的灵敏的耳朵里。蝙蝠通过大脑，判断出障碍物样子等，来判断是吃是逃。

      2.先进技能-声纳

1） 回声定位-Acoustics of Echolocation

       大多数蝙蝠使用短调频信号扫过一个八度音阶;其他的则经常使用恒定频信号进行回声定位。它们的信号带宽随着物种而变化，通常通过使用更多的谐波来增加。蝙蝠使用了回声发射与检测的时延，两耳之间的时间差和回声响度的变化来建立周围环境的三维场景。它们可以侦测到目标的距离和方向，猎物的类型，甚至猎物的移动速度，如小昆虫。研究表明，蝙蝠似乎能够通过目标昆虫的翅膀颤动率引起的多普勒效应的变化来区分目标。

2） 行为参数化分析

                  尽管每个脉冲的持续时间只有千分之几秒（最长可达 8 到 10 ms），但它的频率通常在 25 kHz 到 150 kHz 之间。尽管有些种类的蝙蝠可以发出高达 150 kHz 的高频声波，但大多数蝙蝠的典型频率范围在 25 kHz 到 100 kHz 之间。每个超声波脉冲可以（典型地）持续 5 到 20ms，小蝙蝠每秒可以发出大约 10 到 20 个这样的声波脉冲。当它们捕猎靠近猎物时，脉冲发射速率可以被加速到每秒约 200 个脉冲。这样的短时声音突发意味着蝙蝠具有奇妙的信号处理能力。事实上，研究表明，蝙蝠耳朵的等效积分时间通常约为 300 到 400 微秒。

                   由于空气中室温下声速的典型值为 v=340m/s，所以以恒定频率 f 发出的超声波，其波长 λ 由 λ=v/f给出，其中，典型波长为 2 mm 到 14 mm，典型频率为 25 kHZ 到 150 kHZ。这些波长显然与猎物尺寸在同一数量级[2,27]。

                   蝙蝠发出的脉冲可能高达 110 分贝（dB），幸好脉冲处于超声波区。响度也随着目的不同而改变，从最响的搜寻猎物到相对安静飞向猎物。这种短脉冲的行程范围通常是几米，其取决于实际的频率。小蝙蝠可以设法避免如人头发丝一样薄的障碍物。

     3. 技能属性

1.                 位置：蝙蝠位置xi 和猎物位置x*
2.                 响度：Ai  (影响因素：蝙蝠具有不同的频率或波长、响度)
3.                  脉冲发射率：r 
4.                  飞行速度： vi

三、 蝙蝠算法

蝙蝠算法（Bat Algorithm，BA）是2012年杨教授提出的一种群智能优化算法。该算法具有实现简单、参数少等特点，已经成为近几年启发式算法的研究热点。蝙蝠算法也像其他群智能优化算法一样是一种基于迭代的优化算法。

1.算法模型建立之规则理想化简化

1. 所有的蝙蝠都用回声定位来感知距离，并且“知道”食物/猎物与背景障碍之间的差异。

2. 蝙蝠在位置 xi ，以速度 vi 随机飞行，它们可以自动调整发出脉冲的频率（波长），并依据目标的接近程度调整脉冲发射率r∈[0,1]。

3. 虽然响度可以从多个方面改变，但我们假设响度从一个大（正）值 A0变化到最小值 Amin。

           注：另一个明显的简化是，估计时延和三维地形时不使用射线追踪（ray tracing）。尽管在计算几何应用中这可能是一个很好的特性，但在这里不使用这种简化，因为在多维时增加了计算量。

2.算法模型建立之近似值应用

       通常，频率 f 在范围 [fmin,fmax] 内，相应的波长在范围 [λmin,λmax]内。例如，频率在 [20 kHz, 500 kHz] 范围内，则相应的的波长在 [0.7 mm, 17 mm] 范围内。对于给定的问题，我们可以使用任意波长来实现。在实际应用中，我们可以通过调整频率（波长）来调整范围。选择的范围（或最大波长）应与感兴趣区域的大小相当，然后再逐渐调整至较小的范围。而且，我们不一定必须调节波长本身。相反，可以通过改变频率来实现。这是因为 λ和 f 相关，λf的值是常数。稍后我们给出使用这一方法的实现。为简单起见，可以假设 f∈[0,fmax]。我们知道较高的频率具有短的波长和较短的距离。

       蝙蝠的典型范围是几米。冲发射率可以表示为 [0,1] ，其中 0 表示完全没有脉冲，1 表示最大的脉冲发射率。

3.算法模型建立之算法描述

把蝙蝠的回声定位理想化，可以总结如下：每个虚拟蝙蝠有随机的飞行速度Vi在位置Xi（问题的解），同时蝙蝠具有不同的频率或波长、响度Ai和脉冲发射率r。蝙蝠狩猎和发现猎物时，它改变频率、响度和脉冲发射率，进行最佳解的选择，直到目标停止或条件得到满足。这本质上就是使用调谐技术来控制蝙蝠群的动态行为，平衡调整算法相关的参数，以取得蝙蝠算法的最优。通过对多个标准测试函数的测试，展现了在连续性优化问题中的较好应用。

4.算法方程

在模拟中，我们使用虚拟蝙蝠。需要定义d-维搜索空间虚拟蝙蝠位置 xi 速度 vi 值更新的规则，在时间步长 t 新解 xti 和速度 vti给出如下

fi=fmin+(fmax−fmin)β,(1)

vt+1i=vti+(xti−x∗)fi,(2)

xt+1i=xti+vt+1i,(3)

         其中 β∈[0,1]是服从均匀分布的随机向量。这里 x∗ 是当前全局最佳位置（解），它是在比较了所有 n 个蝙蝠的所有解后找到的。由于乘积 lambdaifi 是一个常数，我们可以使用 fi（或 λi）来调整速度大小，同时固定另一个因子 λi（或 fi），这取决于具体的问题类型。对于我们的实现，使用 fmin=0 和 fmax=O(1)，其取决于感兴趣问题域的大小。开始时，每个蝙蝠被随机分配一个服从均匀分布 [fmin,fmax]的频率。

        对于局部搜索部分，一旦从当前最佳解中选择了一个解，则使用随机游走对每个蝙蝠产生一个新解

xnew=xold+ϵA(t),(4)

       其中 ϵ∈[−1,1] 是一个随机数，而 A(t)=〈Ati〉 是此时间步长中所有蝙蝠的平均响度。从实现的角度来看，最好能够提供一个缩放参数来控制步长。因此，我们可以将这个方程改写为：

xnew=xold+σϵtA(t),(5)

      其中 ϵt 服从高斯正态分布 N(0,1)，σ 是缩放因子。在 demo 中，设置为 σ=0.01。显然，σ 应该与所考虑优化问题的设计变量的尺度相关联。

      蝙蝠速度和位置的更新可能与标准粒子群优化（PSO）程序有些相似，因为 fi本质上控制了粒子群运动的速度和范围。然而，BA 更有效，因为它使用频率调节和参数控制来影响种群的探索发现。

      5.BA算法步骤的伪代码

初始化蝙蝠种群 xi 和 vi (i=1,2,...,n)
初始化频率 fi，脉冲发射率 ri ，和响度 Ai 
while (t < Max 迭代数) 
    通过调整频率产生新解 
    更新速度与位置/解 [公式(1) 到 (3)] 
    if (rand > ri) 
        从最佳解中选择一个  
        围绕选择的解产生一个局部解 
    end if 
    通过随机飞行产生新解 
    if (rand < Ai & f(xi) < f(x*)) 
        接受新解 
        增加 ri 
        减少 Ai 
    end if 
排列蝙蝠，找出当前最佳解 x* 
end while

        6.算法实现参数之响度和脉冲发射

          响度 Ai 和脉冲发射率 ri 也随着迭代的进行而相应地更新。因为一旦发现猎物，响度通常会降低，而脉冲发射率会增加。响度可以为了方便而设置成任意值。为简单起见，可以设 A0=1,Amin=0 ，假设 Amin=0  意味着一只蝙蝠刚刚了找到猎物，暂时停止发声。那么现在我们有

At+1i=αAti,rt+1i=r0i[1−exp(−γt)],(6)

         其中 α 和 γ 是常数。实际上，α 与模拟退火中冷却进度表（cooling schedule ）的冷却因子相似。对于任何 0<α<1 和 γ>0，我们有

Ati→0,rti→r0i,as t→∞.(7)

         在最简单的情况下，可以用 α=γ，在我们的模拟中用了 α=γ=0.9。需要指出的是，演示代码中并不包含 A 和 r 的变化，这里主要是为了说明蝙蝠算法中频率调节的本质。

      参数的选择需要试验。开始时，每只蝙蝠应具有不同的响度和脉冲发射率，这可以通过随机化来实现。例如，初始响度 A0i

通常可以取为 1，初始 发射率 r0i 如果使用（6）式，可以是 0 或任何 r0i∈(0,1]，只有当新解得到改进时，响度和发射率才会更新，这便意味着这些蝙蝠正朝着最优解努力。仔细分析 BA，我们可以发现它可以捕捉到许多其他算法的特征。如果我们用随机参数代替频率 fi并设 Ai=0，ri=1，BA 基本上成为了标准 PSO。同样，如果不使用速度，而使用固定的响度和发射率：Ai 和 ri。例如，Ai=ri=0.7，该算法则简化为简单和声搜索（harmony search, HS），因为频率/波长的变化本质上是音调的调整，而脉冲发射率则类似于 HS 中的谐波接受率。换句话说，HS 和 PSO 可以被认为是 BA 的特例。因此，BA 高效并不奇怪。

        7.算法验证

             1）验证新算法的标准函数

                   新算法在14个标准测试函数和10个CEC 2011现实世界问题上显著优于基本算法。

            2） 测试实例

从伪代码来看，用编程语言实现 BA 都是相对简单的。 为了便于可视化，我们用 Matlab 实现了它。
有许多用于验证新算法的标准测试函数。我们来看看一个简单的基准函数 egg crate 函数
f=x2+y2+25(sinx2+siny2,(x,y)∈[−2π,2π]×[−2π,2π])

       f 在 (0,0) 处有一个全局最小值 fmin=0。在实现中,用了 n = 25 到 50 个虚拟蝙蝠，α=0.9。经过迭代，我们会看到蝙蝠正在向最优解（0,0）努力。

      8.MATLAB实现蝙蝠算法可视化

 

% -------------------------------------------------------- %
 % Bat-inspired algorithm for continuous optimization (demo)% 
 % A 和 r 设为常数以简化蝙蝠算法%
-------------------------------------------------------- % 
function [best,fmin,N_iter]=bat_algorithm(para) 
% Default parameters 
if nargin<1, 
para=[10 0.25 0.5]; 
end n=para(1); 
% Population size, typically 10 to 25 
A=para(2); 
% Loudness (constant or decreasing) 
r=para(3); 
% Pulse rate (constant or decreasing) 
% This frequency range determines the scalings 
Qmin=0; 
% Frequency minimum 
Qmax=2; 
% Frequency 
maximum 
% Iteration parameters 
tol=10^(-5); 
% Stop tolerance 
N_iter=0; 
% Total number of function evaluations 
% Dimension of the search variables 
d=3; 
% Initial 
arrays Q=zeros(n,1); 
% Frequency 
v=zeros(n,d); 
% Velocities 
% Initialize the population/solutions 
for i=1:n 
  Sol(i,:)=randn(1,d); 
  Fitness(i)=Fun(Sol(i,:)); 
end 
% Find the current best 
[fmin,I]=min(Fitness); 
best=Sol(I,:); 
% Start the iterations -- Bat Algorithm 
while (fmin>tol)   
  % Loop over all bats/solutions 
  for i=1:n  
     Q(i)=Qmin+(Qmin-Qmax)*rand; 
     v(i,:)=v(i,:)+(Sol(i,:)-best)*Q(i); 
     S(i,:)=Sol(i,:)+v(i,:); 
  % Pulse rate 
     if rand>r 
        S(i,:)=best+0.01*randn(1,d); 
     end 
  % Evaluate new solutions 
     Fnew=Fun(S(i,:)); 
  % If the solution improves or not too loudness 
    if (Fnew<=Fitness(i)) & (rand

      9.Python代码实现蝙蝠算法

#!/usr/bin/env python3

"""An implementation of Bat Algorithm
"""

import numpy as np
from numpy.random import random as rand

__author__ = "GreatX"
__copyright__ = "Copyright 2017"
__credits___ = ["GreatX"]
__license__ = "MIT"
__email__ = "[email protected]"

# Parameters setting
# objfun: objective function
# N_pop: population size, typically 10 to 40
# N_gen: number of generation
# A: loudness (constant or decreasing)
# r: pulse rate (constant or decreasing)
# This frequency range determines the scalings
# You should change these values if necessary
# Qmin: frequency minmum
# Qmax: frequency maxmum
# d: number of dimensions
# lower: lower bound
# upper: upper bound
def bat_algorithm(objfun, N_pop=20, N_gen=1000, A=0.5, r=0.5,
    Qmin=0, Qmax=2, d=10, lower=-2, upper=2):

    N_iter = 0 # Total number of function evaluations
    # Limit bounds
    Lower_bound = lower * np.ones((1,d))
    Upper_bound = upper * np.ones((1,d))

    Q = np.zeros((N_pop, 1)) # Frequency
    v = np.zeros((N_pop, d)) # Velocities
    S = np.zeros((N_pop, d))

    # Initialize the population/soutions
    # Sol = np.random.uniform(Lower_bound, Upper_bound, (N_pop, d))
    # Fitness = objfun(Sol)
    Sol = np.zeros((N_pop, d))
    Fitness = np.zeros((N_pop, 1))
    for i in range(N_pop):
        Sol[i] = np.random.uniform(Lower_bound, Upper_bound, (1, d))
        Fitness[i] = objfun(Sol[i])

    # Find the initial best solution
    fmin = min(Fitness)
    Index = list(Fitness).index(fmin)
    best = Sol[Index]

    # Start the iterations
    for t in range(N_gen):

        # Loop over all bats/solutions
        for i in range(N_pop):
            # Q[i] = Qmin + (Qmin - Qmax) * np.random.rand
            Q[i] = np.random.uniform(Qmin, Qmax)
            v[i] = v[i] + (Sol[i] - best) * Q[i]
            S[i] = Sol[i] + v[i]
            # Apply simple bounds/limits
            Sol[i] = simplebounds(Sol[i], Lower_bound, Upper_bound)
            # Pulse rate
            if rand() > r:
                # The factor 0.001 limits the step sizes of random walks
                S[i] = best + 0.001*np.random.randn(1, d)

            # Evaluate new solutions
            # print(i)
            Fnew = objfun(S[i])
            # Update if the solution improves, or not too loud
            if (Fnew <= Fitness[i]) and (rand() < A):
                Sol[i] = S[i]
                Fitness[i] = Fnew

            # update the current best solution
            if Fnew <= fmin:
                best = S[i]
                fmin = Fnew

        N_iter = N_iter + N_pop

    print('Number of evaluations: ', N_iter)
    print("Best = ", best, '\n fmin = ', fmin)

    return best


def simplebounds(s, Lower_bound, Upper_bound):

    Index = s > Lower_bound
    s = Index * s + ~Index * Lower_bound
    Index = s < Upper_bound
    s = Index * s + ~Index * Upper_bound

    return s


# u: array-like
def test_function(u):
    a = u ** 2
    return a.sum(axis=0)


if __name__ == '__main__':
    # print(bat_algorithm(test_function))
    bat_algorithm(test_function)
    # l = [1, 2, 3, 4, 5]
    # u = np.array(l)
    # print(test_function(u))
    # lb = np.array([1, 1, 1, 1])
    # ub = np.array([2, 2, 2, 2])
    # s = np.array([0.5, 3, 1.5, 1.5])
    # print(simplebounds(s, lb, ub))

四、总结

      蝙蝠算法的性能测试在一定程度上经过 标准测试函数及CEC现实世界问题上的测试精度和效率上，一般要高于基本算法，其收敛速度更快。且蝙蝠算法已用于工程设计、分类等应用。把蝙蝠算法（BA）与遗传算法（GA）、PSO等方法进行比较，并用于训练神经网络，得出的结论显示：蝙蝠算法比其他算法有很好优势。

五、蝙蝠算法的研究

蝙蝠算法研究大多偏向：如何改善蝙蝠算法的性能方面 和领域应用性尝试方面

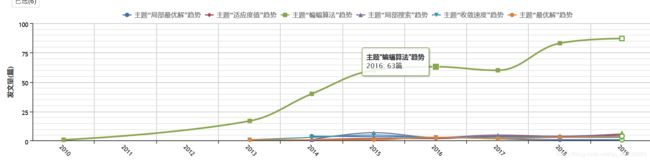
1.蝙蝠算法关键技术统计

蝙蝠算法

2.蝙蝠算法在性能方面的研究

      蝙蝠算法性能主要包括

1. 局部搜索
2. 局部最优解
3. 收敛速度
4. 最优解
5. 适应度值

     等方面的进行性能方面研究文章结合蝙蝠算法文章进行统计分析如下:

3.蝙蝠算法的研究应用领域尝试方面的研究

蝙蝠算法的研究应用领域尝试统计分析如下：

蝙蝠算法相关研究数据统计分析标题

下面是参考引用的部分博主的蝙蝠算法优秀讲解的连接，本文也在学习的基础上，做了适当的统计研究。

参考一：常见测试函数

参考二：GrWx的蝙蝠算法