禁忌搜索算法求解TSP问题python实现
文章目录
- 1 禁忌搜索(Tabu Search)
- 1.1 TS相关术语介绍
- 1.2 算法流程
- 1.3 算例分析
- 2 TS设计
- 2.1 编码原则
- 2.2 数据准备
- 2.3 初始路径的生成
- 2.3.1 随机生成
- 2.3.2 改良圈算法
- 2.3.3 贪婪算法
- 2.4 交换法则
- 2.5 邻域设计
- 2.6 接受准则
- 2.7 新回路的生成
- 2.8 禁忌搜索
- 2.9 绘图
- 3 实验结果分析
- 4 附python源码(完整版)
1 禁忌搜索(Tabu Search)
1.1 TS相关术语介绍
- 邻域
对于组合优化问题,给定任意可行解x,x∈D,D是决策变量的定义域,对于D上的一个映射:N:x∈D→N(x)∈2(D) 其中2(D)表示D的所有子集组成的集合,N(x)成为x的一个邻域,y∈N(x)称为x的一个邻居。
- 候选集合
候选集合一般由邻域中的邻居组成,可以将某解的所有邻居作为候选集合,也可以通过最优提取,也可以随机提取,例如某一问题的初始解是[1,2,3],若通过两两交换法则生成候选集合,则可以是[1,3,2],[2,1,3],[3,2,1]中的一个或几个。
- 禁忌表
禁忌表包括禁忌对象和禁忌长度。由于在每次对当前解的搜索中,需要避免一些重复的步骤,因此将某些元素放入禁忌表中,这些元素在下次搜索时将不会被考虑,这些被禁止搜索的元素就是禁忌对象;
禁忌长度则是禁忌表所能接受的最多禁忌对象的数量,若设置的太多则可能会造成耗时较长或者算法停止,若太少则会造成重复搜索。
- 评价函数
用来评价当前解的好坏,TSP问题中是路径里程。
- 藐视规则
禁忌搜索算法中,迭代的某一步会出现候选集的某一个元素被禁止搜索,但是若解禁该元素,则会使评价函数有所改善,因此我们需要设置一个特赦规则,当满足该条件时该元素从禁忌表中跳出。
- 终止规则
一般当两次迭代得到的局部最优解不再变化,或者两次最优解的评价函数差别不大,或者迭代N次之后停止迭代,通常选择第三种方法。
1.2 算法流程
Step1:生成初始解(随机生成,贪婪算法生成,改良圈算法生成);
Step2:Inversion方法生成邻域;
Step3:更新当前最优解、禁忌表以及下一次进入迭代过程的路径;
Step4:重复Step2~3直到满足程序终止条件(本实验采用迭代次数);
Step5:搜索结果可视化输出。
1.3 算例分析
t a b u _ s i z e = 2 tabu\_size=2 tabu_size=2(禁忌表长)
S 1 = [ 2 , 1 , 4 , 3 ] S_1=[2,1,4,3] S1=[2,1,4,3],$ f(S_1) = 500 , , ,tabu_list =[] , , ,S_0 = [2,1,4,3],best_so_far=500$
随机交换 S 0 S_0 S0中两个元素的位置,一共不重复地交换M(候选集合长度)次
| 交换元素 | 候选集合(邻域) | 目标函数值 |
|---|---|---|
| (2 , 1) | [1,2,3,4] | 480 |
| (1 , 4) | [2,4,1,3] | 436 |
| (4 , 3) | [2,1,3,4] | 652 |
对 S 0 S_0 S0交换1和4时目标函数值最优,此时 S 2 = [ 2 , 4 , 1 , 3 ] S_2=[2,4,1,3] S2=[2,4,1,3], f ( S 2 ) = 436 f(S_2)=436 f(S2)=436。将(1,4)添加到禁忌表中, t a b u _ l i s t = [ ( 1 , 4 ) ] tabu\_list=[(1,4)] tabu_list=[(1,4)],令 S 0 = S 2 , b e s t _ s o _ f a r = 436 S_0=S_2,best\_so\_far=436 S0=S2,best_so_far=436。随机交换 S 2 S_2 S2中两个元素的位置,总共不重复地交换M次
| 交换元素 | 候选集合(邻域) | 目标函数值 |
|---|---|---|
| (2 , 4) | [4,2,1,3] | 460 |
| (4 , 1) | [2,1,4,3] | 500 |
| (1 , 3) | [2,4,3,1] | 608 |
对 S 2 S_2 S2交换2和4时目标函数值最优,此时 S 3 = [ 4 , 2 , 1 , 3 ] S_3=[4,2,1,3] S3=[4,2,1,3], S 0 S_0 S0和 b e s t _ s o _ f a r best\_so\_far best_so_far保持不变 f ( S 3 ) = 460 f(S_3)=460 f(S3)=460。将(2,4)添加到禁忌表中, t a b u _ l i s t = [ ( 1 , 4 ) , ( 2 , 4 ) ] tabu\_list=[(1,4),(2,4)] tabu_list=[(1,4),(2,4)]。随机交换S2中两个元素的位置,总共不重复地交换M次。
| 交换元素 | 候选集合(邻域) | 目标函数值 |
|---|---|---|
| (4 , 2) | [2,4,1,3] | 436 |
| (2 , 1) | [4,1,2,3] | 440 |
| (1 , 3) | [4,2,3,1] | 632 |
对 S 3 S_3 S3交换4和2时目标函数最优,虽然(2,4)已经在禁忌表中,但是 f ( S 3 ) = 436 < b e s t _ s o _ f a r = 460 f(S_3)=436
2 TS设计
2.1 编码原则
采用自然数编码,每一个城市用唯一的一个自然数表示。
如【1、2、3、4、5、6、7】表示7个城市的编号
2.2 数据准备
- 从txt文档中录入城市信息(城市编号及其坐标)
filename = '算例\\eil101.txt'
city_num = [] #城市编号
city_location = [] #城市坐标
with open(filename, 'r') as f:
datas = f.readlines()[6:-1]
for data in datas:
data = data.split()
city_num.append(int(data[0]))
x = float(data[1])
y = float(data[2])
city_location.append((x,y))#城市坐标
- 程序需要使用到的常数
city_count = len(city_num) #总的城市数
origin = 1 #起点和终点城市
remain_cities = city_num[:]
remain_cities.remove(origin) #迭代过程中变动的城市
remain_count = city_count - 1
- 计算城市距离的邻接矩阵,距离采用欧式距离
dis =[[0]*city_count for i in range(city_count)] #初始化
for i in range(city_count):
for j in range(city_count):
if i != j:
dis[i][j] = math.sqrt((city_location[i][0]-city_location[j][0])**2 + (city_location[i][1]-city_location[j][1])**2)
else:
dis[i][j] = 0
- 计算路径的里程成本
def route_mile_cost(route):
'''
:param route:运行路线
'''
mile_cost = 0.0
mile_cost += dis[origin-1][route[0]-1]#从起始点开始
for i in range(remain_count-1):#路径的长度
mile_cost += dis[route[i]-1][route[i+1]-1]
mile_cost += dis[route[-1]-1][origin-1] #到终点结束
return mile_cost
2.3 初始路径的生成
2.3.1 随机生成
输入需要调整位置的城市序列,使用random库中的shuffle方法随机排列,输出初始路径及其对应的里程。
def random_initial_route(remain_cities):
'''
随机生成初始路径
'''
initial_route = remain_cities[:]
random.shuffle(initial_route)
mile_cost = route_mile_cost(initial_route)
return initial_route,mile_cost
2.3.2 改良圈算法
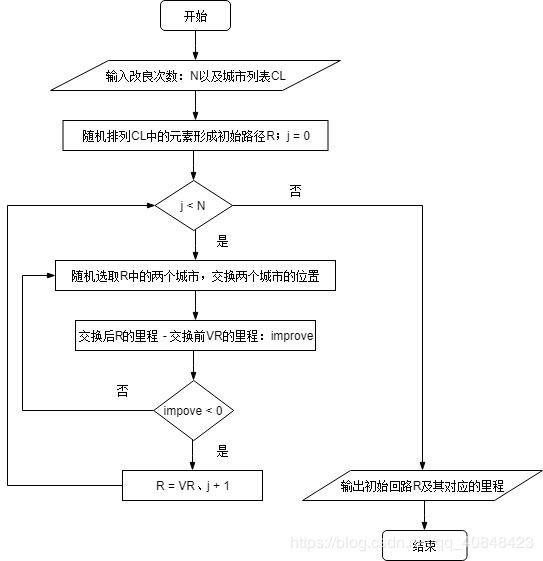
先随机生成路径R如【1、5、6、4、2、3、7、1】形成一个Hamilton圈。随机交换两个点(起点和终点除外)的位置,若交换后路径CR的里程小于交换前路径R的里程,则接受此次交换,令R = CR,否则重新交换,直到成功交换次数达到设置的改良次数。
例1:回路 R = V 1 V 2 ⋯ V i − 1 V i V i + 1 ⋯ V j − 1 V j V j + 1 ⋯ V n V 1 R = V_1V_2\cdots V_{i-1}V_{i}V_{i+1}\cdots V_{j-1}V_{j}V_{j+1}\cdots V_nV_1 R=V1V2⋯Vi−1ViVi+1⋯Vj−1VjVj+1⋯VnV1
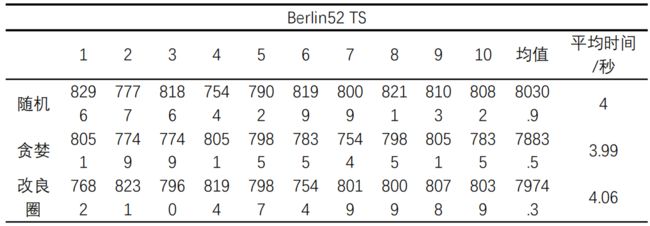
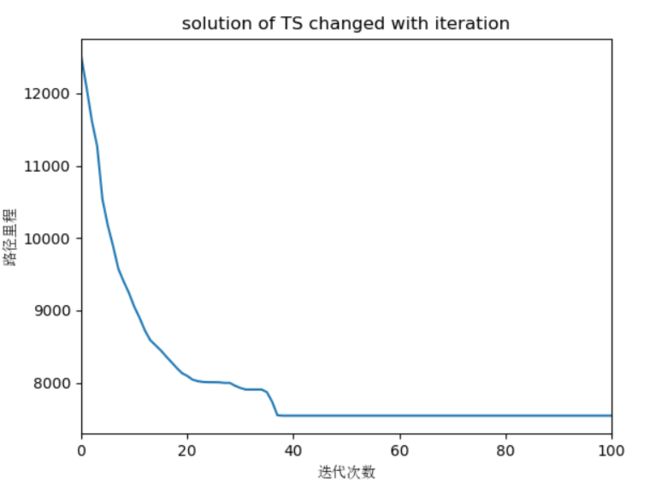
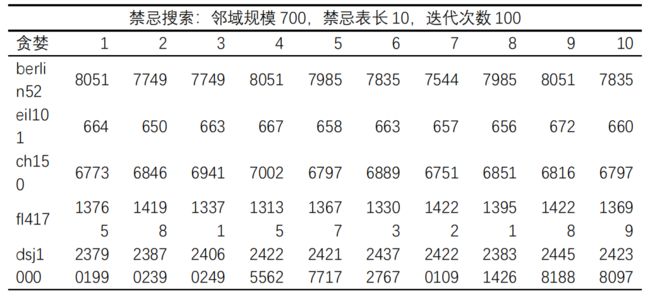
随机选取两个点的位置 ( i , j ) (i,j) (i,j),(1 若有 回路 R = V 1 V 2 ⋯ V i − 1 V j V i + 1 ⋯ V j − 1 V i V j + 1 ⋯ V n V 1 R = V_1V_2\cdots V_{i-1}V_{j}V_{i+1}\cdots V_{j-1}V_{i}V_{j+1}\cdots V_nV_1 R=V1V2⋯Vi−1VjVi+1⋯Vj−1ViVj+1⋯VnV1 ==注:==d表示城市之间的距离矩阵 例2:现有当前回路如下 随机选取两个点如(6,3) 交换两个点的位置并将两点之间的数据倒置 算法思想:从当前城市CR出发找寻与其距离最短的城市NR并标记,令CR=NR,然后继续找寻与CR距离最近的城市并标记,直到所有城市被标记完。最后回到起点城市。 对当前回路R随机选取两个点,倒置两点之间所有点的顺序,形成候选回路cand_route 例:当前回路R =【1、5、6、4、2、3、7、1】,随机选取的两个点如【3,5】 则交换后的回路为: 设置邻域规模candiate_routes_size = 700,表示邻域中能够容纳700条候选路径。 设置交换元素集合canidate_swap存储每次的换方式确保当前路径的邻域中无重复路径。 设置cand_mile_cost存储邻域中回路对应的里程。 流程图: 将邻域中的路径按照里程大小升序排列。当前禁忌表如下 1、破禁法则:若邻域中的最优路径MR不差于当前最优路径CBR,即使MR对应的交换方式S已经存在禁忌表中,仍然接受其成为新的回路。令CBR = MR,并调整S在禁忌表中的位置 例:MR对应的S=【2,4】 调整S到禁忌表的末尾: 2、邻域中的最优路径MR不差于当前最优路径CBR。若MR对应的交换方式S未在禁忌表中,则令CBR = MR,并将其交换方式S添加到禁忌表中。反之,采用破禁法则。 例:MR对应的S = 【2,6】未在当前禁忌表中,将【2,6】添加到禁忌表中。 3、邻域中的最优路径劣于当前最优路径CBR。则选取升序排列的邻域路径中第一个交换方式S未在禁忌表中的路径LR。并将其交换方式S添加到禁忌表中。(==注:==选取的路径最多是邻域中的第tabu_size+1位) 例:邻域中的路径R1,R2,R3虽然都比R4更优,但是前三者对应的交换方式都已经存在禁忌表中,所以选择第一个交换方式未在禁忌表中的R4 邻域路径降序排列: 邻域路径对应的交换方式: 领域设计和接受准则都是为了生成新的路径,因此可以将两者结合放在一个函数中。 以算例berlin52为例,说明初始解对禁忌搜索算法的影响。 初始解分别采用随机生成,贪婪算法,改良圈算法三种方法各自进行10组实验,得出数据如下: 实验结果分析一: 贪婪算法和改良圈算法形成的初始解进行禁忌搜索的结果优于随机生成初始解的结果,并且在这10次实验中GTS的均值显著优于RTS,可见初始解对TS的最终效果有较大影响。此外,ITS虽然同样能够求得最优解,但是耗费的时间要多于RTS和GTS,这是因为改良圈算法的效率受改良次数的影响,如果要得到一个较好的初始解就需要增大改良次数。在初始解生成时间方面,改良圈算法并无优势。 以下是本次实验三种初始解生成方法下的禁忌搜索最优路径及其对应的迭代过程结果。 迭代过程图: 实验结果分析二: 从以上三幅迭代流程图可以看出,禁忌搜索的收敛效率比较高,此外贪婪算法和改良圈算法形成初始解的情况下,TS的迭代过程都有一个缓冲平台。若迭代次数过少,则很容易陷入局部最优(即使随机生成初始解的情况也无例外)。 初始解采用贪婪算法对数据源:berlin52、eil101、ch150、fl417、dsj1000进行TS搜索求解 结果分析:小规模情况下150个数据点以内,TS搜索结果比较理想,gap值在5%以下。随着数据点数的增大,TS搜索结果越偏离最优解(gap值增大)。
d R i − 1 R j + d R j R i + 1 + d R j − 1 R i + d R i R j + 1 < d R i − 1 R i + d R i R i + 1 + d R j − 1 R j + d R j R j + 1 d_{R_{i-1}R_j}+d_{R_{j}R_{i+1}}+d_{R_{j-1}R_i}+d_{R_{i}R_{j+1}}<\\ d_{R_{i-1}R_i}+d_{R_{i}R_{i+1}}+d_{R_{j-1}R_j}+d_{R_{j}R_{j+1}} dRi−1Rj+dRjRi+1+dRj−1Ri+dRiRj+1<dRi−1Ri+dRiRi+1+dRj−1Rj+dRjRj+1
则接受此次交换改良。


improve_count = 100 #改良次数
def improve_circle(remain_cities):
'''
改良圈算法生成初始路径
'''
initial_route = remain_cities[:]
random.shuffle(initial_route)
cost0 = route_mile_cost(initial_route)
route = [1] + initial_route + [1]
label = list(i for i in range(1,len(remain_cities)))
j = 0
while j < improve_count:
new_route = route[:]
index0,index1 = random.sample(label,2)
new_route[index0],new_route[index1]= new_route[index1],new_route[index0]
cost1 = route_mile_cost(new_route[1:-1])
improve = cost1 - cost0
if improve < 0: #交换两点后有改进
route = new_route[:]
cost0 = cost1
j += 1
else:
continue
initial_route = route[1:-1]
return initial_route,cost0
2.3.3 贪婪算法
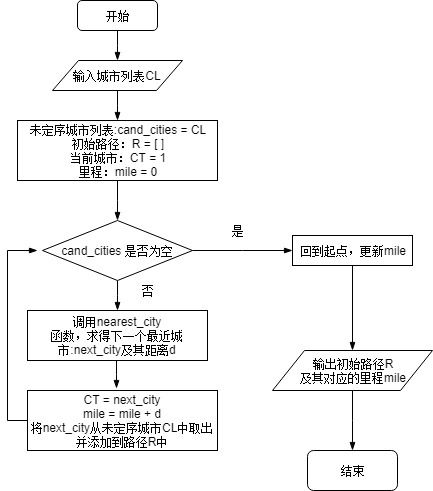
def nearest_city(current_city,cand_cities):
'''
找寻离当前城市最近的城市
'''
temp_min = float('inf')
next_city = None
for i in range(len(cand_cities)):
distance = dis[current_city-1][cand_cities[i]-1]
if distance < temp_min:
temp_min = distance
next_city = cand_cities[i]
return next_city,temp_min
def greedy_initial_route(remain_cities):
'''
采用贪婪算法生成初始解从第一个城市出发找寻与其距离最短的城市并标记,
然后继续找寻与第二个城市距离最短的城市并标记,直到所有城市被标记完。
最后回到第一个城市(起点城市)
'''
cand_cities = remain_cities[:]
current_city = origin
mile_cost = 0
initial_route = []
while len(cand_cities) > 0:
next_city,distance = nearest_city(current_city,cand_cities) #找寻最近的城市及其距离
mile_cost += distance
initial_route.append(next_city) #将下一个城市添加到路径列表中
current_city = next_city #更新当前城市
cand_cities.remove(next_city) #更新未定序的城市
mile_cost += dis[initial_route[-1]-1][0] #回到起点
return initial_route,mile_cost
2.4 交换法则


def random_swap_2_city(route):
'''
随机交换两个城市,并计算里程成本
'''
new_route = route[:]
swap_2_city = random.sample(route,2)
index = [0]*2
index[0] = route.index(swap_2_city[0])
index[1] = route.index(swap_2_city[1])
index = sorted(index)
swap_route = [0]*len(route)
if index[0] != 0:
new_route[index[0]:index[1]+1] = route[index[1]:index[0]-1:-1]
else:
swap_route[0] = route[0]
swap_route[1:index[1]+1] = route[index[1]:0:-1]
swap_route[index[1]+1:] = route[index[1]+1:]
new_route = swap_route[:]
return new_route,sorted(swap_2_city)
2.5 邻域设计
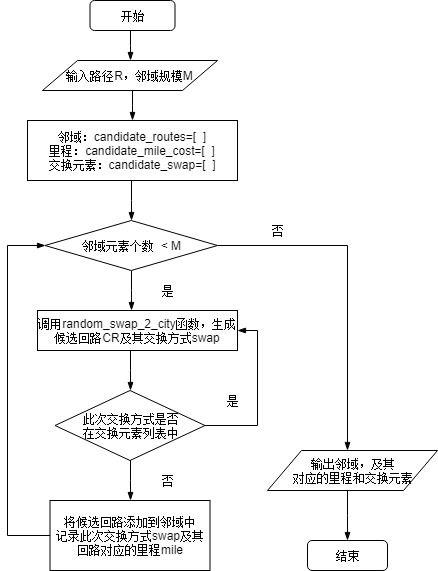
2.6 接受准则

![]()
![]()
![]()


2.7 新回路的生成
def generate_new_route(route):
'''
生成新的路线
'''
global tabu_list,best_so_far_cost,best_so_far_route
global candiate_routes_size,tabu_size
candidate_routes = [] #路线候选集合
candidate_mile_cost = [] #候选集合路线对应的里程成本
candidate_swap = [] #交换元素
while len(candidate_routes) < candiate_routes_size:
cand_route,cand_swap = random_swap_2_city(route)
if cand_swap not in candidate_swap: #此次生成新路线的过程中,没有被交换过
candidate_routes.append(cand_route)
candidate_swap.append(cand_swap)
candidate_mile_cost.append(route_mile_cost(cand_route))
min_mile_cost = min(candidate_mile_cost)
i = candidate_mile_cost.index(min_mile_cost)
#如果此次交换集的最优值比历史最优值更好,则更新历史最优值和最优路线
if min_mile_cost < best_so_far_cost:
best_so_far_cost = min_mile_cost
best_so_far_route = candidate_routes[i]
new_route = candidate_routes[i]
if candidate_swap[i] in tabu_list:
tabu_list.remove(candidate_swap[i]) #藐视法则
elif len(tabu_list) >= tabu_size:
tabu_list.remove(tabu_list[0])
tabu_list.append(candidate_swap[i])
else:
#此次交换集未找到更优路径,则选择交换方式未在禁忌表中的次优
K = candiate_routes_size
stop_value = K - len(tabu_list) - 1
while K > stop_value:
min_mile_cost = min(candidate_mile_cost)
i = candidate_mile_cost.index(min_mile_cost)
#如果此次交换集的最优值比历史最优值更好,则更新历史最优值和最优路线
if min_mile_cost < best_so_far_cost:
best_so_far_cost = min_mile_cost
best_so_far_route = candidate_routes[i]
new_route = candidate_routes[i]
if candidate_swap[i] in tabu_list:
tabu_list.remove(candidate_swap[i]) #藐视法则
elif len(tabu_list) >= tabu_size:
tabu_list.remove(tabu_list[0])
tabu_list.append(candidate_swap[i])
break
else:
#此次交换集未找到更优路径,则选择交换方式未在禁忌表中的次优
if candidate_swap[i] not in tabu_list:
tabu_list.append(candidate_swap[i])
new_route = candidate_routes[i]
if len(tabu_list) > tabu_size:
tabu_list.remove(tabu_list[0])
break
else:
candidate_mile_cost.remove(min_mile_cost)
candidate_swap.remove(candidate_swap[i])
candidate_routes.remove(candidate_routes[i])
K -= 1
return new_route
2.8 禁忌搜索
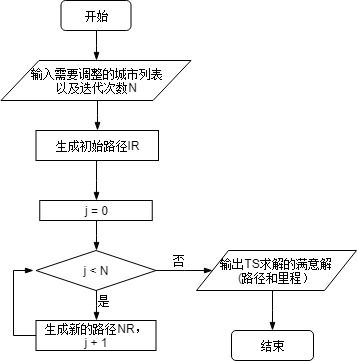
def tabu_search(remain_cities,iteration_count=100):
global tabu_list,best_so_far_cost,best_so_far_route
best_so_far_route,best_so_far_cost = greedy_initial_route(remain_cities)#贪婪算法生成初始解
# best_so_far_route,best_so_far_cost = random_initial_route(remain_cities)#随机生成初始解
#best_so_far_route,best_so_far_cost = improve_circle(remain_cities)#改良圈算法生成初始解
new_route = best_so_far_route[:]
#生成邻域空间
for j in range(iteration_count):
new_route = generate_new_route(new_route)
#输出最终搜索结果
final_route = [origin] + best_so_far_route +[origin]
return final_route,best_so_far_cost
2.9 绘图
def main():
time_start = time.time()
N = 100 #迭代次数
satisfactory_solution,mile_cost,record = tabu_search(remain_cities,N)
time_end = time.time()
print('time cost:',(time_end - time_start))
print("优化里程成本:%d" %(int(mile_cost)))
print("优化路径:\n",satisfactory_solution)
#绘制路线图
X = []
Y = []
for i in satisfactory_solution:
x = city_location[i-1][0]
y = city_location[i-1][1]
X.append(x)
Y.append(y)
plt.plot(X,Y,'-o')
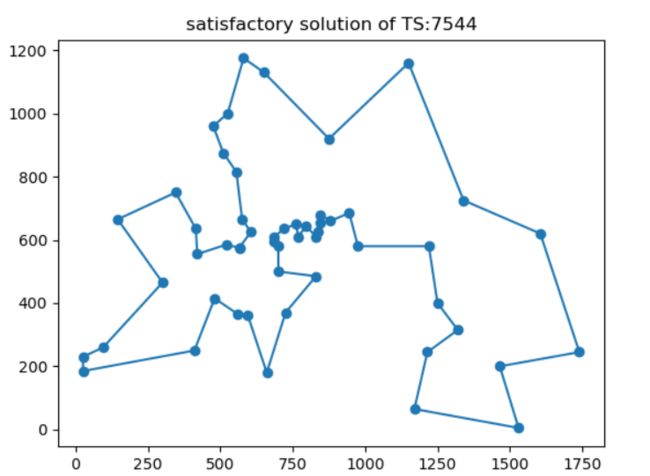
plt.title("satisfactory solution of TS:%d"%(int(mile_cost)))
plt.show()
#绘制迭代过程图
A = [i for i in range(N+1)]#横坐标
B = record[:] #纵坐标
plt.xlim(0,N)
# plt.ylim(7500,record[0])
plt.xlabel('迭代次数',fontproperties="SimSun")
plt.ylabel('路径里程',fontproperties="SimSun")
plt.title("solution of TS changed with iteration")
plt.plot(A,B,'-')
plt.show()
if __name__ == '__main__':
main()
3 实验结果分析


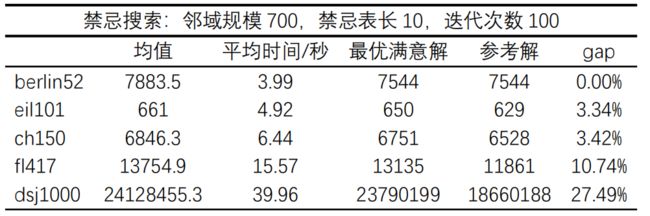
4 附python源码(完整版)
import math,random,time
import matplotlib.pyplot as plt
#读取坐标文件
filename = '算例\\berlin52.txt'
city_num = [] #城市编号
city_location = [] #城市坐标
with open(filename, 'r') as f:
datas = f.readlines()[6:-1]
for data in datas:
data = data.split()
city_num.append(int(data[0]))
x = float(data[1])
y = float(data[2])
city_location.append((x,y))#城市坐标
city_count = len(city_num) #总的城市数
origin = 1 #设置起点和终点城市
remain_cities = city_num[:]
remain_cities.remove(origin) #迭代过程中变动的城市
remain_count = city_count - 1
#计算邻接矩阵
dis =[[0]*city_count for i in range(city_count)] #初始化
for i in range(city_count):
for j in range(city_count):
if i != j:
dis[i][j] = math.sqrt((city_location[i][0]-city_location[j][0])**2 + (city_location[i][1]-city_location[j][1])**2)
else:
dis[i][j] = 0
def route_mile_cost(route):
'''
计算路径的里程
'''
mile_cost = 0.0
mile_cost += dis[origin-1][route[0]-1]#从起始点开始
for i in range(remain_count-1):#路径的长度
mile_cost += dis[route[i]-1][route[i+1]-1]
mile_cost += dis[route[-1]-1][origin-1] #到终点结束
return mile_cost
def random_initial_route(remain_cities):
'''
随机生成初始路径
'''
initial_route = remain_cities[:]
random.shuffle(initial_route)
mile_cost = route_mile_cost(initial_route)
return initial_route,mile_cost
improve_count = 100 #改良次数
def improve_circle(remain_cities):
'''
改良圈算法生成初始路径
'''
initial_route = remain_cities[:]
random.shuffle(initial_route)
cost0 = route_mile_cost(initial_route)
route = [1] + initial_route + [1]
label = list(i for i in range(1,len(remain_cities)))
j = 0
while j < improve_count:
new_route = route[:]
#随机交换两个点
index0,index1 = random.sample(label,2)
new_route[index0],new_route[index1]= new_route[index1],new_route[index0]
cost1 = route_mile_cost(new_route[1:-1])
improve = cost1 - cost0
if improve < 0: #交换两点后有改进
route = new_route[:]
cost0 = cost1
j += 1
else:
continue
initial_route = route[1:-1]
return initial_route,cost0
#获取当前邻居城市中距离最短的1个
def nearest_city(current_city,cand_cities):
temp_min = float('inf')
next_city = None
for i in range(len(cand_cities)):
distance = dis[current_city-1][cand_cities[i]-1]
if distance < temp_min:
temp_min = distance
next_city = cand_cities[i]
return next_city,temp_min
def greedy_initial_route(remain_cities):
'''
采用贪婪算法生成初始解。从第一个城市出发找寻与其距离最短的城市并标记,
然后继续找寻与第二个城市距离最短的城市并标记,直到所有城市被标记完。
最后回到第一个城市(起点城市)
'''
cand_cities = remain_cities[:]
current_city = origin
mile_cost = 0
initial_route = []
while len(cand_cities) > 0:
next_city,distance = nearest_city(current_city,cand_cities) #找寻最近的城市及其距离
mile_cost += distance
initial_route.append(next_city) #将下一个城市添加到路径列表中
current_city = next_city #更新当前城市
cand_cities.remove(next_city) #更新未定序的城市
mile_cost += dis[initial_route[-1]-1][0] #回到起点
return initial_route,mile_cost
def random_swap_2_city(route):
'''
随机选取两个城市并将这两个城市之间的点倒置,计算其里程成本
'''
new_route = route[:]
swap_2_city = random.sample(route,2)
index = [0]*2
index[0] = route.index(swap_2_city[0])
index[1] = route.index(swap_2_city[1])
index = sorted(index)
L = index[1] - index[0] + 1
for j in range(L):
new_route[index[0]+j] = route[index[1]-j]
return new_route,sorted(swap_2_city)
candiate_routes_size = 700 #邻域规模
tabu_size = 10
tabu_list = [] #禁忌表
def generate_new_route(route):
'''
生成新的路线
'''
global tabu_list,best_so_far_cost,best_so_far_route
global candiate_routes_size,tabu_size
candidate_routes = [] #路线候选集合
candidate_mile_cost = [] #候选集合路线对应的里程成本
candidate_swap = [] #交换元素
while len(candidate_routes) < candiate_routes_size:
cand_route,cand_swap = random_swap_2_city(route)
if cand_swap not in candidate_swap: #此次生成新路线的过程中,没有被交换过
candidate_routes.append(cand_route)
candidate_swap.append(cand_swap)
candidate_mile_cost.append(route_mile_cost(cand_route))
min_mile_cost = min(candidate_mile_cost)
i = candidate_mile_cost.index(min_mile_cost)
#如果此次交换集的最优值比历史最优值更好,则更新历史最优值和最优路线
if min_mile_cost < best_so_far_cost:
best_so_far_cost = min_mile_cost
best_so_far_route = candidate_routes[i]
new_route = candidate_routes[i]
if candidate_swap[i] in tabu_list:
tabu_list.remove(candidate_swap[i]) #藐视法则
elif len(tabu_list) >= tabu_size:
tabu_list.remove(tabu_list[0])
tabu_list.append(candidate_swap[i])
else:
#此次交换集未找到更优路径,则选择交换方式未在禁忌表中的次优
K = candiate_routes_size
stop_value = K - len(tabu_list) - 1
while K > stop_value:
min_mile_cost = min(candidate_mile_cost)
i = candidate_mile_cost.index(min_mile_cost)
#如果此次交换集的最优值比历史最优值更好,则更新历史最优值和最优路线
if min_mile_cost < best_so_far_cost:
best_so_far_cost = min_mile_cost
best_so_far_route = candidate_routes[i]
new_route = candidate_routes[i]
if candidate_swap[i] in tabu_list:
tabu_list.remove(candidate_swap[i]) #藐视法则
elif len(tabu_list) >= tabu_size:
tabu_list.remove(tabu_list[0])
tabu_list.append(candidate_swap[i])
break
else:
#此次交换集未找到更优路径,则选择交换方式未在禁忌表中的次优
if candidate_swap[i] not in tabu_list:
tabu_list.append(candidate_swap[i])
new_route = candidate_routes[i]
if len(tabu_list) > tabu_size:
tabu_list.remove(tabu_list[0])
break
else:
candidate_mile_cost.remove(min_mile_cost)
candidate_swap.remove(candidate_swap[i])
candidate_routes.remove(candidate_routes[i])
K -= 1
return new_route,best_so_far_cost
def tabu_search(remain_cities,iteration_count=100):
global tabu_list,best_so_far_cost,best_so_far_route
#生成初始解
best_so_far_route,best_so_far_cost = greedy_initial_route(remain_cities)
# best_so_far_route,best_so_far_cost = random_initial_route(remain_cities)
# best_so_far_route,best_so_far_cost = improve_circle(remain_cities)
record = [best_so_far_cost] #记录每一次搜索后的最优值
new_route = best_so_far_route[:]
#生成邻域
for j in range(iteration_count):
new_route,best_so_far_cost = generate_new_route(new_route)
record.append(best_so_far_cost)
final_route = [origin] + best_so_far_route +[origin]
return final_route,best_so_far_cost,record
def main():
N = 100 #迭代次数
time_start = time.time()
satisfactory_solution,mile_cost,record = tabu_search(remain_cities,N)
time_end = time.time()
time_cost = time_end - time_start
print('time cost:',time_cost)
print("优化里程成本:%d" %(int(mile_cost)))
print("优化路径:\n",satisfactory_solution)
#绘制路线图
X = []
Y = []
for i in satisfactory_solution:
x = city_location[i-1][0]
y = city_location[i-1][1]
X.append(x)
Y.append(y)
plt.plot(X,Y,'-o')
plt.title("satisfactory solution of TS:%d"%(int(mile_cost)))
plt.show()
#绘制迭代过程图
A = [i for i in range(N+1)]#横坐标
B = record[:] #纵坐标
plt.xlim(0,N)
plt.xlabel('迭代次数',fontproperties="SimSun")
plt.ylabel('路径里程',fontproperties="SimSun")
plt.title("solution of TS changed with iteration")
plt.plot(A,B,'-')
plt.show()
return int(mile_cost),time_cost
if __name__ == '__main__':
main()
# M = 10
# Mcosts = [0]*M
# Tcosts = [0]*M
# for j in range(M):
# Mcosts[j],Tcosts[j] = main()
# AM = sum(Mcosts)/M #平均里程
# AT = sum(Tcosts)/M #平均时间
# print("最小里程:",min(Mcosts))
# print("平均里程:",AM)
# print('里程:\n',Mcosts)
# print("平均时间:",AT)