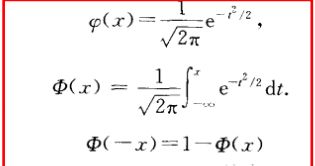概率论与数理统计(二)
m@[toc]
第二章 随机变量及其概率分布
1、随机变量
定义:设随机试验的样本空间为S={e},X=X{e}是定义在样本空间S上的实值单值函数.称X=X{e}为随机变量
常用 ξ , η , ζ \xi,\eta,\zeta ξ,η,ζ希腊字母或X,Y,Z表示
有离散型和连续型
若随机变量只可能取有限个或无限个值时,称之为 离散型随机变量
若随机变量取一个区间内所有实数时,称之为 连续型随机变量
随机变量取值由随机试验的结果确定
随机变量X取某个值x的事件用记号{X=x}表示,其概率即P{X=x}
一般,若L是实数集,将随机变量x在L上的取值事件记为{x ∈ \in ∈L}
其概率记为P{x ∈ \in ∈L}
P{x ∈ \in ∈L}=P{e|X(e) ∈ \in ∈L}
2、离散型随机变量及其分布律
若随机变量只可能取有限个或可数(可列)无限个值时,则称之为离散型随机变量
离散型随机变量X的所有可能取的值为 x k ( k = 1 , 2 , . . . ) x_k(k=1,2,...) xk(k=1,2,...),X取各个可能值的概率,即事件{X= x k x_k xk}的概率,为
P{X= x k x_k xk}= p k p_k pk,k=1,2,…
由概率的定义, p k p_k pk满足如下两个条件:
1.非负性, p k p_k pk ≥ \geq ≥ 0,k=1,2,…
2.规范性, ∑ k = 1 ∞ p k = 1 \sum_{k=1}^{\infty}p_k=1 ∑k=1∞pk=1,所有概率相加为1
以下是三个重要的离散型随机变量
(一)0-1分布
定义:设随机变量X只可能取0和1两个值,它的分布律是
P{X=k}= P k ( 1 − P ) 1 − k , k = 0 , 1 ( 0 < P < 1 ) P^k(1-P)^{1-k},k=0,1(0<P<1) Pk(1−P)1−k,k=0,1(0<P<1)
则称X服从以P为参数的(0-1)分布或两点分布
(二)伯努利试验、二项分布
设试验E只有两种可能结果:A和 A ‾ \overline{A} A,则称E为伯努利试验,设P(A)=p(1
P{X=k}= C n k p k ( 1 − p ) n − k , k = 0 , 1 , 2 , 3... C_n^k p^k(1-p)^{n-k},k=0,1,2,3... Cnkpk(1−p)n−k,k=0,1,2,3...
则称随机变量X服从参数为n,p的二项分布,并记为X~B(n,p)
Q
(三)泊松分布
设随机变量X所有可能取的值为0,1,2,…而取各个值的概率为
P{X=k}= λ k e − λ k ! , k = 0 , 1 , 2 , 3... \frac{\lambda^ke^{-\lambda}}{k!},k=0,1,2,3... k!λke−λ,k=0,1,2,3...
其中 λ \lambda λ>0是常数,则称X服从参数为 λ \lambda λ的泊松分布,记为X~P( λ \lambda λ)
泊松定理:设 λ \lambda λ>0是一个常数,n是任意正整数,设 n p n = λ np_n=\lambda npn=λ,则对于任一固定的非负整数k,有
lim n → ∞ C n k p n k ( 1 − p n ) n − k = λ k e − λ k ! \lim\limits_{n\rightarrow \infty} C_n^k p_n^k(1-p_n)^{n-k}=\frac{\lambda^ke^{-\lambda}}{k!} n→∞limCnkpnk(1−pn)n−k=k!λke−λ
也就是说以n,p为参数的二项分布的概率值可以由参数为 λ = n p \lambda=np λ=np的泊松分布的概率值近似
3、随机变量的分布函数
定义:设X是一个随机变量,x是任意实数,函数
F(x)=P{X ≤ \leq ≤x},- ∞ \infty ∞
称为X的分布函数
对于任意实数 x 1 x_1 x1, x 2 x_2 x2( x 1 x_1 x1< x 2 x_2 x2),有
P{ x 1 x_1 x1
分布函数F(x)有以下的基本性质:
1、F(x)是一个不减函数
2、0 ≤ \leq ≤F(x) ≤ \leq ≤ 1,且
F ( − ∞ ) = lim x → − ∞ F ( x ) = 0 F(-\infty)=\lim\limits_{x\rightarrow -\infty}F(x)=0 F(−∞)=x→−∞limF(x)=0
F ( ∞ ) = lim x → ∞ F ( x ) = 1 F(\infty)=\lim\limits_{x\rightarrow \infty}F(x)=1 F(∞)=x→∞limF(x)=1
4、连续随机变量及其概率密度
如果对于随机变量X的分布函数F(x),存在非负函数f(x),使对于任意实数x有
F ( x ) = ∫ − ∞ x f ( t ) d t F(x)=\int_{-\infty}^{x} f(t)dt F(x)=∫−∞xf(t)dt
则称X为连续型随机变量,其中函数f(x)称为X的概率密度函数,简称概率密度
概率密度f(x)具有以下性质:
1、f(x) ≥ \geq ≥ 0
2、 ∫ − ∞ ∞ f ( x ) d x = 1 \int_{-\infty}^{\infty} f(x)dx=1 ∫−∞∞f(x)dx=1
3、对于任意实数 x 1 x_1 x1, x 2 x_2 x2( x 1 x_1 x1 ≤ \leq ≤ x 2 x_2 x2),
P{ x 1 x_1 x1
4、若f(x)在点x处连续,则有F ′ \prime ′(x)=f(x)
对于连续型随机变量X来说,它取任意指定实数值a的概率均为0,即P{X=a}=0
(一)均匀分布
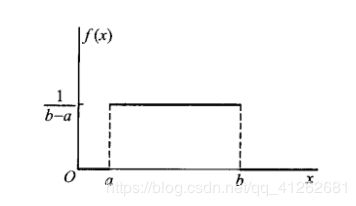
定义:若连续型随机变量X具有概率密度
f ( x ) = { 1 b − a , x ∈ ( a , b ) 0 , 其 他 f(x)=\begin{cases} {\frac{1}{b-a},x\in(a,b)}\\ {0,其他}\end{cases} f(x)={b−a1,x∈(a,b)0,其他
则称X在区间(a,b)上服从均匀分布,记为X~U(a,b)
易知f(x) ≥ \geq ≥ 0 ,且 ∫ − ∞ ∞ f ( x ) d x = 1 \int_{-\infty}^{\infty} f(x)dx=1 ∫−∞∞f(x)dx=1
性质:均匀分布具有等可能性
即对任一长度 l l l的子区间(c,c+ l l l),a ≤ \leq ≤c
P{c
即,服从U(a,b)上的均匀分布的随机变量X落入(a,b)中的任意子区间上的概率只与其区间长度有关,与区间位置无关
即,X落入(a,b)中的等长度的任意子区间上是等可能的
X的分布函数为
F(x)= { 0 , x < a x − a b − a , a ≤ x < b 1 , x ≥ b \begin{cases} {0,x<a}\\ {\frac{x-a}{b-a},a\leq x<b}\\{1,x\geq b}\end{cases} ⎩⎪⎨⎪⎧0,x<ab−ax−a,a≤x<b1,x≥b
(二)指数分布
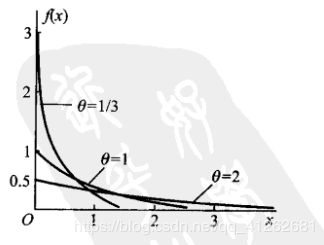
若连续型堆积变量X的概率密度为
f ( x ) = { 1 θ e − x / θ , x > 0 0 , 其 他 f(x)=\begin{cases} {\frac{1}{ \theta }e^{-x/\theta},x>0}\\ {0,其他}\end{cases} f(x)={θ1e−x/θ,x>00,其他
其中 θ \theta θ>0为常数,则称X服从参数为 θ \theta θ的指数分布,记为X~E( λ \lambda λ)
易知f(x) ≥ \geq ≥ 0 ,且 ∫ − ∞ ∞ f ( x ) d x = 1 \int_{-\infty}^{\infty} f(x)dx=1 ∫−∞∞f(x)dx=1
分布函数为
F(x)= { 1 − e − x / θ , x > 0 0 , 其 他 \begin{cases} {1-e^{-x/\theta},x>0}\\ {0,其他}\end{cases} {1−e−x/θ,x>00,其他
性质:指数分布具有无记忆性
对于s,t>0,有
P(X>s+t|X>s)=P{X>t}
(三)正态分布

性质:
1.f(x)关于x= μ \mu μ对称
2.当x ≤ \leq ≤ μ \mu μ时,f(x)是严格单调递增函数
3.f(max)=f( μ \mu μ)= 1 2 π σ \frac{1}{2\sqrt{\pi}\sigma} 2πσ1
4. lim ∣ x − μ ∣ → ∞ f ( x ) = 0 \lim\limits_{|x-\mu|\rightarrow \infty}f(x)=0 ∣x−μ∣→∞limf(x)=0
μ \mu μ为位置参数
σ \sigma σ为尺度参数, σ \sigma σ越小,图形越高越瘦, σ \sigma σ越大,图形越矮越胖

标准正态分布
当 μ \mu μ=0, σ \sigma σ=1时
概率密度用 φ \varphi φ(x)表示,分布函数用 ϕ \phi ϕ(x)表示