五一欢乐水题赛

大一的大佬们出的题，给我打自闭了。

A:熬夜的代价
题目大意：顺时针给n个点的坐标，保证所有点构成一个凸包，求取其中3~n个点时，曼哈顿距离的最大值。
思路：思路向曼哈顿距离的几何意义靠拢，画出图形你会发现，只要选取的点数大于等于4，那么只要选取max_x,max_y,min_x,min_y，就一定可以构造出和选取所有点时一样的最大矩形。所以只要判断取三个点的情况就好。
吐槽：当时看到距离的定义之后毫不在意，做图找思路的时候也是直接按照直线距离找，结果最后想的的从最后开始，倒着计算，每次去掉一条对总长度贡献最小的边，然后更新影响。错的离谱。对曼哈顿距离的几何意义不敏感，很尴尬。

#include 

using namespace std;
#define inf 0x3f3f3f3f
const int N=3e5+10;
int x[N],y[N];
int main()
{
    int n;cin>>n;
    int max_x=-inf,max_y=-inf;
    int min_x=inf,min_y=inf;
    for(int i=0;i<n;i++){
		cin>>x[i]>>y[i];
		max_x=max(max_x,x[i]);max_y=max(max_y,y[i]);
		min_x=min(min_x,x[i]);min_y=min(min_y,y[i]);
    }
    int res=0;
    for(int i=0;i<n;i++){
		res=max(res,2*abs(x[i]-max_x)+2*abs(y[i]-max_y) );
		res=max(res,2*abs(x[i]-max_x)+2*abs(y[i]-min_y) );
		res=max(res,2*abs(x[i]-min_x)+2*abs(y[i]-max_y) );
		res=max(res,2*abs(x[i]-min_x)+2*abs(y[i]-min_y) );
    }
    cout<<res;
	for(int i=n;i>=4;i--){
		cout<<" "<<2*(max_x-min_x)+2*(max_y-min_y);
    }
    cout<<endl;

    return 0;
}

B果光的评测姬
大意：模拟OJ判题，大模拟
思路：不会。
吐槽：题太长，不会写，交给队友，我，划水。

//果光的评测姬 By Guoguang
#include 
using namespace std;

char cases[11][5001]={0};
char thiscase[5001]={0};
int rc=0,cnum=0,sampleok=0,res,ucnum=0;
char line[1001],status={0};

void readtoEOC() //读取到测试点结束 
{
	while(gets(line))if(!strcmp(line,"END_OF_CASE"))break;
}

int readTestCase(char readBuf[]) //读取一个测试点到readBuf中 
{
	memset(readBuf,0,sizeof(readBuf));
	int ole=0;
	while(gets(line)!=NULL)
	{
		if(!strcmp(line,"END_OF_CASE")) //读取到测试点尾 
		{
			readBuf[strlen(readBuf)-1]=0; //结尾补\0 
			if(ole)return 0; //判断是否ole 
			else return 1;
		}
		if(!ole) //没有ole就继续读 
		{
			if(strlen(readBuf)+strlen(line)>5000) //ole了 
			{
				ole=1;
				continue;
			}
			line[strlen(line)+1]=0; //补\0 
			line[strlen(line)]='\n'; //加换行 
			strcat(readBuf,line); //读到的这行加到readBuf里 
		}
	}
}

int judge(char sampleop[],char userop[]) //评测 标准输出与用户输出 
{
	int lens=strlen(sampleop);
	int lenu=strlen(userop);
	if(!lenu)return 2; //没输出返回RE 
	if(!strcmp(sampleop,userop))return 0; //完全相同返回AC 
	if(lenu-lens==1&&userop[lenu-1]=='\n') //用户比标准输出多个换行 
	{
		userop[lenu-1]=0; //去掉多的换行进行比较 
		lenu--;
		if(!strcmp(sampleop,userop))return 0; //返回AC 
	}
	int sp=0,up=0;
	while(1)
	{
		while(up+1<lenu&&(userop[up]=='\n'||userop[up]==' '))up++; //忽略用户输出换行和回车 
		while(sp+1<lens&&(sampleop[sp]=='\n'||sampleop[sp]==' '))sp++; //忽略标准输出换行和回车 
		if(userop[up]!=sampleop[sp])return 4; //逐字符比较，不同返回WA 
		sp++;up++; //比较下一字符 
		
		if(up==lenu&&sp==lens)return 3; //同时结束返回PE 
		else if(up+1==lenu&&sp+1==lens) //只剩最后一个字符 
		{
			if((sampleop[sp]=='\n'||sampleop[sp]==' ')&&(userop[up]=='\n'||userop[up]==' ')||userop[up]==sampleop[sp])return 3;
			else return 4;
		}
		else if(up==lenu) //用户输出先结束 
		{
			while(sp+1<lens&&(sampleop[sp]=='\n'||sampleop[sp]==' '))sp++;
			if(sp+1==lens&&(sampleop[sp]=='\n'||sampleop[sp]==' '))return 3;
			else return 4;
		}
		else if(sp==lens) //标准输出先结束 
		{
			while(up+1<lenu&&(userop[up]=='\n'||userop[up]==' '))up++;
			if(up+1==lenu&&(userop[up]=='\n'||userop[up]==' '))return 3;
			else return 4;
		}
	}
}

void printans(int sta,char user[],int caseno) //输出答案 
{
	printf("USER %s\n",user);
	switch(sta)
	{
		case 0:
			printf("Accepted\n");
			break;
		case 1:
			printf("Output Limit Exceeded\n");
			break;
		case 2:
			printf("Runtime Error\n");
			break;
		case 3:
			printf("Presentation Error\n");
			break;
		case 4:
			printf("Wrong Answer at Case #%d\n",caseno);
			break;
		case 5:
			printf("Compile Error\n",caseno);
			break;
	}
	printf("\n");
}

int main()
{
	char cuser[21]={0};
	int csta,ccase,cskip;
	while(~scanf("%s",line)) //默认读取行的第一个单词 
	{
		if(!strcmp(line,"CASE_BEGIN")) //读取到测试点 
		{
			if(sampleok) //已读入标准输出（应读取用户输出） 
			{
				if(cskip) //已经停止对该用户的评测 （WA，RE，OLE时） 
				{
					readtoEOC(); //跳过该测试点 
					continue;
				}
				res=readTestCase(thiscase); //读测试点，返回值0为OLE 1为正常 
				if(!res)
				{
					printans(1,cuser,ccase); //输出OLE 
					cskip=1; //跳过该用户后续测试点 
					continue;
				}
				res=judge(cases[ccase++],thiscase); //评测，返回值与printans中的sta相对应 
				if(res==2||res==4)printans(res,cuser,ccase-1),cskip=1; //出错跳过并输出答案 
				if(csta!=3)csta=res; //非PE时记录该用户评测状态
			}
			else
			{
				readTestCase(cases[cnum++]); //读取到标准输出 
			}
		}
		if(!strcmp(line,"USER")) //读取到用户 
		{
			if(!cskip&&strlen(cuser)) //输出上一组用户结果 
			{
				printans(csta,cuser,0);
			}
			scanf("%s",cuser); //读用户名 
			sampleok=1; //已完成标准输出的读取 
			ccase=0; //当前测试点 
			csta=5; //默认CE（无测试点） 
			cskip=0; //不跳过该用户的评测 
			if(!strcmp(cuser,"guoguang")) //给自己开后门 
			{
				printans(0,cuser,0); //直接输出AC 
				cskip=1; //跳过评测阶段 
			}
		}
	}
	if(!cskip&&strlen(cuser)) //输出最后一组答案
	{
		printans(csta,cuser,0);
	}
	return 0;
}

Vae_1118的行列式
题目大意：给定一个无限大的行列式，观察行列式中的值，找出规律，然后给T个数字，依次给出T个数字在行列式中出现的次数，次数对p取模。
思路：行列式中的值=行数*列数+1，所以n的出现次数就是n-1的因子数。
吐槽：队友的神奇思路真的看不懂啊··，标程不是队友的那种真的太好了。

#include 

using namespace std;

int main()
{
    int T,mod; cin>>T>>mod;
    while(T--){
		int n;cin>>n;
		int i=1,res=0;
		n--;
		for(i=1;i*i<n;i++){
			if(n%i==0){
				res+=2;
			}
			if(res>mod) res%=mod;
		}
		if(i*i==n) res++;
		res%=mod;
		cout<<res<<endl;
    }
    return 0;
}

贴一份队友当时AC的代码，没看懂思路，但是水过去了，不知道是不是数据的问题，过两天问问队友本人怎么想的。

#include 
#include 
using namespace std;
int T,p,x;
int main()
{
    scanf("%d %d",&T,&p);
    while(T--)
    {
        scanf("%d",&x);
        int cnt=1;
        int add=1;
        int sum=0;
        int ans=0;
        while(1)
        {
            sum+=add;
            if(x>=sum+cnt)
            {
                if((x-sum)%cnt==0)
                {
                    if((x-sum)==cnt)
                    ans=(ans+1)%p;
                    else
                    ans=(ans+2)%p;
                }
                cnt++;
                if(cnt==2)
                add+=1;
                else
                add+=2;
            }
            else
            break;
        }
        printf("%d\n",ans);
    }
    return 0;
}

莫拉莱斯的矩阵难题
题目大意：给你一个矩阵，观察其描述方式，找出规律，然后给你一个初始数字Q，问第x层有多少个数字y。
思路：原矩阵规律，每一行都是对上一行的描述，比如第一行1，第二行1 1就可以理解为上一行是1个1，第三行2 1，就可以理解为上一行两个1，第四行1 2 1 1就是上一行一个2，一个1，依此类推。而题意要求的图又加了一条，行数从1开始，除第一行以外奇数行的描述都是每次尽可能少，比如上一行1 1 1 1 ，奇数行的描述就是 4 1; 而偶数行只能一个一个数字的描述，上一行是1 1 1 1，那偶数行就是 1 1 1 1 1 1 1 1。
找到规律之后开始打表，毕竟直接暴力肯定会T，算法必须是log的，能想到的就是数字出现个数有规律，题解的描述是，你会发现每次出现的数字肯定只有1，3，5，7和初始化的数字Q。
盗一份题解的图

然后是出现的次数

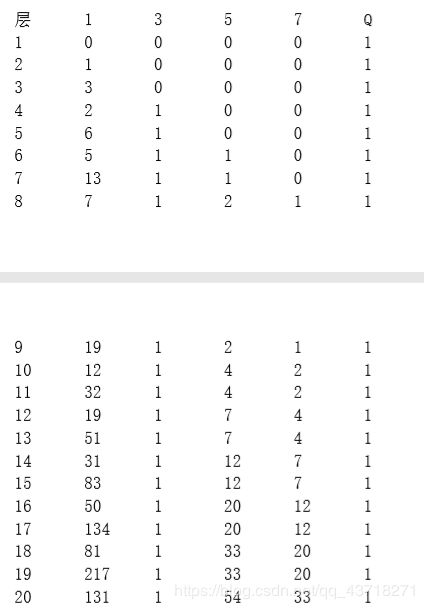
由于不询问1的出现次数，也就是维护5和7的出现次数，7的出现次数和5的规律相同，不过移位两个，相当于求5的出现规律即可。
题解的思路是出现次数f(x)=f(x-2)+f(x-4)+1，然后矩阵快速幂。我的思路是，每次出现的数字实际上都是斐波那契数列的前缀和，矩阵快速幂求斐波那契数列前缀和然后判断层数即可，但是没验证。
吐槽：这题思路太强了，届不到啊届不到，看表找规律太废柴了，这方面得多练练。

标程

/*
 * @ProblemId: 6
 * @Probtitle: Morales's MiG
 * @Location: GGOJ
 * @Author: Morales
 * @Date: 2020-04-30 13:57:01
 * @LastEditTime: 2020-04-30 19:24:31
 * @Space: https://space.bilibili.com/350869102
 * @E-mail: [email protected]
 * @Blog: https://blog.csdn.net/baidu_41248654
 * @Powered by: Havoc_Wei
 */
#include 
using namespace std;
const long long Mod = 20200501;
const long long pows[4][4] = {{0, 0, 0, 0}, {0, 1, 1, 0}, {0, 1, 0, 0}, {0, 1, 0, 1}};  //矩阵F
const long long start[4][4] = {{0, 0, 0, 0}, {0, 1, 0, 1}, {0, 0, 0, 0}, {0, 0, 0, 0}}; //矩阵A
const long long _01[4][4] = {{0, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}};   //矩阵的0次方
class node
{ //矩阵类
public:
    long long arr[4][4];
    node(void) { memset(arr, 0, sizeof(arr)); }
    node(const long long a[4][4])
    { //构造函数
        for (register int i = 1; i <= 3; ++i)
            for (register int j = 1; j <= 3; ++j)
                arr[i][j] = a[i][j];
    };
    friend node operator*(const node &x, const node &y)
    { //重载乘法运算
        node c;
        for (register int i = 1; i <= 3; ++i)
            for (register int j = 1; j <= 3; ++j)
                for (register int k = 1; k <= 3; ++k)
                    c.arr[i][j] += x.arr[i][k] * y.arr[k][j];
        return c;
    }
    node operator%(long long mod)
    { //重载模运算
        node c;
        for (register int i = 1; i <= 3; ++i)
            for (register int j = 1; j <= 3; ++j)
                c.arr[i][j] = arr[i][j] % mod;
        return c;
    }
} task(pows), st(start);
const node zero(_01);
node pow(node a, long long b, long long mod)
{ //精简的快速幂
    if (b == 0)
        return zero; //矩阵的0次方
    if (b == 1)
        return a;
    node t = pow(a, b >> 1, mod);
    if ((b & 1) == 1)
        return (((t * t) % mod) * a % mod);
    return t * t % mod;
}
int main(void)
{
    long long a, b, c;
    scanf("%lld%lld%lld", &a, &b, &c);
    b--;
    long long ans = (a == c);
    if (c == 3) //3那一列从3开始+1
        ans += (b > 2);
    if (c == 5)
    {
        if (b == 5)
            ans += 1;
        else if (b >= 6)
            ans += (st * pow(task, ((b - 5) >> 1), Mod)).arr[1][1];
        //不能写成 pow(task,((b-5)>>1),Mod)*st 因为矩阵乘法不满足交换律
    }
    if (c == 7)
    {
        if (b == 7)
            ans += 1;
        else if (b >= 8)
            ans += (st * pow(task, ((b - 7) >> 1), Mod)).arr[1][1];
    }
    printf("%lld", ans % Mod);
    return 0;
}

E是小学数学题吗？
题目大意: 给你一个矩阵A，然后矩阵B满足

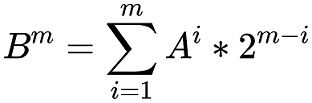
输出矩阵B的m次方的所有值，结果取模。

思路：矩阵快速幂，但是这题没有现成的关系可以找，也没有规律，唯一的方法就是构造，题解的构造思路是：

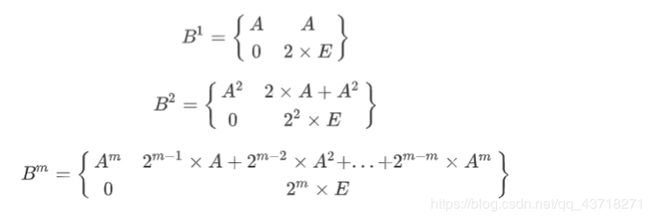
然后取右上角作为答案即可。
吐槽：矩阵快速幂，今年五一之前我就做了一个矩阵快速幂的题目，还是队友逼着补的。突然来个构造矩阵快速幂的，着实吓人，我自己板子放在哪个文件夹我都忘了····

标程

/*
 * @Author: NEFU_马家沟老三
 * @LastEditTime: 2020-04-28 22:40:05
 * @CSDN blog: https://blog.csdn.net/acm_durante
 * @E-mail: [email protected]
 * @ProbTitle:
 */
#include 
using namespace std;
typedef long long ll;
const double PI = acos(-1.0);
const ll mod = 1000000007;
int n;
struct Matrix
{
    ll m[70][70];
    Matrix() //初始化
    {
        memset(m, 0, sizeof(m));
    }
};
Matrix Multi(Matrix a, Matrix b) //矩阵乘法
{
    Matrix res;
    for (int i = 1; i <= 2 * n; i++)
        for (int j = 1; j <= 2 * n; j++)
            for (int k = 1; k <= 2 * n; k++)
                res.m[i][j] = (res.m[i][j] + a.m[i][k] * b.m[k][j]) % mod;
    return res;
}
Matrix fastm(Matrix a, int m) //矩阵快速幂
{
    Matrix res;
    for (int i = 1; i <= 2 * n; i++) //相当于普通快速幂中的res=1,注意
        res.m[i][i] = 1;
    while (m)
    {
        if (m & 1)
            res = Multi(res, a);
        a = Multi(a, a);
        m >>= 1;
    }
    return res;
}
int main()
{
    ios::sync_with_stdio(false);
    int m;
    Matrix num;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) //构造矩阵B
        for (int j = 1; j <= n; j++)
        {
            cin >> num.m[i][j];
            num.m[i][j + n] = num.m[i][j];
        }
    for (int i = n + 1; i <= 2 * n; i++) //构造矩阵B
        num.m[i][i] = 2;
    Matrix ans = fastm(num, m);  //矩阵快速幂
    for (int i = 1; i <= n; i++) //输出答案矩阵
        for (int j = n + 1; j <= 2 * n; j++)
        {
            cout << ans.m[i][j];
            if (j != 2 * n)
                cout << " ";
            else
                cout << endl;
        }
    return 0;
}

F我要去看流星雨
题目大意：给n个三维坐标点，保证坐标均为整数，每一个点有一个亮度，如果两个点相邻(距离为1)且亮度差不超过m，则划分为一个区域，问最后划分成多少个区域及最大的区域有多少星星。
思路：并查集。
吐槽：队友说看一眼就知道是并查集裸题，然后我，嗯，不会。
代码

#include 
using namespace std;
const int N=1e4+10;
int n,m,p[N],si[N];
struct node
{
    int x,y,z,w;
}a[N];
int find(int x)
{
	if(p[x] != x) p[x] = find(p[x]);
	return p[x];
}

void join(int x,int y)
{
	p[find(x)] = p[y];
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i].x>>a[i].y>>a[i].z>>a[i].w;
        p[i]=i;
        si[i]=1;//i点所在连通块大小
    }
    int cnt=0;//连通块个数
    for(int i=1;i<=n;i++)
    {
        int x=a[i].x;
        int y=a[i].y;
        int z=a[i].z;
        int w=a[i].w;
        for(int j=i+1;j<=n;j++)
        {
            int x2=a[j].x;
            int y2=a[j].y;
            int z2=a[j].z;
            int w2=a[j].w;
            if(abs(x2-x)+abs(y2-y)+abs(z2-z)<=1&&abs(w2-w)<=m)
            {
                if(find(i)!=find(j))//不在同一连通块
                {
                    si[p[j]]+=si[p[i]];
                    join(i,j);
                }
            }
        }
    }
    int mx=-1;
    for(int i=1;i<=n;i++)
    {
        if(p[i]==i)cnt++;
        //printf("%d\n",si[p[i]]);
        mx=max(mx,si[p[i]]);

    }
    printf("%d %d\n",cnt,mx);
    return 0;
}

G人类的本质是什么？
题目大意：给n个时间，每一个时间表示一个人复读需要的时间，每个人都复读一次，至少需要多长时间，当第一个复读超过1/4之后，第二个人就可以开始复读。
思路：贪心模拟，把每个人复读的时间从大到小排序，然后维护每个人复读结束的时间。
吐槽：这个题意，刚开始和队友争论到底是什么意思，很佛，八个字取两个字，所以按1/4算，我这么想了，没敢写，没想到真的是，很佛。
代码

#include 
#include 
#include 
using namespace std;
const int maxn=1e4+5;
double a[maxn];
int n;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    scanf("%lf",&a[i]);
    sort(a+1,a+1+n,greater<double>());
    double sum=0.0;
    sum+=a[1];
    double sub=a[1]/4.0;
    double last=a[1]-sub;
    for(int i=2;i<=n;i++)
    if(a[i]<=last)
    {
        sub=a[i]/4.0;
        last-=sub;
    }
    else
    {
        sub=a[i]/4.0;
        sum+=a[i]-last;
        last=a[i]-sub;
    }
    printf("%.2lf\n",sum);
    return 0;
}

H卡迪亚的游戏
题目大意：游戏总数n，每个游戏有占用大小还有喜爱程度，求在内存m已知的情况下放入游戏能获得的最大喜爱程度。
思路：背包，因为占用大小范围1~1e9，所以背包第二维改成喜爱程度，dp值存储占用大小。然后跑一遍所以喜爱程度，如果dp值小于等于m，更新ans。
吐槽：背包也好几个月没碰了，WA了12次还是多少次，最后二维背包改成一维就过了，赛后发现自己二维背包的dp方程，dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]), 写成dp[i][j]=max(dp[i][j],dp[i][j-w[i]]+v[i])了，关键是我自己写的例子还都过了，我改了半天的初始值。
代码

#include 
#include 
using namespace std;
typedef long long LL;
const LL inf=1e14;
LL a[100*100+5];
LL w[105],v[105];
int main()
{

	int n,m,limit=0; cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>v[i]>>w[i];
		limit+=w[i];
	}

		for(int j=0;j<=10000+1;j++)
			a[j]=inf;

	a[0]=0;

	for(int i=1;i<=n;i++){
		for(int j=limit;j>=0;j--){
			if(j>=w[i]){
				a[j]=min(a[j],a[j-w[i]]+v[i]);
			}
		}
	}

//

//		for(int j=0;j<=limit;j++){
//			cout<
//		}
//		cout<


	LL res=0;

		for(LL j=1;j<=limit;j++){
			if(a[j]<=m){
				res=max(res,j);
			}
		}

	cout<<res<<endl;
    return 0;
}

I老爷机
题目大意：给你总时间 t 和n个游戏，碰到游戏时必须开始玩游戏，问空闲时间的最大值和最小值。
思路：线段覆盖的dp题目，从后往前开始维护dp值，比较好理解的dp方程是，
if(此时没有游戏开始) dp[i]=dp[i+1]+1
else dp[i]=min(dp[i],dp[从当前时间开始的游戏右端点])
因为这个dp方程当前状态和之后状态有关，所以从后往前写比较方便，我记得有从前往后的方法，不知道是不是没记清楚。这个题目因为问了两个值，所以用两个dp数组，一个维护最大值，一个维护最小值即可。
吐槽：这题当然见过，比赛的时候没敢做啊，怎么可能就是个简单的dp维护呢，过的人那么少，然后神仙队友线段树维护结果，大佬NP，然后MLE，TLE，逐渐自闭。
代码(标程代码，改了点细节做实验)

/*
 * @Author: Gehrychiang
 * @LastEditTime: 2020-04-24 22:03:44
 * @Website: www.yilantingfeng.site
 * @E-mail: [email protected]
 * @ProbTitle: 老爷机
 */
//#pragma GCC optimize(2)
//线性dp，最后整合答案输出即可
#include 
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;

struct node
{
    int l;
    int r;
};
node in[100005];
int cnt[100005];
int dp1[100005]; //老爷机最多休息
int dp2[100005]; //老爷机最少休息
bool comp(node m, node n)
{
    if (m.l != n.l)
    {
        return m.l < n.l;
    }
    else
    {
        return m.r < n.r;
    }
}
int main()
{
    memset(dp1, 0, sizeof(dp1));
    memset(dp2, inf, sizeof(dp2));
    int t, n;
    cin >> t >> n;
	dp2[t+1]=0;
    for (int i = 0; i < n; i++)
    {
        cin >> in[i].l >> in[i].r;
        cnt[in[i].l]++; //记录开始时间
    }
    sort(in, in + n, comp);
     int p = n-1;
    for (int i = t; i >= 1; i--)
    {
        if (cnt[i] == 0) //空闲
        {
            dp1[i] = dp1[i + 1] + 1;
            dp2[i] = dp2[i + 1] + 1;
        }
        else
        {
            for (int j = 0; j < cnt[i]; j++)
            {
                dp1[i] = max(dp1[i], dp1[in[p].r]);
                dp2[i] = min(dp2[i], dp2[in[p--].r]);
            }
        }
    }
    //cout<<"最长休息时间: "<
     cout << 4 * dp2[1] + 3 * dp1[1] << endl;
    return 0;
}

补充
题目说白了就是线段覆盖问题，关于贪心解和dp解的区别，一般在与结果是否和线段的长度有关。
贪心解的常见题型如
1.给n个区间，去掉最少的区间，保证剩下的区间两两不相交。
考虑区间相交的时候，有两个区间有交集，我们肯定留下右端点比较小的那个，这样就能对剩下的区间的影响最小，保证最后留下的区间尽可能多，所以按照区间右端点排序即可。
2.给n个区间，用最少的区间保证完全覆盖一个给定的区间。
首先我们必须明确，当这个区间和给定的区间完全没有交集的时候我们肯定要把这个区间舍弃，那么我们要做的就是在剩下的，和给定区间肯定有交集的区间中选择。
当我们把其中一个区间去掉的时候，设左右端点分别是[x,y], [x,y]必然是已经被我们选择的其他区间所覆盖，即x>=已经覆盖的部分的左端点，y<=已经覆盖的部分的右端点。
所以我们只需要按照左端点进行排序，每加入一个新的区间，就更新已经覆盖的部分的右端点，如果这个新的区间已经被覆盖，那就去掉它。
值得注意的是，贪心解全都是解决个数问题，而dp解法全都是解决如上面的I题所示的长度问题。

J提莫队长正在待命
题目大意：给你一个图，分陆地，城堡，水，森林。你可以在森林里种直径为5的十字炸弹，保证炸弹范围不重叠且不会伤害到城堡，问最多可以种多少个炸弹。
思路：正常的话dfs暴力，但是时间不够，空间不够，状压dp优化，因为当前行状态和前两行的状态相关，所以三个维度dp[行数][上一行状态][上上行状态], 因为每一行m<=10, 总情况1024可以接受，行数开滚动数组mod2优化即可。
吐槽：思路看起来很清晰，但是细节好多，所以不会写(菜的理直气壮)。

/*
 * @Author: Gehrychiang
 * @LastEditTime: 2020-05-03 19:26:04
 * @Website: www.yilantingfeng.site
 * @E-mail: [email protected]
 * @ProbTitle: 提莫队长正在待命
 */
#pragma GCC optimize(2)
#include 
using namespace std;
typedef long long ll;
char district[105][15];//存图
int dp[5][1100][1100]; //到第i行，第i行状态为j，上一行状态为k,同时考虑每一行只与上两行有关所以滚动数组优化
bool chksg[105][1100];
bool chkdual[1100][1100];
int n, m, maxm, ans = 0;
bool chka(int line, int sit) //检查当前行状态是否合法
{
    //不可以放在除森林以外的任何地方并且需要满足彼此间隔大于等于3
    int las = -1;
    for (int i = 0; i < m; i++)
    {
        if (((sit >> i) & 1) == 1)
        {
            if (las == -1) //直接更新
            {
                las = i;
            }
            else
            {
                if (i - las < 3)
                {
                    return false;
                }
                else
                {
                    las = i;
                }
            }
            if (district[line][m - i] != 'F')
            {
                return false;
            }
        }
    }
    return true;
}
bool chkb(int down, int up) //检查两行蘑菇之间是否会冲突
{
    int nt = (up & down);
    return nt == 0;
}
void init() //预处理情况
{
    for (int i = 1; i <= n; i++)
    {
        for (int j = 0; j <= maxm; j++)
        {
            chksg[i][j] = chka(i, j);
        }
    }
    for (int i = 0; i <= maxm; i++)
    {
        for (int j = 0; j <= maxm; j++)
        {
            chkdual[i][j] = chkb(i, j);
        }
    }
}
int main()
{
    //freopen("","r",stdin);
    //freopen("","w",stdout);
    cin >> n >> m;
    maxm = ((1 << m) - 1);
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> district[i][j];
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            if (district[i][j] == 'F')
            {
                for (int p = -2; p <= 2; p++) //考虑将城池的范围直接更改为不可放置即可
                {
                    if (i + p >= 1 && i + p <= n && district[i + p][j] == 'C')
                    {
                        district[i][j] = 'L';
                    }
                    if (j + p >= 1 && j + p <= m && district[i][j + p] == 'C')
                    {
                        district[i][j] = 'L';
                    }
                }
            }
        }
    }
    //预处理chk的情况
    init();
    //考虑第一行只要合法就直接放
    for (int i = 0; i <= maxm; i++)
    {
        if (chksg[1][i])
        {
            dp[1 % 2][i][0] = __builtin_popcount(i);
            ans = max(ans, dp[1 % 2][i][0]);
        }
    }
    //考虑第二行只要不与第一行冲突就可以直接放
    for (int i = 0; i <= maxm; i++)
    {
        if (chksg[2][i])
        {
            for (int j = 0; j <= maxm; j++)
            {
                if (chksg[1][j] && chkdual[i][j])
                {
                    dp[2 % 2][i][j] = dp[1 % 2][j][0] + __builtin_popcount(i);
                    ans = max(ans, dp[2 % 2][i][j]);
                }
            }
        }
    }
    //之后情况
    for (int i = 3; i <= n; i++)
    {
        for (int j = 0; j <= maxm; j++) //枚举当前行情况
        {
            if (chksg[i][j]) //检查当前行是否合法
            {
                int cnt = (int)__builtin_popcount(j);
                for (int k = 0; k <= maxm; k++) //枚举上一行情况
                {
                    if (chksg[i - 1][k] && chkdual[j][k]) //检查上一行状态是否合法并且是否会与当前行冲突
                    {
                        for (int p = 0; p <= maxm; p++) //枚举上上一行情况
                        {
                            if (chkdual[j][p]) //检查上上一行与当前行是否冲突
                            {
                                dp[i % 2][j][k] = max(dp[i % 2][j][k], dp[(i - 1) % 2][k][p] + cnt);
                                if (i == n)
                                {
                                    ans = max(ans, dp[i % 2][j][k]);
                                }
                            }
                        }
                    }
                }
            }
        }
    }
    cout << ans << endl;
    return 0;
}