笔记:动手学深度学习pytorch(批量归一化和残差网络,凸优化,梯度下降)
- 批量归一化和残差网络
- 批量归一化
- 对输入的标准化(浅层模型)
处理后的任意一个特征在数据集中所有样本上的均值为0、标准差为1。
标准化处理输入数据使各个特征的分布相近
- 批量归一化(深度模型)
利用小批量上的均值和标准差,不断调整神经网络中间输出,从而使整个神经网络在各层的中间输出的数值更稳定。
- 对全连接层做批量归一化
位置:全连接层中的仿射变换和激活函数之间
- 全连接
全连接层的数学模型:
x = W u + b \boldsymbol{x = Wu + b} x=Wu+b
o u t p u t = ϕ ( x ) \boldsymbol{output = \phi(x)} output=ϕ(x)
- 批量归一化
o u t p u t = ϕ ( W u + b ) \boldsymbol{output=\phi(Wu+b)} output=ϕ(Wu+b)
y ( i ) = BN ( x ( i ) ) \boldsymbol{y}^{(i)} = \text{BN}(\boldsymbol{x}^{(i)}) y(i)=BN(x(i))
μ B ← 1 m ∑ i = 1 m x ( i ) \boldsymbol{\mu}_\mathcal{B} \leftarrow \frac{1}{m}\sum_{i = 1}^{m} \boldsymbol{x}^{(i)} μB←m1∑i=1mx(i)
σ B 2 ← 1 m ∑ i = 1 m ( x ( i ) − μ B ) 2 \boldsymbol{\sigma}_\mathcal{B}^2 \leftarrow \frac{1}{m} \sum_{i=1}^{m}(\boldsymbol{x}^{(i)} - \boldsymbol{\mu}_\mathcal{B})^2 σB2←m1∑i=1m(x(i)−μB)2
x ^ ( i ) ← x ( i ) − μ B σ B 2 + ϵ , \hat{\boldsymbol{x}}^{(i)} \leftarrow \frac{\boldsymbol{x}^{(i)} - \boldsymbol{\mu}_\mathcal{B}}{\sqrt{\boldsymbol{\sigma}_\mathcal{B}^2 + \epsilon}}, x^(i)←σB2+ϵx(i)−μB,
其中 ϵ > 0 \epsilon>0 ϵ>0,且 ϵ \epsilon ϵ是一个很小的常数,这样能保证上式分母大于0
以此推出:
y ( i ) ← γ ⊙ x ^ ( i ) + β . {\boldsymbol{y}}^{(i)} \leftarrow \boldsymbol{\gamma} \odot \hat{\boldsymbol{x}}^{(i)} + \boldsymbol{\beta}. y(i)←γ⊙x^(i)+β.
引入可学习参数:拉伸参数 γ \gamma γ和偏移参数 β \beta β。若 γ = σ B 2 + ϵ \boldsymbol{\gamma = {\sqrt{{\sigma}_\mathcal{B}^2+\epsilon}}} γ=σB2+ϵ和 β = μ B \boldsymbol{\beta=\mu_B} β=μB,批量归一化无效。
- 对卷积层做批量归一化
位置:卷积计算之后、应⽤激活函数之前。
如果卷积计算输出多个通道,我们需要对这些通道的输出分别做批量归一化,且每个通道都拥有独立的拉伸和偏移参数。 计算:对单通道,batchsize=m,卷积计算输出=pxq 对该通道中m×p×q个元素同时做批量归一化,使用相同的均值和方差。
- 预测时的批量归一化
训练:以batch为单位,对每个batch计算均值和方差。
预测:用移动平均估算整个训练数据集的样本均值和方差。
def batch_norm(is_training, X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 判断当前模式是训练模式还是预测模式
if not is_training:
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean) ** 2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。这里我们需要保持
# X的形状以便后面可以做广播运算
mean = X.mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
var = ((X - mean) ** 2).mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
# 训练模式下用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 拉伸和偏移
return Y, moving_mean, moving_var
class BatchNorm(nn.Module):
def __init__(self, num_features, num_dims):
super(BatchNorm, self).__init__()
if num_dims == 2:
shape = (1, num_features) #全连接层输出神经元
else:
shape = (1, num_features, 1, 1) #通道数
# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成0和1
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
# 不参与求梯度和迭代的变量,全在内存上初始化成0
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.zeros(shape)
def forward(self, X):
# 如果X不在内存上,将moving_mean和moving_var复制到X所在显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的moving_mean和moving_var, Module实例的traning属性默认为true, 调用.eval()后设成false
Y, self.moving_mean, self.moving_var = batch_norm(self.training,
X, self.gamma, self.beta, self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.9)
return Y
再LeNet上的应用是这样的
net = nn.Sequential(
nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
BatchNorm(6, num_dims=4),
nn.Sigmoid(),
nn.MaxPool2d(2, 2), # kernel_size, stride
nn.Conv2d(6, 16, 5),
BatchNorm(16, num_dims=4),
nn.Sigmoid(),
nn.MaxPool2d(2, 2),
d2l.FlattenLayer(),
nn.Linear(16*4*4, 120),
BatchNorm(120, num_dims=2),
nn.Sigmoid(),
nn.Linear(120, 84),
BatchNorm(84, num_dims=2),
nn.Sigmoid(),
nn.Linear(84, 10)
)
print(net)
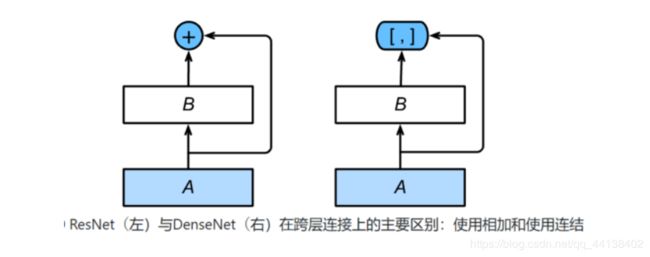
- 残差网络(ResNet)
深度学习的问题:深度CNN网络达到一定深度后再一味地增加层数并不能带来进一步地分类性能提高,反而会招致网络收敛变得更慢,准确率也变得更差。
- 残差块
- ResNet
- 稠密连接网络(DenseNet)
- 主要构建模块
稠密块(dense block): 定义了输入和输出是如何连结的。
过渡层(transition layer):用来控制通道数,使之不过大。
- 稠密块
def conv_block(in_channels, out_channels):
blk = nn.Sequential(nn.BatchNorm2d(in_channels),
nn.ReLU(),
nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
return blk
class DenseBlock(nn.Module):
def __init__(self, num_convs, in_channels, out_channels):
super(DenseBlock, self).__init__()
net = []
for i in range(num_convs):
in_c = in_channels + i * out_channels
net.append(conv_block(in_c, out_channels))
self.net = nn.ModuleList(net)
self.out_channels = in_channels + num_convs * out_channels # 计算输出通道数
def forward(self, X):
for blk in self.net:
Y = blk(X)
X = torch.cat((X, Y), dim=1) # 在通道维上将输入和输出连结
return X
- 过渡层
1 × 1 1 \times 1 1×1卷积层:来减小通道数
步幅为2的平均池化层:减半高和宽
def transition_block(in_channels, out_channels):
blk = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.ReLU(),
nn.Conv2d(in_channels, out_channels, kernel_size=1),
nn.AvgPool2d(kernel_size=2, stride=2))
return blk
blk = transition_block(23, 10)
blk(Y).shape # torch.Size([4, 10, 4, 4])
- DenseNet模型
net = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
num_channels, growth_rate = 64, 32 # num_channels为当前的通道数
num_convs_in_dense_blocks = [4, 4, 4, 4]
for i, num_convs in enumerate(num_convs_in_dense_blocks):
DB = DenseBlock(num_convs, num_channels, growth_rate)
net.add_module("DenseBlosk_%d" % i, DB)
# 上一个稠密块的输出通道数
num_channels = DB.out_channels
# 在稠密块之间加入通道数减半的过渡层
if i != len(num_convs_in_dense_blocks) - 1:
net.add_module("transition_block_%d" % i, transition_block(num_channels, num_channels // 2))
num_channels = num_channels // 2
net.add_module("BN", nn.BatchNorm2d(num_channels))
net.add_module("relu", nn.ReLU())
net.add_module("global_avg_pool", d2l.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, num_channels, 1, 1)
net.add_module("fc", nn.Sequential(d2l.FlattenLayer(), nn.Linear(num_channels, 10)))
X = torch.rand((1, 1, 96, 96))
for name, layer in net.named_children():
X = layer(X)
print(name, ' output shape:\t', X.shape)
#batch_size = 256
batch_size=16
# 如出现“out of memory”的报错信息,可减小batch_size或resize
train_iter, test_iter =load_data_fashion_mnist(batch_size, resize=96)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
- 凸优化
- 优化与深度学习
- 优化与估计
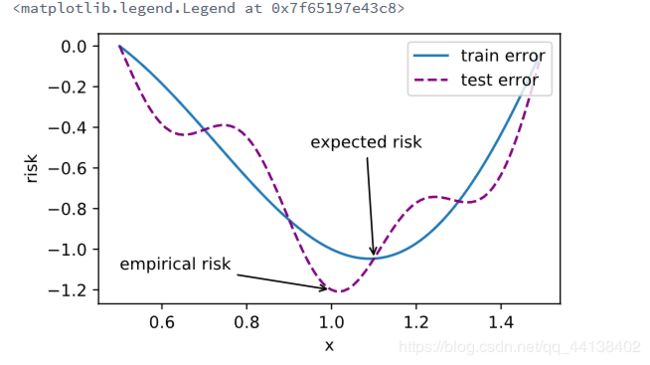
尽管优化方法可以最小化深度学习中的损失函数值,但本质上优化方法达到的目标与深度学习的目标并不相同。
- 优化方法目标:训练集损失函数值
- 深度学习目标:测试集损失函数值(泛化性)
def f(x): return x * np.cos(np.pi * x)
def g(x): return f(x) + 0.2 * np.cos(5 * np.pi * x)
d2l.set_figsize((5, 3))
x = np.arange(0.5, 1.5, 0.01)
fig_f, = d2l.plt.plot(x, f(x),label="train error")
fig_g, = d2l.plt.plot(x, g(x),'--', c='purple', label="test error")
fig_f.axes.annotate('empirical risk', (1.0, -1.2), (0.5, -1.1),arrowprops=dict(arrowstyle='->'))
fig_g.axes.annotate('expected risk', (1.1, -1.05), (0.95, -0.5),arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('risk')
d2l.plt.legend(loc="upper right")
- 优化在深度学习中的挑战
- 局部最小值
- 鞍点
- 梯度消失
例如:
f ( x ) = x cos π x f(x) = x\cos \pi x f(x)=xcosπx
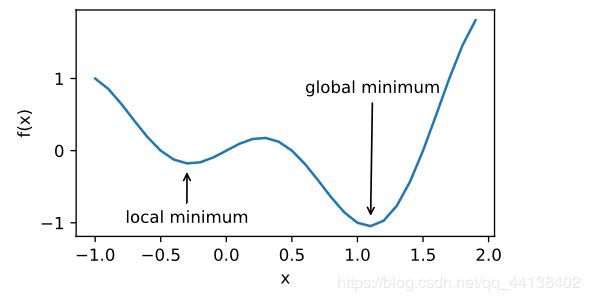
- 局部最小值
def f(x):
return x * np.cos(np.pi * x)
d2l.set_figsize((4.5, 2.5))
x = np.arange(-1.0, 2.0, 0.1)
fig, = d2l.plt.plot(x, f(x))
fig.axes.annotate('local minimum', xy=(-0.3, -0.25), xytext=(-0.77, -1.0),
arrowprops=dict(arrowstyle='->'))
fig.axes.annotate('global minimum', xy=(1.1, -0.95), xytext=(0.6, 0.8),
arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)');
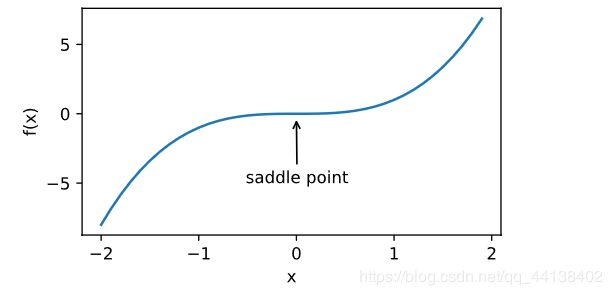
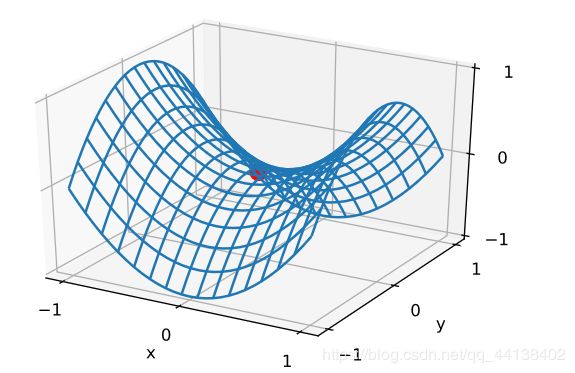
- 鞍点
x = np.arange(-2.0, 2.0, 0.1)
fig, = d2l.plt.plot(x, x**3)
fig.axes.annotate('saddle point', xy=(0, -0.2), xytext=(-0.52, -5.0),
arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)');
x, y = np.mgrid[-1: 1: 31j, -1: 1: 31j]
z = x**2 - y**2
d2l.set_figsize((6, 4))
ax = d2l.plt.figure().add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z, **{'rstride': 2, 'cstride': 2})
ax.plot([0], [0], [0], 'ro', markersize=10)
ticks = [-1, 0, 1]
d2l.plt.xticks(ticks)
d2l.plt.yticks(ticks)
ax.set_zticks(ticks)
d2l.plt.xlabel('x')
d2l.plt.ylabel('y');
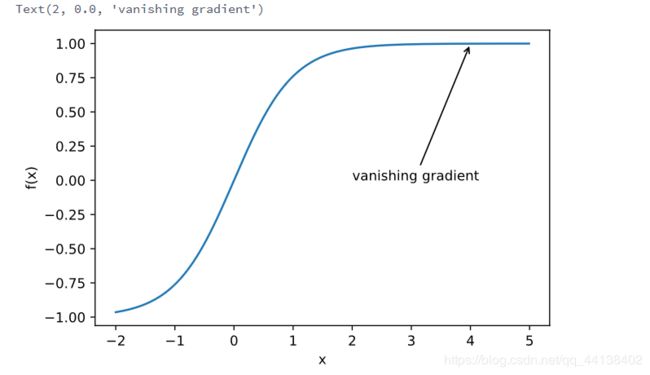
- 梯度消失
x = np.arange(-2.0, 5.0, 0.01)
fig, = d2l.plt.plot(x, np.tanh(x))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)')
fig.axes.annotate('vanishing gradient', (4, 1), (2, 0.0) ,arrowprops=dict(arrowstyle='->'))0
- 凸性(Convexity)
- 基础
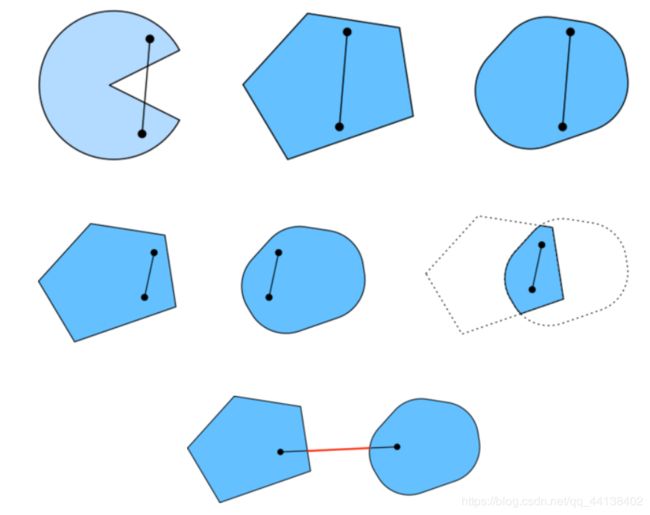
- 集合
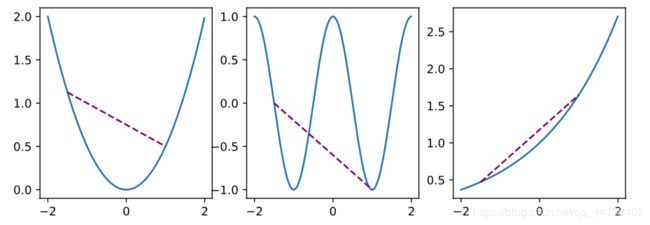
- 函数
λ f ( x ) + ( 1 − λ ) f ( x ′ ) ≥ f ( λ x + ( 1 − λ ) x ′ ) \lambda f(x)+(1-\lambda) f\left(x^{\prime}\right) \geq f\left(\lambda x+(1-\lambda) x^{\prime}\right) λf(x)+(1−λ)f(x′)≥f(λx+(1−λ)x′)
def f(x):
return 0.5 * x**2 # Convex
def g(x):
return np.cos(np.pi * x) # Nonconvex
def h(x):
return np.exp(0.5 * x) # Convex
x, segment = np.arange(-2, 2, 0.01), np.array([-1.5, 1])
d2l.use_svg_display()
_, axes = d2l.plt.subplots(1, 3, figsize=(9, 3))
for ax, func in zip(axes, [f, g, h]):
ax.plot(x, func(x))
ax.plot(segment, func(segment),'--', color="purple")
# d2l.plt.plot([x, segment], [func(x), func(segment)], axes=ax)
- Jense不等式
∑ i α i f ( x i ) ≥ f ( ∑ i α i x i ) and E x [ f ( x ) ] ≥ f ( E x [ x ] ) \sum_{i} \alpha_{i} f\left(x_{i}\right) \geq f\left(\sum_{i} \alpha_{i} x_{i}\right) \text { and } E_{x}[f(x)] \geq f\left(E_{x}[x]\right) ∑iαif(xi)≥f(∑iαixi) and Ex[f(x)]≥f(Ex[x])
- 性质
- 无局部极小值
- 与凸集的关系
- 二阶条件
- 无局部最小值
证明:假设存在 x ∈ X x \in X x∈X是局部最小值,则存在全局最小值 x ′ ∈ X x' \in X x′∈X, 使得 f ( x ) > f ( x ′ ) f(x)>f(x') f(x)>f(x′), 则对 λ ∈ ( 0 , 1 ] \lambda \in(0,1] λ∈(0,1]:
f ( x ) > λ f ( x ) + ( 1 − λ ) f ( x ′ ) ≥ f ( λ x + ( 1 − λ ) x ′ ) f(x)>\lambda f(x)+(1-\lambda) f(x^{\prime}) \geq f(\lambda x+(1-\lambda) x^{\prime}) f(x)>λf(x)+(1−λ)f(x′)≥f(λx+(1−λ)x′)
- 与凸集的关系
对于凸函数 f ( x ) f(x) f(x),定义集合 S b : = { x ∣ x ∈ X and f ( x ) ≤ b } S_{b}:=\{x | x \in X \text { and } f(x) \leq b\} Sb:={x∣x∈X and f(x)≤b},则集合 S b S_b Sb为凸集。
证明:对于点 x x x, x ′ ∈ S b x' \in S_{b} x′∈Sb有 f ( λ x + ( 1 − λ ) x ′ ) ≤ λ f ( x ) + ( 1 − λ ) f ( x ′ ) ≤ b f\left(\lambda x+(1-\lambda) x^{\prime}\right) \leq \lambda f(x)+(1-\lambda) f\left(x^{\prime}\right) \leq b f(λx+(1−λ)x′)≤λf(x)+(1−λ)f(x′)≤b,故 λ x + ( 1 − λ ) x ′ ∈ S b \lambda x+(1-\lambda) x^{\prime} \in S_{b} λx+(1−λ)x′∈Sb
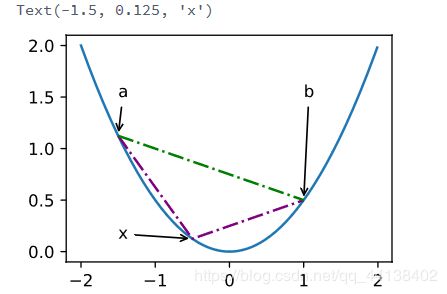
对于函数 f ( x , y ) = 0.5 x 2 + c o s ( 2 π y ) f(x,y)=0.5x^2+cos(2 \pi y) f(x,y)=0.5x2+cos(2πy)
def f(x):
return 0.5 * x**2
x = np.arange(-2, 2, 0.01)
axb, ab = np.array([-1.5, -0.5, 1]), np.array([-1.5, 1])
d2l.set_figsize((3.5, 2.5))
fig_x, = d2l.plt.plot(x, f(x))
fig_axb, = d2l.plt.plot(axb, f(axb), '-.',color="purple")
fig_ab, = d2l.plt.plot(ab, f(ab),'g-.')
fig_x.axes.annotate('a', (-1.5, f(-1.5)), (-1.5, 1.5),arrowprops=dict(arrowstyle='->'))
fig_x.axes.annotate('b', (1, f(1)), (1, 1.5),arrowprops=dict(arrowstyle='->'))
fig_x.axes.annotate('x', (-0.5, f(-0.5)), (-1.5, f(-0.5)),arrowprops=dict(arrowstyle='->'))
- 凸函数与二阶导数
f ′ ′ ( x ) ≥ 0 ⟺ f ( x ) f^{''}(x) \ge 0 \Longleftrightarrow f(x) f′′(x)≥0⟺f(x)是凸函数
必要性( ⇐ \Leftarrow ⇐):
对于凸函数:
1 2 f ( x + ϵ ) + 1 2 f ( x − ϵ ) ≥ f ( x + ϵ 2 + x − ϵ 2 ) = f ( x ) \frac{1}{2} f(x+\epsilon)+\frac{1}{2} f(x-\epsilon) \geq f\left(\frac{x+\epsilon}{2}+\frac{x-\epsilon}{2}\right)=f(x) 21f(x+ϵ)+21f(x−ϵ)≥f(2x+ϵ+2x−ϵ)=f(x)
可以得到:
f ′ ′ ( x ) = lim ε → 0 f ( x + ϵ ) − f ( x ) ϵ − f ( x ) − f ( x − ϵ ) ϵ ϵ f^{\prime \prime}(x)=\lim _{\varepsilon \rightarrow 0} \frac{\frac{f(x+\epsilon) - f(x)}{\epsilon}-\frac{f(x) - f(x-\epsilon)}{\epsilon}}{\epsilon} f′′(x)=limε→0ϵϵf(x+ϵ)−f(x)−ϵf(x)−f(x−ϵ)
f ′ ′ ( x ) = lim ε → 0 f ( x + ϵ ) + f ( x − ϵ ) − 2 f ( x ) ϵ 2 ≥ 0 f^{\prime \prime}(x)=\lim _{\varepsilon \rightarrow 0} \frac{f(x+\epsilon)+f(x-\epsilon)-2 f(x)}{\epsilon^{2}} \geq 0 f′′(x)=limε→0ϵ2f(x+ϵ)+f(x−ϵ)−2f(x)≥0
充分性( ⇒ \Rightarrow ⇒):
令 a < x < b a
f ( x ) − f ( a ) = ( x − a ) f ′ ( α ) for some α ∈ [ a , x ] and f ( b ) − f ( x ) = ( b − x ) f ′ ( β ) for some β ∈ [ x , b ] \begin{array}{l}{f(x)-f(a)=(x-a) f^{\prime}(\alpha) \text { for some } \alpha \in[a, x] \text { and }} \\ {f(b)-f(x)=(b-x) f^{\prime}(\beta) \text { for some } \beta \in[x, b]}\end{array} f(x)−f(a)=(x−a)f′(α) for some α∈[a,x] and f(b)−f(x)=(b−x)f′(β) for some β∈[x,b]
根据函数单调性原理:
f ′ ( β ) ≥ f ′ ( α ) f^{\prime}(\beta) \geq f^{\prime}(\alpha) f′(β)≥f′(α)
所以可以得到:
f ( b ) − f ( a ) = f ( b ) − f ( x ) + f ( x ) − f ( a ) = ( b − x ) f ′ ( β ) + ( x − a ) f ′ ( α ) ≥ ( b − a ) f ′ ( α ) \begin{aligned} f(b)-f(a) &=f(b)-f(x)+f(x)-f(a) \\ &=(b-x) f^{\prime}(\beta)+(x-a) f^{\prime}(\alpha) \\ & \geq(b-a) f^{\prime}(\alpha) \end{aligned} f(b)−f(a)=f(b)−f(x)+f(x)−f(a)=(b−x)f′(β)+(x−a)f′(α)≥(b−a)f′(α)
- 限制条件
minimize x f ( x ) subject to c i ( x ) ≤ 0 for all i ∈ { 1 , … , N } \begin{array}{l}{\underset{\mathbf{x}}{\operatorname{minimize}} f(\mathbf{x})} \\ {\text { subject to } c_{i}(\mathbf{x}) \leq 0 \text { for all } i \in\{1, \ldots, N\}}\end{array} xminimizef(x) subject to ci(x)≤0 for all i∈{1,…,N}
- 拉格朗日乘子法
L ( x , α ) = f ( x ) + ∑ i α i c i ( x ) where α i ≥ 0 L(\mathbf{x}, \alpha)=f(\mathbf{x})+\sum_{i} \alpha_{i} c_{i}(\mathbf{x}) \text { where } \alpha_{i} \geq 0 L(x,α)=f(x)+∑iαici(x) where αi≥0
- 惩罚项
欲使 c i ( x ) ≤ 0 c_i(x) \leq 0 ci(x)≤0,将项 α i c i ( x ) \alpha_ic_i(x) αici(x)加入目标函数,如多层感知机章节中的 λ 2 ∣ ∣ w ∣ ∣ 2 \frac{\lambda}{2} ||w||^2 2λ∣∣w∣∣2
- 投影
Proj X ( x ) = argmin x ′ ∈ X ∥ x − x ′ ∥ 2 \operatorname{Proj}_{X}(\mathbf{x})=\underset{\mathbf{x}^{\prime} \in X}{\operatorname{argmin}}\left\|\mathbf{x}-\mathbf{x}^{\prime}\right\|_{2} ProjX(x)=x′∈Xargmin∥x−x′∥2
- 梯度下降
- 一维梯度下降
- 沿梯度反方向移动自变量可以减小函数值
泰勒展开:
f ( x + ϵ ) = f ( x ) + ϵ f ′ ( x ) + O ( ϵ 2 ) f(x+\epsilon)=f(x)+\epsilon f^{\prime}(x)+\mathcal{O}\left(\epsilon^{2}\right) f(x+ϵ)=f(x)+ϵf′(x)+O(ϵ2)
代入沿梯度方向的移动量 η f ′ ( x ) \eta f^{\prime}(x) ηf′(x):
f ( x − η f ′ ( x ) ) = f ( x ) − η f ′ 2 ( x ) + O ( η 2 f ′ 2 ( x ) ) f\left(x-\eta f^{\prime}(x)\right)=f(x)-\eta f^{\prime 2}(x)+\mathcal{O}\left(\eta^{2} f^{\prime 2}(x)\right) f(x−ηf′(x))=f(x)−ηf′2(x)+O(η2f′2(x))
f ( x − η f ′ ( x ) ) ≲ f ( x ) f\left(x-\eta f^{\prime}(x)\right) \lesssim f(x) f(x−ηf′(x))≲f(x)
x ← x − η f ′ ( x ) x \leftarrow x-\eta f^{\prime}(x) x←x−ηf′(x)
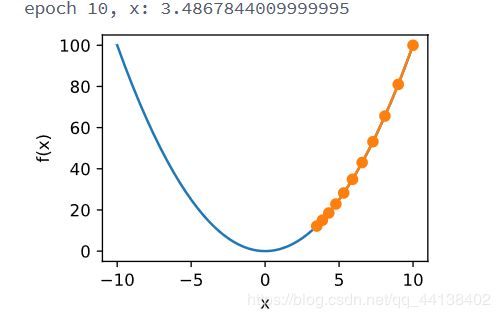
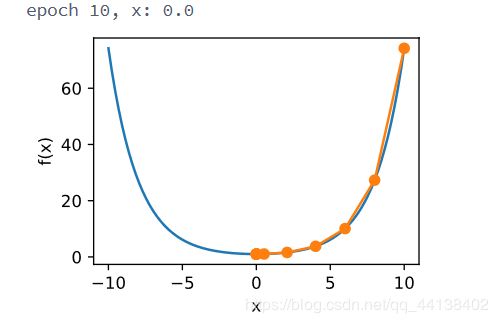
如果用 f ( x ) = x 2 f(x)=x^2 f(x)=x2作为例子
def f(x):
return x**2 # Objective function
def gradf(x):
return 2 * x # Its derivative
def gd(eta):
x = 10
results = [x]
for i in range(10):
x -= eta * gradf(x)
results.append(x)
print('epoch 10, x:', x)
return results
res = gd(0.2)
![]()
def show_trace(res):
n = max(abs(min(res)), abs(max(res)))
f_line = np.arange(-n, n, 0.01)
d2l.set_figsize((3.5, 2.5))
d2l.plt.plot(f_line, [f(x) for x in f_line],'-')
d2l.plt.plot(res, [f(x) for x in res],'-o')
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)')
show_trace(res)
- 学习率
show_trace(gd(0.05))
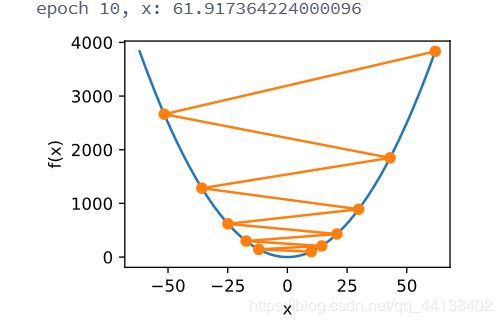
show_trace(gd(1.1))
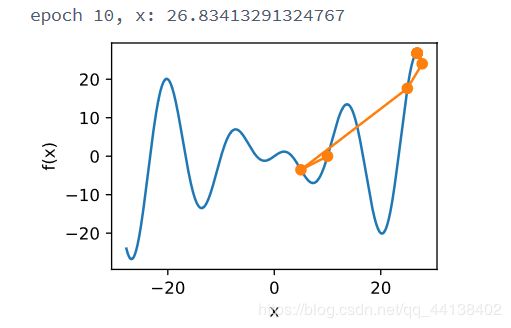
- 局部极小值
c = 0.15 * np.pi
def f(x):
return x * np.cos(c * x)
def gradf(x):
return np.cos(c * x) - c * x * np.sin(c * x)
show_trace(gd(2))
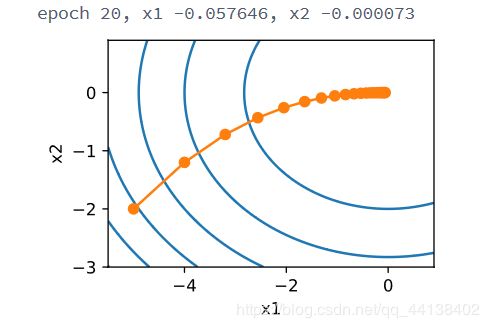
- 多维梯度下降
eta = 0.1
def f_2d(x1, x2): # 目标函数
return x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2):
return (x1 - eta * 2 * x1, x2 - eta * 4 * x2)
show_trace_2d(f_2d, train_2d(gd_2d))
- 自适应方法
- 牛顿法
f ( x ) = x 2 f(x)=x^2 f(x)=x2在 x + ϵ x+\epsilon x+ϵ处泰勒展开:
f ( x + ϵ ) = f ( x ) + ϵ ⊤ ∇ f ( x ) + 1 2 ϵ ⊤ ∇ ∇ ⊤ f ( x ) ϵ + O ( ∥ ϵ ∥ 3 ) f(\mathbf{x}+\epsilon)=f(\mathbf{x})+\epsilon^{\top} \nabla f(\mathbf{x})+\frac{1}{2} \epsilon^{\top} \nabla \nabla^{\top} f(\mathbf{x}) \epsilon+\mathcal{O}\left(\|\epsilon\|^{3}\right) f(x+ϵ)=f(x)+ϵ⊤∇f(x)+21ϵ⊤∇∇⊤f(x)ϵ+O(∥ϵ∥3)
最小值点处保证 ∇ f ( x ) = 0 \nabla{f(x)}=0 ∇f(x)=0这也就是说,需要满足 ∇ f ( x + ϵ ) = 0 \nabla{f(x+\epsilon)}=0 ∇f(x+ϵ)=0
,对上式关于 ϵ \epsilon ϵ求偏导,如果忽略高阶无穷小有:
∇ f ( x ) + H f ϵ = 0 and hence ϵ = − H f − 1 ∇ f ( x ) \nabla f(\mathbf{x})+\boldsymbol{H}_{f} \boldsymbol{\epsilon}=0 \text { and hence } \epsilon=-\boldsymbol{H}_{f}^{-1} \nabla f(\mathbf{x}) ∇f(x)+Hfϵ=0 and hence ϵ=−Hf−1∇f(x)
c = 0.5
def f(x):
return np.cosh(c * x) # Objective
def gradf(x):
return c * np.sinh(c * x) # Derivative
def hessf(x):
return c**2 * np.cosh(c * x) # Hessian
# Hide learning rate for now
def newton(eta=1):
x = 10
results = [x]
for i in range(10):
x -= eta * gradf(x) / hessf(x)
results.append(x)
print('epoch 10, x:', x)
return results
show_trace(newton())
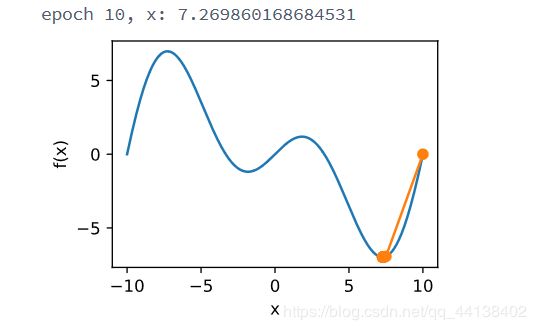
c = 0.15 * np.pi
def f(x):
return x * np.cos(c * x)
def gradf(x):
return np.cos(c * x) - c * x * np.sin(c * x)
def hessf(x):
return - 2 * c * np.sin(c * x) - x * c**2 * np.cos(c * x)
show_trace(newton())
show_trace(newton(0.5))
- 收敛性分析
只考虑在函数为凸函数, 且最小值点上 f ′ ′ ( x ∗ ) > 0 f''(x^*) > 0 f′′(x∗)>0时的收敛速度:
令 x k x_k xk为第 k k k次迭代后 x x x的值, e k : = x k − x ∗ e_{k}:=x_{k}-x^{*} ek:=xk−x∗表示 到最小值点 x ∗ x^* x∗的距离,由 f ′ ( x ∗ ) = 0 f'(x^*)=0 f′(x∗)=0:
0 = f ′ ( x k − e k ) = f ′ ( x k ) − e k f ′ ′ ( x k ) + 1 2 e k 2 f ′ ′ ′ ( ξ k ) for some ξ k ∈ [ x k − e k , x k ] 0=f^{\prime}\left(x_{k}-e_{k}\right)=f^{\prime}\left(x_{k}\right)-e_{k} f^{\prime \prime}\left(x_{k}\right)+\frac{1}{2} e_{k}^{2} f^{\prime \prime \prime}\left(\xi_{k}\right) \text{for some } \xi_{k} \in\left[x_{k}-e_{k}, x_{k}\right] 0=f′(xk−ek)=f′(xk)−ekf′′(xk)+21ek2f′′′(ξk)for some ξk∈[xk−ek,xk]
两边除以 f ′ ′ ( x k ) f''(x_k) f′′(xk),有:
e k − f ′ ( x k ) / f ′ ′ ( x k ) = 1 2 e k 2 f ′ ′ ′ ( ξ k ) / f ′ ′ ( x k ) e_{k}-f^{\prime}\left(x_{k}\right) / f^{\prime \prime}\left(x_{k}\right)=\frac{1}{2} e_{k}^{2} f^{\prime \prime \prime}\left(\xi_{k}\right) / f^{\prime \prime}\left(x_{k}\right) ek−f′(xk)/f′′(xk)=21ek2f′′′(ξk)/f′′(xk)
代入更新方程 x k + 1 = x k − f ′ ( x k ) / f ′ ′ ( x k ) x_{k+1} = x_{k} - f^{\prime}\left(x_{k}\right) / f^{\prime \prime}\left(x_{k}\right) xk+1=xk−f′(xk)/f′′(xk), 得到:
x k − x ∗ − f ′ ( x k ) / f ′ ′ ( x k ) = 1 2 e k 2 f ′ ′ ′ ( ξ k ) / f ′ ′ ( x k ) x_k - x^{*} - f^{\prime}\left(x_{k}\right) / f^{\prime \prime}\left(x_{k}\right) =\frac{1}{2} e_{k}^{2} f^{\prime \prime \prime}\left(\xi_{k}\right) / f^{\prime \prime}\left(x_{k}\right) xk−x∗−f′(xk)/f′′(xk)=21ek2f′′′(ξk)/f′′(xk)
x k + 1 − x ∗ = e k + 1 = 1 2 e k 2 f ′ ′ ′ ( ξ k ) / f ′ ′ ( x k ) x_{k+1} - x^{*} = e_{k+1} = \frac{1}{2} e_{k}^{2} f^{\prime \prime \prime}\left(\xi_{k}\right) / f^{\prime \prime}\left(x_{k}\right) xk+1−x∗=ek+1=21ek2f′′′(ξk)/f′′(xk)
当 1 2 f ′ ′ ′ ( ξ k ) / f ′ ′ ( x k ) ≤ c \frac{1}{2} f^{\prime \prime \prime}\left(\xi_{k}\right) / f^{\prime \prime}\left(x_{k}\right) \leq c 21f′′′(ξk)/f′′(xk)≤c时,有:
e k + 1 ≤ c e k 2 e_{k+1} \leq c e_{k}^{2} ek+1≤cek2
- 预处理(Heissan阵辅助梯度下降)
x ← x − η diag ( H f ) − 1 ∇ x \mathbf{x} \leftarrow \mathbf{x}-\eta \operatorname{diag}\left(H_{f}\right)^{-1} \nabla \mathbf{x} x←x−ηdiag(Hf)−1∇x
- 梯度下降和线性搜索(共轭梯度法)
- 随机梯度下降
- 随机梯度下降参数更新
对于有 n n n个样本对训练数据集,设 f i ( x ) f_i(x) fi(x)是第 i i i个样本的损失函数, 则目标函数为:
f ( x ) = 1 n ∑ i = 1 n f i ( x ) f(\mathbf{x})=\frac{1}{n} \sum_{i=1}^{n} f_{i}(\mathbf{x}) f(x)=n1∑i=1nfi(x)
其梯度为:
∇ f ( x ) = 1 n ∑ i = 1 n ∇ f i ( x ) \nabla f(\mathbf{x})=\frac{1}{n} \sum_{i=1}^{n} \nabla f_{i}(\mathbf{x}) ∇f(x)=n1∑i=1n∇fi(x)
使用该梯度的一次更新的时间复杂度为 O ( n ) \mathcal{O}(n) O(n)
随机梯度下降更新公式 O ( 1 ) \mathcal{O}(1) O(1):
x ← x − η ∇ f i ( x ) \mathbf{x} \leftarrow \mathbf{x}-\eta \nabla f_{i}(\mathbf{x}) x←x−η∇fi(x)
且有:
E i ∇ f i ( x ) = 1 n ∑ i = 1 n ∇ f i ( x ) = ∇ f ( x ) \mathbb{E}_{i} \nabla f_{i}(\mathbf{x})=\frac{1}{n} \sum_{i=1}^{n} \nabla f_{i}(\mathbf{x})=\nabla f(\mathbf{x}) Ei∇fi(x)=n1∑i=1n∇fi(x)=∇f(x)
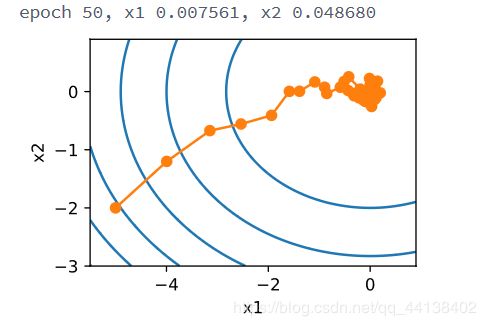
举个例子,例如函数 f ( x 1 , x 2 ) = x 1 2 + 2 x 2 2 f(x_1,x_2)=x_1^2+2x_2^2 f(x1,x2)=x12+2x22
def f(x1, x2):
return x1 ** 2 + 2 * x2 ** 2 # Objective
def gradf(x1, x2):
return (2 * x1, 4 * x2) # Gradient
def sgd(x1, x2): # Simulate noisy gradient
global lr # Learning rate scheduler
(g1, g2) = gradf(x1, x2) # Compute gradient
(g1, g2) = (g1 + np.random.normal(0.1), g2 + np.random.normal(0.1))
eta_t = eta * lr() # Learning rate at time t
return (x1 - eta_t * g1, x2 - eta_t * g2) # Update variables
eta = 0.1
lr = (lambda: 1) # Constant learning rate
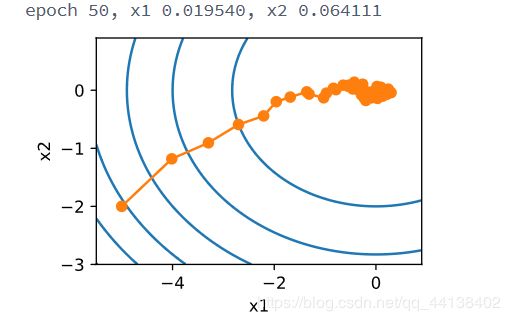
show_trace_2d(f, train_2d(sgd, steps=50))
- 动态学习率
def exponential():
global ctr
ctr += 1
return math.exp(-0.1 * ctr)
ctr = 1
lr = exponential # Set up learning rate
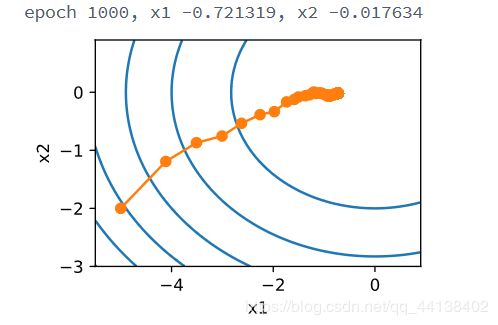
show_trace_2d(f, train_2d(sgd, steps=1000))
def polynomial():
global ctr
ctr += 1
return (1 + 0.1 * ctr)**(-0.5)
ctr = 1
lr = polynomial # Set up learning rate
show_trace_2d(f, train_2d(sgd, steps=50))
- 小批量随机梯度下降
- 从零开始实现
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net, loss = d2l.linreg, d2l.squared_loss
w = torch.nn.Parameter(torch.tensor(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=torch.float32),
requires_grad=True)
b = torch.nn.Parameter(torch.zeros(1, dtype=torch.float32), requires_grad=True)
def eval_loss():
return loss(net(features, w, b), labels).mean().item()
ls = [eval_loss()]
data_iter = torch.utils.data.DataLoader(
torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
l = loss(net(X, w, b), y).mean() # 使用平均损失
# 梯度清零
if w.grad is not None:
w.grad.data.zero_()
b.grad.data.zero_()
l.backward()
optimizer_fn([w, b], states, hyperparams) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
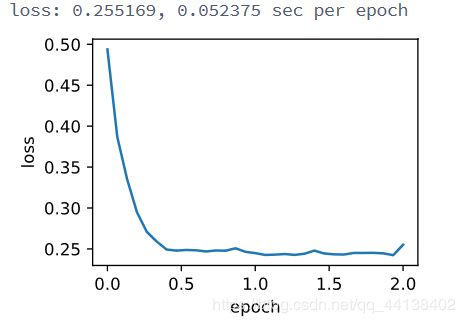
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
d2l.set_figsize()
d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
d2l.plt.xlabel('epoch')
d2l.plt.ylabel('loss')
def train_sgd(lr, batch_size, num_epochs=2):
train_ch7(sgd, None, {'lr': lr}, features, labels, batch_size, num_epochs)
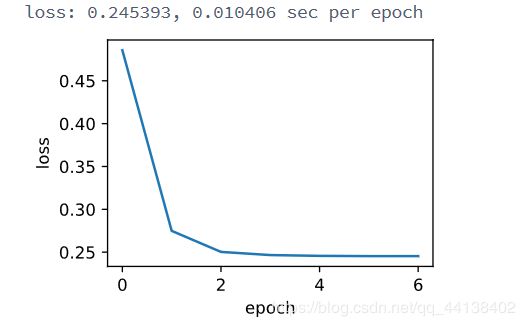
train_sgd(1, 1500, 6)
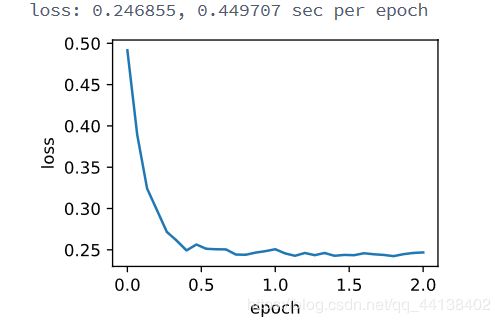
train_sgd(0.005, 1)
train_sgd(0.05, 10)
- 简洁实现
# 本函数与原书不同的是这里第一个参数优化器函数而不是优化器的名字
# 例如: optimizer_fn=torch.optim.SGD, optimizer_hyperparams={"lr": 0.05}
def train_pytorch_ch7(optimizer_fn, optimizer_hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net = nn.Sequential(
nn.Linear(features.shape[-1], 1)
)
loss = nn.MSELoss()
optimizer = optimizer_fn(net.parameters(), **optimizer_hyperparams)
def eval_loss():
return loss(net(features).view(-1), labels).item() / 2
ls = [eval_loss()]
data_iter = torch.utils.data.DataLoader(
torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
# 除以2是为了和train_ch7保持一致, 因为squared_loss中除了2
l = loss(net(X).view(-1), y) / 2
optimizer.zero_grad()
l.backward()
optimizer.step()
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss())
# 打印结果和作图
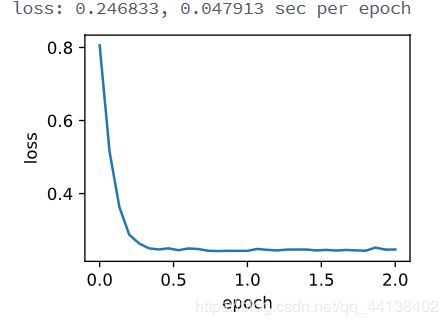
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
d2l.set_figsize()
d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
d2l.plt.xlabel('epoch')
d2l.plt.ylabel('loss')
train_pytorch_ch7(optim.SGD, {"lr": 0.05}, features, labels, 10)