关系模型的基本概念
一、关系模型的三要素:
- 关系数据结构:关系模型中只包含单一的数据结构----关系,在用户看来关系模型中数据的逻辑结构是一张扁平的二维表
- 关系操作(操作对象和结果都是集合):
- 查询:选择、投影、连接、并、差、交、笛卡尔积
- 更新(插入、删除、修改)
- 关系的完整性约束:
-
实体完整性:主属性不能为空,主码不相等
-
参照完整性:例如,学生(学号、姓名、专业号),专业(专业号,专业名),学生关系中的专业号需要参照专业关系中的专业号,称学生关系中的专业号是学生关系的外码,专业关系是被参照关系,学生关系为参照关系,外码与主码不一定要同名,学生关系中的外码取值要么为空值,要么为专业关系中对应专业号的值
-
用户定义完整性:例如,学生的成绩取值范围在0~100之间
-
二、关系中涉及的基本概念
域:一组具有相同数据类型的值的集合,例如:{0,1}、{男,女}
笛卡尔积:域上的一种集合运算,可表示为一张二维表,表中的每一行表示元组,每一列来自一个域
例如:给出三个域,D1=导师集合{t1,t2},D2=专业集合={z1,z2},D3=研究生集合={s1,s2,s3},则
D1、D2、D3的笛卡尔积为D1*D2*D3={(t1,z1,s1)(t1,z1,s2)(t1,z1,s3)(t1,z2,s1)(t1,z2,s2)(t1,z2,s3)(t2,z1,s1)(t2,z1,s2)(t2,z1,s3)(t2,z2,s1)(t2,z2,s2)(t2,z2,s3)},其中(t1,z1,s1)、(t1,z2,s2)等都是元组,t1、z2、s1、s2等都是分量
该笛卡尔积的基数为各个域的基数相乘即:2*2*3=12
| 导师 | 专业 | 研究生 |
|---|---|---|
| t1 | z1 | s1 |
| t1 | z1 | s2 |
| t1 | z1 | s3 |
| t1 | z2 | s1 |
| t1 | z2 | s2 |
| t1 | z2 | s3 |
| t2 | z1 | s1 |
| t2 | z1 | s2 |
| t2 | z1 | s3 |
| t2 | z2 | s1 |
| t2 | z2 | s2 |
| t2 | z2 | s3 |
关系:笛卡尔积(D1D2...*Dn)的有限子集叫做在域D1,D2,...,Dn上的关系,表示为R(D1,D2,...,Dn),其中R为关系的名字,n为关系的目或度,关系也是一张二维表,表中的每行对应一个元组,每列对应一个域,列的名字称为属性,n目关系必有n个属性,n=1时称该关系为单元关系/一元关系,n=2时称该关系为二元关系
候选码:某一属性组的值能唯一地标识一个元组,而其子集不能的属性组
主码:若一个关系有多个候选码,则选定一个作为主码
主属性:候选码的诸属性
非主属性(非码属性):不包含任何候选码中的属性
全码:关系模式的所有属性是这个关系模式的候选码
三、关系的三种类型:
基本关系(基本表/基表):是实际存在的表,是实际存储数据的逻辑表示
查询表:查询结果对应的表
视图表:由基本表或其他视图表导出的表,是虚表,不对应实际存储的数据
四、基本关系具有的性质:
(1)列是同质的,即每一列中的分量是同一类型的数据,来自同一个域
(2)不同的列可出自同一个域,称其中的每一列为一个属性,不同的属性要给予不同的属性名
(3)列的顺序无所谓,行的顺序无所谓
(4)任意两个元组的候选码不能取相同的值
(5)分量必须是原子值,及每一个分量都必须是不可再分的数据项
五、关系代数:
定义:是一种抽象的查询语言,用对关系的运算来表达查询
三要素:
运算对象(关系)
运算符:
传统的集合运算:
并(去掉重复的元组)、交、差、笛卡尔积
专门的关系运算:
选择(行):例如,查询IS系的全体学生, ![]()
投影(列):例如,查询学生的姓名和所在系(有重复行去除重复行),![]()
连接(也叫θ链接):A和B分别为R和S上列数相等且可比的属性组,θ为比较运算符,连接运算从R和S的 笛卡尔积R*S中选取在A属性组上的值与S关系在B属性组上的值满足比较关系θ的元组
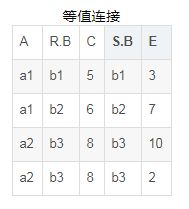
等值连接:“θ=0”时的连接
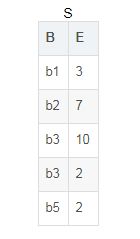
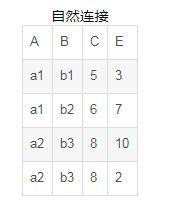
自然连接:特殊的等值连接,即在等值连接的基础上去掉重复的列,例如:
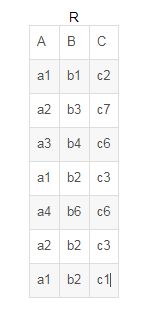
除:例如,设关系R、S如下图所示则R÷S:
在关系R中,A可以取4个值{a1,a2,a3,a4},其中
a1的象集为{(b1,c2),(b2,c3),(b2,c1)},a2的象集为{(b3,c7),(b2,c3)}
a3的象集为{(b4,c6)},a4的象集为{(c6,c6)}
S在(B,C)上的投影为{(b1,c2)(b2,c1)(b2,c3)},显然只有a1的象集包含了S在(B,C)属 性组上的投影,所以R÷S={a1}
运算结果(关系)