最大熵模型（ME）和最大熵马尔可夫模型（MEMM）

最大熵模型（Maximum Entropy Model, MEM）

最大熵思想

无更多信息的情况下，最随机的推断（概率分布的熵最大）是最合理的推断，即未知部分均匀分布时最合理，均匀分布的熵最大。若基于判别模型$P(y|\mathbf{x})$预测实例类别，无先验知识下，实例$\mathbf{x}$应等可能属于各类别，即
$$P(c_1|\mathbf{x})=P(c_2|\mathbf{x})=\cdots =P(c_K|\mathbf{x})=1/K$$
对于带有约束的情况，如$X$取值集合为$\{a,b,c,d,e\}$，约束$P(a)+P(b)=1/3$，则
$$P(a)=P(b)=1/6,P(c)=P(d)=P(e)=2/9$$

时，概率分布的熵最大，最大熵模型的思想就是寻找满足约束且熵最大的模型。

最大熵模型表示

令$\nu (\mathbf{x},y)$表示训练样本集中$(\mathbf{x},y)$出现的频数，以频数估计经验分布
$$\hat{P}(\mathbf{x},y)=\frac{\nu (\mathbf{x},y)}{N},\hat{P}(\mathbf{x})=\frac{\nu (\mathbf{x})}{N}\text{\hspace{1em}(1)}$$

定义二值特征函数$f(\mathbf{x},y)$，表示输入输出之间的事实关系，即
$$f(\mathbf{x},y)=\{\begin{array}{ll}1,& \mathbf{x}与y满足某一事实\\ 0,& 其他\end{array}$$
理想的模型应能获取训练集中的约束信息，即特征函数在模型分布、经验分布熵的期望近似，即
$${\mathbb{E}}_{\hat{P}}(f)\approx {\mathbb{E}}_P(f)⟹\sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)f(\mathbf{x},y)\approx \sum _{\mathbf{x},y}P(\mathbf{x},y)f(\mathbf{x},y)$$
最大熵模型的学习，等价于最大化带有约束的条件熵：
$$\begin{array}{rl}\underset{P}{\min }& -H(P)=-H(Y|X)=\sum _{\mathbf{x},y}P(\mathbf{x},y)\log P(y|\mathbf{x})\\ \text{s.t.}& E_{\hat{p}}(f_i)=E_p(f_i),i=1,\cdots ,k\\ & \sum _{y}P(y|\mathbf{x})=1\end{array}$$

判别式模型无法得到$P(\mathbf{x},y)$的分布，使用近似$P(\mathbf{x},y)\approx P(y|\mathbf{x})\hat{P}(\mathbf{x})$。最大熵模型根据特征函数，将训练集划分成已知信息和未知信息两类，每一个特征函数对应一种二划分。

最大熵模型学习

构造拉格朗日函数，求解约束极值问题
$$L(P,\mathbf{w})=\sum _{\mathbf{x},y}P(y|\mathbf{x})\hat{P}(\mathbf{x})\log P(y|\mathbf{x})+w_0\left(1-\sum _{y}P(y|\mathbf{x})\right)+\sum _i{w}_i\left(\sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)f_i(\mathbf{x},y)-\sum _{\mathbf{x},y}P(y|\mathbf{x})\hat{P}(\mathbf{x})f_i(\mathbf{x},y)\right)$$
由于$L$是$P$的凸函数，故原始问题的解与对偶问题的解等价：
$$\underset{P}{\min }\underset{\mathbf{w}}{\max }L(P,\mathbf{w})⟺\underset{\mathbf{w}}{\max }\underset{P}{\min }L(P,\mathbf{w})$$

I. 求内部极小（导出最大熵模型）： 令$L$对$P(\mathbf{x}|y)$的偏导为0，且假设$\hat{P}(\mathbf{x})>0$，则
$$\sum _{\mathbf{x},y}\tilde{P}(\mathbf{x})\left(\log P(y|\mathbf{x})+1-w_0-\sum _i{w}_i{f}_i(\mathbf{x},y)\right)=0⟹P(y|\mathbf{x})=\frac{\exp \left({\sum }_i{w}_i{f}_i(\mathbf{x},y)\right)}{\exp (1-w_0)}$$
根据约束条件知：${\sum }_{y}P(y|x)=1$，执行归一化也可以进一步消去$w_0$，最终得最大熵模型
$$P_w(y|\mathbf{x})=\frac{1}{Z_{\mathbf{w}}(\mathbf{x})}\exp \left(\sum _i{w}_i{f}_i(\mathbf{x},y)\right),Z_{\mathbf{w}}(\mathbf{x})=\sum _y\exp \left(\sum _i{w}_i{f}_i(\mathbf{x},y)\right)\text{\hspace{1em}(2)}$$
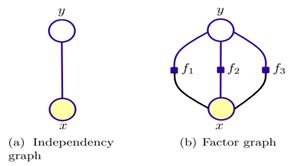
从最大熵模型的表达式可知，最大熵模型将复杂的联合分布分解为多个指数项/因子的乘积，得到给定$x$下$y$的条件概率分布。

II. 求外部极大（用于更新最大熵模型$P_w$的参数）： 将内部极小结果带入拉格朗日函数，得
$$\phi (\mathbf{w})=\sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)\sum _i{w}_i{f}_i(\mathbf{x},y)-\sum _{\mathbf{x}}\hat{P}(\mathbf{x})\log Z_{\mathbf{w}}(\mathbf{x})$$

则$\hat{\mathbf{w}}=\arg {\max }_{\mathbf{w}}\phi (\mathbf{w})$，参数学习使用改进的迭代尺度算法IIS求解。

最大熵模型求解过程举例

假设随机变量X有5个取值，约束 P(A)+P(B)=3/10，估计随机变量各个取值的概率。

该问题的最大熵模型的拉格朗日函数为
$$L(P)=\sum _{i=1}^{5}P(y_i)\log P(y_i)+w_i\left(P(y_i)+P(y_2)-\frac{3}{10}\right)+w_0\left(\sum _{i=1}^{5}P(y_i)-1\right)$$

根据内部极小，得到
$$P_w(y_1)=P_w(y_2)=\frac{e^{w_1}}{2e^{w_1}+3},P(y_3)=P(y_4)=P(y_5)=\frac{1}{2e^{w_1}+3}$$

根据外部极大，得到
$$\phi (w)=\frac{3}{10}{w}_1-\log (2e^{w_1}+3)$$

对$\phi (w)$求$w$的偏导令其为0，得
$$e^{w_1}=\frac{9}{14}⟹P(y_1)=P(y_2)=\frac{3}{20},P(y_3)=P(y_4)=P(y_5)=\frac{7}{30}$$
李航《统计学习》上有未归一化内部极小得到的最大熵模型的解法。

最大熵模型与极大似然估计

判别模型的极大似然估计
$$\begin{array}{rl}L(\mathbf{w})& =\prod _{i,j}P(y_j|{\mathbf{x}}_i,\mathbf{w})\hat{P}({\mathbf{x}}_i)=\prod _{\mathbf{x},y}[P(y|\mathbf{x},\mathbf{w})\hat{P}(\mathbf{x}){]}^{\nu (\mathbf{x},y)}\\ & \simeq \prod _{\mathbf{x},y}[P(y|\mathbf{x},\mathbf{w})\hat{P}(\mathbf{x}){]}^{\frac{\nu (\mathbf{x},y)}{N}}=\prod _{\mathbf{x},y}[P(y|\mathbf{x},\mathbf{w})\hat{P}(\mathbf{x}){]}^{\hat{P}(\mathbf{x},y)}\\ & \simeq \sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)\log P(y|\mathbf{x},\mathbf{w})+\hat{P}(\mathbf{x},y)\log \hat{P}(\mathbf{x})\\ & \simeq \sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)\log P(y|\mathbf{x},\mathbf{w})\end{array}$$

其中$\nu (\mathbf{x},y)$表示样本$(\mathbf{x},y)$的频数，${\sum }_{\mathbf{x},y}$是对样本集中不重复样本$(\mathbf{x},y)$求和。

从上式可得，极大对数似然估计与最大熵模型目标函数的区别在于log前是经验联合分布还是模型联合分布，由于最大熵模型使用约束“经验联合分布近似于模型联合分布”，因此极大似然估计与基于约束的最大熵模型描述的问题基本一致。

将公式(1)(2)带入上式，也可以得到两者的等价关系
$$L(\mathbf{w})=\sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)\sum _i{w}_i{f}_i(\mathbf{x},y)-\sum _{\mathbf{x}}\hat{P}(\mathbf{x})\log Z_{\mathbf{w}}(\mathbf{x})=\phi (\mathbf{w})$$

即 最大熵对偶函数的极大化等价于最大熵模型的极大似然估计。

最大熵模型与逻辑回归

根据最大熵模型内部极小问题得到的条件概率分布，并定义特征函数，则
$$P(y|\mathbf{x},\mathbf{w})=\frac{\exp (\mathbf{w}\cdot f(\mathbf{x},y))}{{\sum }_y\exp (\mathbf{w}\cdot f(\mathbf{x},y))},f(\mathbf{x},y)=\{\begin{array}{ll}\mathbf{x},& y=1\\ 0,& y=0\end{array}$$

由最大熵模型可推出逻辑回归模型
$$P(y=1|\mathbf{x},\mathbf{w})=\frac{e^{\mathbf{w}\cdot \mathbf{x}}}{1+e^{\mathbf{w}\cdot \mathbf{x}}}=\frac{1}{1+e^{-\mathbf{w}\cdot \mathbf{x}}}$$
ME和LR模型类似，称之为对数线性模型，模型学习就是在给定训练数据条件下进行极大似然估计。

模型学习之改进的迭代尺度法（Improved Iterative Scaling，IIS）

改进的迭代尺度法基本思想是，寻找新的参数向量$\mathbf{w}+\mathbf{\delta }=(w_1+{\delta }_1,\cdots ,w_n+{\delta }_n{)}^T$使得似然函数下界增大，从而提高似然函数的值，直至似然函数达到最大值.

当$a>0$时，由$-\log a\ge 1-a$，则模型参数从$\mathbf{w}$变化为$\mathbf{w}+\mathbf{\delta }$，似然函数变化
$$\begin{array}{rl}L(\mathbf{w}+\mathbf{\delta })-L(\mathbf{w})& =\sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)\sum _i{\delta }_i{f}_i(\mathbf{x},y)-\sum _{\mathbf{x}}\hat{P}(\mathbf{x})\log \frac{Z_{\mathbf{w}+\mathbf{\delta }}(\mathbf{x})}{Z_{\mathbf{w}}(\mathbf{x})}\\ & \ge \sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)\sum _i{\delta }_i{f}_i(\mathbf{x},y)+1-\sum _{\mathbf{x}}\hat{P}(\mathbf{x})\frac{Z_{\mathbf{w}+\mathbf{\delta }}(\mathbf{x})}{Z_{\mathbf{w}}(\mathbf{x})}\\ & =\sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)\sum _i{\delta }_i{f}_i(\mathbf{x},y)+1-\sum _{\mathbf{x}}\hat{P}(\mathbf{x})\sum _y{P}_{\mathbf{w}}(y|\mathbf{x})\exp \sum _i{\delta }_i{f}_i(\mathbf{x},y)\end{array}$$

IIS算法试图每次只优化一个${\delta }_i$，固定其它${\delta }_j$. 引入变量$f^{\#}(\mathbf{x},y)={\sum }_k{f}_k(\mathbf{x},y)$，由Jensen不等式知
$$\exp \left(\sum _i{\delta }_i{f}_i(\mathbf{x},y)\right)=\exp \left(\sum _i\frac{f_i(\mathbf{x},y)}{f^{\#}(\mathbf{x},y)}{\delta }_i{f}^{\#}(\mathbf{x},y)\right)\le \sum _i\frac{f_i(\mathbf{x},y)}{f^{\#}(\mathbf{x},y)}\exp ({\delta }_i{f}^{\#}(\mathbf{x},y))$$

省略常数项，并记$P_{\mathbf{w}}(\mathbf{x},y)=\hat{P}(\mathbf{x})P_{\mathbf{x}}(y|\mathbf{x})$，因此
$$\begin{array}{rl}L(\mathbf{w}+\mathbf{\delta })-L(\mathbf{w})& \ge \sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)\sum _i{\delta }_i{f}_i(\mathbf{x},y)-\sum _{\mathbf{x},y}{P}_{\mathbf{w}}(\mathbf{x},y)\exp \sum _i{\delta }_i{f}_i(\mathbf{x},y)\\ & \ge \sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)\sum _i{\delta }_i{f}_i(\mathbf{x},y)-\sum _{\mathbf{x},y}{P}_{\mathbf{w}}(\mathbf{x},y)\sum _i\frac{f_i(\mathbf{x},y)}{f^{\#}(\mathbf{x},y)}\exp ({\delta }_i{f}^{\#}(\mathbf{x},y))=B(\mathbf{\delta }|\mathbf{w})\end{array}$$

求$B$对${\delta }_i$并令其为0，得
$$\sum _{\mathbf{x},y}{P}_{\mathbf{w}}(\mathbf{x},y)f_i(\mathbf{x},y)\exp ({\delta }_i{f}^{\#}(\mathbf{x},y))=\sum _{\mathbf{x},y}\hat{P}(\mathbf{x},y)f_i(\mathbf{x},y)$$

若对于任意$(\mathbf{x},y)$，$f^{\#}(\mathbf{x},y)$为常数$M$，则${\delta }_i$显式表示为
$${\delta }_i=\frac{1}{M}\log \frac{E_{\hat{P}}(f_i)}{E_P(f_i)}$$

否则，需通过牛顿法求解${\delta }_i$。

ME总结

优点： 可通过灵活的约束条件，调节模型对未知数据的适应度和已知数据的拟合度；最大熵模型关于数据分布的熵极大，作为经典分类模型准确度较高。
缺点： 约束函数与样本数量相关，大样本下迭代计算量巨大，实际应用困难。

最大熵马尔可夫模型（Maximum Entropy Markov Model, MEMM）

MEMM的思想是找到一个 满足马尔可夫奇次性假设、观测不独立且熵最大 的模型解决序列标注问题，模型图结构如下：

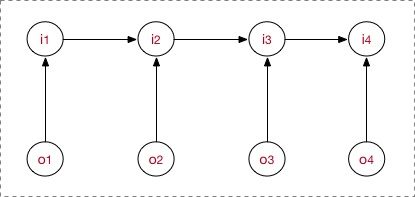
MEMM对条件概率直接建模，模型表示为
$$P(\mathbf{s}|\mathbf{o})=\prod _{t}P(s_t|s_{t-1},o_t)$$
相比HMM，MEMM没有观测独立性假设。若不考虑整个序列式，时刻$t$的隐状态可看做一个分类问题，我们采用最大熵模型建模
$$P(s_t=i|s_{t-1},o_t)=\frac{1}{Z(o_t,s_{t-1})}\exp \left(\sum _k{\lambda }_k{f}_k(o_t,s_t=i)\right),Z(o_t,s_{t-1})=\sum _i\exp \left(\sum _k{\lambda }_k{f}_k(o_t,s_t=i)\right)$$
式中，$Z(o_t,s_{t-1})$为局部归一化因子，对每时刻都需要做归一化；$f_k(o_t,s_t)$为人工定义的第$k$个二值特征函数；${\lambda }_k$为特征函数$f_k$的权重，通过训练最终确定，也是模型训练学习的唯一参数向量。

MEMM标注偏置问题

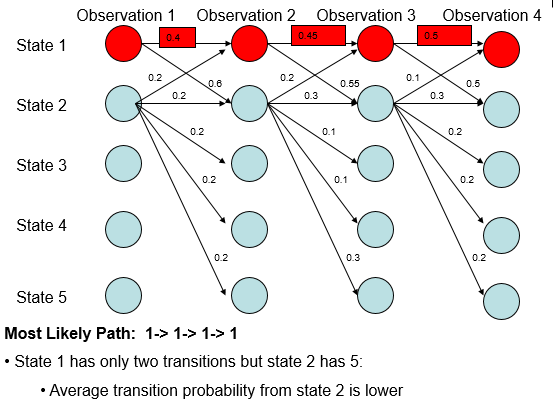
MEMM对每个时刻都做归一化（局部归一化），因此有更少转移状态的状态，其各转移概率普遍更高，因此最大概率路径更易出现转移状态少的状态.

每个节点的转移状态（分支数）不同，每个节点的转移状态形成概率分布，导致概率分布不均衡，转移状态越少的状态，转移概率（边权值）就越大，因子最终概率最大路径中更可能出现转移状态较少的状态。