深入理解计算机系统:第5-6章
第5章 优化程序性能
操作(加法或乘法)和数据类型(长整数和双精度浮点数)的不同组合,具有相同的性能。
本章对下面程序进行优化,未进行任何优化的程序运行时间约为4.2s。
#include "stdio.h"
#include "windows.h"
// 对向量所有元素求和
#define IDENT 0
#define OP +
// 计算向量元素的乘积
/*
#define IDENT 0
#define OP +
*/
typedef long data_t;
typedef struct
{
long len;
data_t *data;
} vec_rec, *vec_ptr;
vec_ptr new_vec(long len)
{
vec_ptr result = (vec_ptr)malloc(sizeof(vec_rec));
data_t* data = NULL;
if (!result)
return NULL;
result->len = len;
if (len > 0)
{
data = (data_t *)calloc(len, sizeof(data_t));
if (!data)
{
free((void*)result);
return NULL;
}
}
result->data = data;
return result;
}
int get_vec_element(vec_ptr v, long index, data_t* dest)
{
if (index < 0 || index >= v->len)
return 0;
*dest = v->data[index];
return 1;
}
long vec_length(vec_ptr v)
{
return v->len;
}
void print_time() {
SYSTEMTIME sys;
GetLocalTime(&sys);
printf("%d %d \n", sys.wSecond, sys.wMilliseconds);
}
void combine1(vec_ptr v, data_t *dest)
{
long i;
*dest = IDENT;
for (i = 0; i < vec_length(v); ++i)
{
data_t val;
get_vec_element(v, i, &val);
*dest = *dest OP val;
}
}
int main()
{
long len = 100000000;
vec_ptr v = new_vec(len);
data_t dest;
for (int i = 0; i < len; ++i)
v->data[i] = i;
print_time();
combine1(v, &dest);
print_time();
system("pause");
}
5.4 消除循环的低效率
代码移动:将计算结果不会改变的计算移动循环外部。
如下,将计算数组长度的代码移至循环外部,运行时间缩短至2.2s。
void combine2(vec_ptr v, data_t* dest)
{
*dest = IDENT;
for (long i = 0, len = vec_length(v); i < len; ++i)
{
data_t val;
get_vec_element(v, i, &val);
*dest = *dest OP val;
}
}
特别地,strlen函数时间复杂度为 O ( n ) O(n) O(n),下面未优化的版本时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
// 未优化版本
void lower1(char *s)
{
for (long i = 0; i < strlen(s); ++i)
if (s[i] >= 'A' && s[i] <= 'Z')
s[i] == ('A' - 'a');
}
// 优化版本
void lower2(char *s)
{
long length = strlen(s);
for (long i = 0; i < length; ++i)
if (s[i] >= 'A' && s[i] <= 'Z')
s[i] == ('A' - 'a');
}
5.5 减少过程调用
过程调用会带来开销(维护返回地址、局部变量等),而且妨碍大多数形式的程序优化。
重写代码,避免循坏调用过程。
下面去除循环调用过程后的优化版本,运行时间约为300ms。
data_t* get_vec_start(vec_ptr v)
{
return v->data;
}
void combine3(vec_ptr v, data_t* dest)
{
data_t* data = get_vec_start(v);
*dest = IDENT;
for (long i = 0, len = vec_length(v); i < len; ++i)
*dest = *dest OP data[i];
}
5.6 消除不必要的内存引用
对于频繁读写的内存数据,应定义局部变量减少内存访问,局部变量(立即数)存储在寄存器中,读写速度快。
如下对内存引用使用局部变量替代,但运行时间并没有提升,约为300ms。
注:性能未提升!
void combine4(vec_ptr v, data_t* dest)
{
data_t* data = get_vec_start(v);
data_t acc = IDENT;
for (long i = 0, len = vec_length(v); i < len; ++i)
acc = acc OP data[i];
*dest = acc;
}
5.8 循环展开
循环展开是一种程序变换,通过增加每次迭代计算的元素数量,减少循环的迭代次数。
如下使用2x1展开对程序进行了优化,加法运算约120ms、乘法运算约170ms。
void combine5(vec_ptr v, data_t* dest)
{
long i;
long length = vec_length(v);
long limit = length - 1;
data_t* data = get_vec_start(v);
data_t acc = IDENT;
for (i = 0; i < limit; i += 2)
acc = (acc OP data[i]) OP data[i+1];
for (; i < length; i++)
acc = acc OP data[i];
*dest = acc;
}
5.8 提高并行性
多个累积变量
对于一个可结合和可交换的合并运算(整数加法或乘法),可通过将一组合并运算分割成两个或更多的部分,并在最后合并结果来提高性能。
如
P n = ∏ i = 0 n − 1 a i P_n=\prod_{i=0}^{n-1}a_i Pn=i=0∏n−1ai
假设n为偶数,则
P n = P E n × P O n , P E n = ∏ i = 0 n / 2 − 1 a 2 i , P O n = ∏ i = 0 n / 2 − 1 a 2 i + 1 P_n=PE_n \times PO_n, \quad PE_n=\prod_{i=0}^{n/2-1}a_{2i}, \quad PO_n=\prod_{i=0}^{n/2-1}a_{2i+1} Pn=PEn×POn,PEn=i=0∏n/2−1a2i,POn=i=0∏n/2−1a2i+1
如下改进后的代码,加法运算约180ms、乘法运算约180ms。
注:性能未提升!
void combine6(vec_ptr v, data_t* dest)
{
long i;
long length = vec_length(v);
long limit = length - 1;
data_t* data = get_vec_start(v);
data_t acc0 = IDENT;
data_t acc1 = IDENT;
for (i = 0; i < limit; i += 2)
{
acc0 = acc0 OP data[i];
acc1 = acc1 OP data[i+1];
}
for (; i < length; i++)
acc0 = acc0 OP data[i];
*dest = acc0 OP acc1;
}
重新组合变换
acc = (acc OP data[i]) OP data[i+1]; 改为 acc = acc OP (data[i] OP data[i + 1]);
加法/乘法运算均约130ms。
void combine7(vec_ptr v, data_t* dest)
{
long i;
long length = vec_length(v);
long limit = length - 1;
data_t* data = get_vec_start(v);
data_t acc = IDENT;
for (i = 0; i < limit; i += 2)
acc = acc OP (data[i] OP data[i + 1]);
for (; i < length; i++)
acc = acc OP data[i];
*dest = acc;
}
5.12 理解内存性能
加载的性能
加载操作的性能既依赖于流水线能力,也依赖于加载单元的延迟。
考虑一下c代码,ls=ls->next,即变量ls的后续值依赖于指针引用ls->next读出的值。
转化为汇编指令可见,movq是循环中关键的性能瓶颈,后面的寄存器%rdi的值依赖于加载操作的结果,而加载操作有以%rdi的值作为它的地址。因此必须前一次加载操作完成,后续指令才能执行。
// c
while(ls)
{
len++;
ls = ls->next;
}
// 汇编
.L3:
addq $1, %rax
movq (%rdi), %rdi
testq %rdi, %rdi
jne .L3
存储的性能
存储操作:将寄存器值写入内存。
读写相关:一个内存读的结果依赖于 一个最近的内存写。
存储缓冲区:包含已经被发射到存储单元而又未完成存储操作的地址和数据,使得一系列存储操作不必等待每个操作都更新高速缓存就能够执行。当一个加载操作发生,若缓冲区中包含待加载地址的缓冲数据,则将该缓冲数据读取作为加载结果。
第6章 存储器层次结构
6.1 存储技术
随机访问存储器(Random-Access Memory, RAM)
静态RAM(SRAM) :双稳态存储单元,抗干扰性强,用于高速缓存器。读写快、造价高、功耗高。
动态RAM(DRAM):将每个位存储为电容的充电,对干扰非常敏感。读写慢、造价低、功耗低。
磁盘存储
磁盘容量
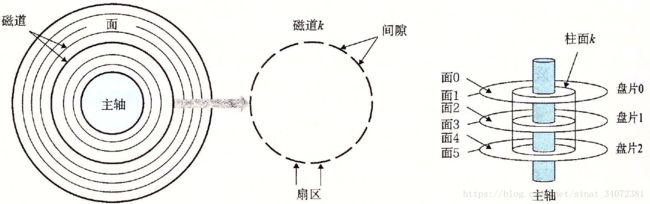
磁盘容量由记录密度、磁道密度和面密度决定。容量的计算公式如下:
磁 盘 容 量 = 字 节 数 扇 区 × 平 均 扇 区 数 磁 道 × 磁 道 数 表 面 × 表 面 数 盘 片 × 盘 片 数 磁 盘 磁盘容量=\frac{字节数}{扇区}\times\frac{平均扇区数}{磁道}\times\frac{磁道数}{表面}\times\frac{表面数}{盘片}\times\frac{盘片数}{磁盘} 磁盘容量=扇区字节数×磁道平均扇区数×表面磁道数×盘片表面数×磁盘盘片数
若一个磁盘有5个盘片,每个盘片有2个面,每个面有20000条磁道,每个磁道平均300个扇区,每个扇区512字节,则
磁 盘 容 量 = 512 字 节 扇 区 × 300 扇 区 磁 道 × 20000 磁 道 表 面 × 2 表 面 盘 片 × 5 盘 片 磁 盘 = 30720000000 字 节 = 30.72 G B \begin{aligned} 磁盘容量 & =\frac{512字节}{扇区}\times\frac{300扇区}{磁道}\times\frac{20000磁道}{表面}\times\frac{2表面}{盘片}\times\frac{5盘片}{磁盘} \\ & = 30 720 000 000 字节 \\ & = 30.72 GB \end{aligned} 磁盘容量=扇区512字节×磁道300扇区×表面20000磁道×盘片2表面×磁盘5盘片=30720000000字节=30.72GB
磁盘操作

磁盘使用读/写头来读写存储在磁性表面上的位,通过传动臂可将读/写头定位到任何磁道(寻道)。
有多个盘片的磁盘针对每个盘片有独立的读/写头,且在任何时刻,所有的读/写头都位于1个柱面上。
访问时间 = 寻道时间 + 旋转时间 + 传送时间,约为10ms。访问扇区的第一个字节耗时,后续字节几乎不耗时。
- 平均寻道时间 T a v g s e e k = 3 ∼ 9 m s T_{avg \, seek}=3 \sim 9ms Tavgseek=3∼9ms;
- 平均旋转时间 T a v g r o t a t i o n = 60 / ( 2 ∗ R P M ) T_{avg \, rotation}=60/(2*RPM) Tavgrotation=60/(2∗RPM),对于RPM为7200的磁盘, T a v g r o t a t i o n ≈ 4 m s T_{avg \, rotation}\approx 4ms Tavgrotation≈4ms;
- 平均传送时间 T a v g t r a n s f e r = 60 R P M × 1 平 均 扇 区 数 / 磁 道 {T_{avg \, transfer}=\dfrac{60}{RPM}\times\dfrac{1}{平均扇区数/磁道}} Tavgtransfer=RPM60×平均扇区数/磁道1,对于每个磁道有300个扇区、RPM为7200的磁盘, T a v g t r a n s f e r ≈ 0.03 m s T_{avg\, transfer} \approx 0.03ms Tavgtransfer≈0.03ms
对存储在SRAM的一个64位字访问时间约为4ns,对DRAM的访问时间约为60ns。故从内存中读一个512字节扇区 大小的块,SRAM约256ns、DRAM约4000ns,而磁盘约10ms。
固态硬盘
固态硬盘(Solid State Disk),是一种基于闪存的存储技术。读SSD比写快。大约100 000次重复写后,块就会损坏。
一个闪存有B个块的序列组成,每个块有P页组成,页的大小约512Bytes ~ 4KB,块是由32 ~ 128页组成,块的大小为16KB ~ 512KB。
数据以页为单位进行读写,只有在一页全部擦除之后才可写这一页,若修改某页中的内容,则必须将该页复制到新块,而且擦除时间较为耗时,故写入时间比读取时间长。
6.2 局部性
局部性,指倾向于引用邻近于其他最近引用过的数据项的数据项,或最近引用过的数据项本身。
时间局部性:被引用过一次的内存位置可能在不远的将来再次被引用;
空间局部性:若一个内存位置被引用一次,则程序很可能在不远的将来引用附近的一个内存位置。
// 良好的时间和空间局部性
int sumarrayrows(int a[M][N])
{
int i, j, sum = 0;
for (i = 0; i < M; i++)
for (j = 0; j < N; j++)
sum += a[i][j];
return sum;
}
// 局部性很差
int sumarrayrcols(int a[M][N])
{
int i, j, sum = 0;
for (j = 0; j < N; j++)
for (i = 0; i < M; i++)
sum += a[i][j];
return sum;
}
6.3 存储器层次结构
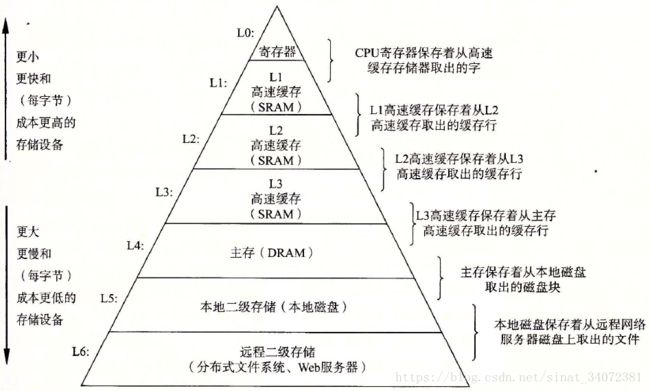
存储器层次结构中的缓存
高速缓存(cache,读作"cash"),是一个小而快速的存储设备,作为存储在更大、也更慢的设备中的数据对象的缓存区域。
对于每个k,k+1层存储器被划分层连续的数据组块,k层包含k+1层组块的子集,作为k+1层的缓存。数据以块为单位在层级间复制。
- 缓存命中
当程序需要第k+1层的数据对象d时,系统首先在缓存层(k层)查找对象d,若k层查找到d,则缓存命中。 - 缓存不命中
若未在缓存层找到所需数据对象,则缓存不命中(cache miss)。此时,k层缓存从k+1层取出包含d的数据块,根据缓存策略覆盖/驱逐现存块。如随机替换、最少使用等策略。 - 缓存不命中种类
冷缓存(k层缓存为空)不命中,称为强制性不命中或冷不命中。
冲突不命中,有限制性放置策略引起的。如k+1层分为数据块1-16,k层可缓存4块并采用放置策略为i mod 4。若CPU循环访问数据块0和8,由于数据块0和8需放置在k层同一数据块,造成每次引用都不命中。 - 缓存管理
高速缓存L1-3由硬件逻辑管理,虚拟内存由操作系统软件和CPU上的地址翻译硬件共同管理。
6.4 高速缓存存储器
通过的高速缓存存储器组织结构
S = 2 s S=2^s S=2s组,每组 E E E行,每行由1个有效位、 t t t个标记位和一个数据块 B B B( 2 b 2^b 2b字节)组成,且 m = b + s + t m = b + s + t m=b+s+t。
其中有效位指示该缓存行是否有效、标记位唯一标识缓存行(块内存地址的子集),如图4所示。

组索引的s位(无符号整数)指示缓存数据(字)必须存储的组号,t个标记位指示该数据在这个组的具体行,b个块偏移位给出数据块在B个字节中的字偏移。
6.6 综合:高速缓存对程序性能的影响
重新排列以提高空间局部性
考虑一对 n × n n \times n n×n的矩阵相乘问题,矩阵乘法通常是使用三重循环实现。
若分别使用索引i、j和k来标识,则根据循环次序的改变共计6种不同的情况。性能如下:
#define N 1000
typedef long** long_dptr;
// 约6s
void seq1(long_dptr a, long_dptr b, long_dptr c)
{
long i, j, k, sum;
for (i = 0; i < N; ++i)
for (j = 0; j < N; ++j)
{
sum = 0;
for (k = 0; k < N; ++k)
sum += (a[i][k] * b[k][j]);
c[i][j] = sum;
}
}
// 约6s
void seq2(long_dptr a, long_dptr b, long_dptr c)
{
long i, j, k, sum;
for (j = 0; j < N; ++j)
for (i = 0; i < N; ++i)
{
sum = 0;
for (k = 0; k < N; ++k)
sum += (a[i][k] * b[k][j]);
c[i][j] = sum;
}
}
// 约17s
void seq3(long_dptr a, long_dptr b, long_dptr c)
{
long i, j, k, sum, r;
for (j = 0; j < N; ++j)
for (k = 0; k < N; ++k)
{
r = b[k][j];
for (i = 0; i < N; ++i)
c[i][j] += (a[i][k] * r);
}
}
// 约17s
void seq4(long_dptr a, long_dptr b, long_dptr c)
{
long i, j, k, sum, r;
for (k = 0; k < N; ++k)
for (j = 0; j < N; ++j)
{
r = b[k][j];
for (i = 0; i < N; ++i)
c[i][j] += (a[i][k] * r);
}
}
// 约3.5s
void seq5(long_dptr a, long_dptr b, long_dptr c)
{
long i, j, k, sum, r;
for (k = 0; k < N; ++k)
for (i = 0; i < N; ++i)
{
r = a[i][k];
for (j = 0; j < N; ++j)
c[i][j] += (r * b[k][j]);
}
}
// 约3.5s
void seq6(long_dptr a, long_dptr b, long_dptr c)
{
long i, j, k, sum, r;
for (i = 0; i < N; ++i)
for (k = 0; k < N; ++k)
{
r = a[i][k];
for (j = 0; j < N; ++j)
c[i][j] += (r * b[k][j]);
}
}