后端开发面经系列 -- 字节跳动C/C++一面面经

字节跳动C/C++一面面经

公众号：阿Q技术站

来源：https://www.nowcoder.com/feed/main/detail/74bf25e202ea4fcba09c01dae530ff9b

1、虚拟地址是怎么转化到物理地址的？页表的构成？mmu了解过吗？

虚拟地址到物理地址的转换是通过操作系统中的内存管理单元（Memory Management Unit，MMU）来实现的。MMU是计算机系统中的一个硬件模块，负责虚拟地址和物理地址之间的转换。它通常采用页表的方式来管理内存。

页表的构成：

1. 页目录表（Page Directory）： 页目录表是一个二级结构，用于存储页表的基地址。每个进程有一个页目录表，它将虚拟地址的高10位映射到对应的页表。
2. 页表（Page Table）： 页表是一个二级结构，用于存储虚拟地址到物理地址的映射关系。页表的基地址存储在页目录表中。页表中的每一项对应一个页面（通常大小为4KB），存储着虚拟地址到物理地址的映射关系。

转换过程：

1. 当CPU访问内存时，会将虚拟地址发送给MMU。
2. MMU首先从虚拟地址中提取出页号，用来在页目录表中查找对应的页表基地址。
3. 接着，MMU从虚拟地址中提取出页内偏移，与查找到的页表基地址相加，得到物理地址。

C++代码，模拟虚拟地址到物理地址的转换过程：

#include 
#include 

// 假设每个页面的大小为4KB
const int PAGE_SIZE = 4096;

// 页表类
class PageTable {
public:
    // 添加映射关系
    void add_mapping(int virtual_page, int physical_page) {
        page_table[virtual_page] = physical_page;
    }

    // 获取物理地址
    int get_physical_address(int virtual_page, int offset) {
        return (page_table[virtual_page] * PAGE_SIZE) + offset;
    }

private:
    std::unordered_map page_table;
};

int main() {
    // 创建一个页表对象
    PageTable page_table;

    // 添加映射关系
    page_table.add_mapping(0, 1); // 虚拟页面0映射到物理页面1
    page_table.add_mapping(1, 2); // 虚拟页面1映射到物理页面2

    // 获取物理地址
    int virtual_page = 0;
    int offset = 1024;
    int physical_address = page_table.get_physical_address(virtual_page, offset);
    std::cout << "物理地址： " << physical_address << std::endl;

    return 0;
}

MMU的作用：

1. 地址映射： 将虚拟地址映射到物理地址，实现虚拟内存的管理。
2. 访问控制： MMU可以根据权限位（比如读、写、执行权限）控制对内存的访问。
3. 高速缓存控制： MMU可以管理处理器的高速缓存，提高内存访问速度。
4. 内存保护： MMU可以根据页表中的权限位实现内存保护，防止非法访问。

2、操作系统中的原子操作是怎么实现的？

原子操作是指不可中断的操作，要么完全执行，要么完全不执行，不会出现部分执行的情况。在操作系统中，实现原子操作通常需要硬件的支持，主要涉及以下几个方面的技术：

1. 单处理器单核系统中的实现：

   • 通过保证指令序列不被打断来实现原子性。

   • 对于简单的原子操作，CPU提供了特殊的单条指令，如INC（增量）和XCHG（交换）。

   • 对于复杂的原子操作，可能需要多条指令组合使用，并且在执行过程中需要防止上下文切换，如任务切换或中断处理，这通常通过自旋锁（spinlock）来保证操作指令序列不会在执行中途受到干扰。

2. 多处理器或多核系统中的实现：

   • 除了使用自旋锁来保证原子性外，还需要确保操作不会受到其他核心或处理器的干扰。

   • 原子操作可能需要在多个核心或处理器之间进行同步，以确保整个系统的一致性。

3. 内存屏障（Memory Barriers）：用于确保内存访问的有序性，防止编译器或硬件对指令重排序，从而影响原子操作的正确性。

4. 锁机制：如互斥锁（Mutex）和信号量（Semaphores），用于控制对共享资源的访问，确保在同一时间只有一个线程或进程可以执行特定的代码段。

5. CAS（Compare-and-Swap）操作：是一种常用于并发编程中的原子操作，它允许一个线程在没有其他线程干扰的情况下更新一个值。

6. 硬件支持：某些CPU提供了特殊的硬件指令来支持原子操作，如x86架构中的CMPXCHG指令。

7. 软件层面的封装：操作系统或编程语言提供高级抽象的同步机制，如Java中的synchronized关键字，或者C++中的std::atomic类型。

3、C++中的内存分区？bss段了解过吗？未初始化的全局变量和初始化的全局变量放在哪里？

在C++中，内存分成5个区，他们分别是栈、堆、自由存储区、全局/静态存储区和常量存储区。

• 栈，在执行函数时，函数内局部变量的存储单元都可以在栈上创建，函数执行结束时这些存储单元自动被释放。栈内存分配运算内置于处理器的指令集中，效率很高，但是分配的内存容量有限。
• 堆，就是那些由new分配的内存块，他们的释放编译器不去管，由我们的应用程序去控制，一般一个new就要对应一个delete。如果程序员没有释放掉，那么在程序结束后，操作系统会自动回收。
• 自由存储区，就是那些由malloc等分配的内存块，他和堆是十分相似的，不过它是用free来结束自己的生命的。
• 全局/静态存储区，全局变量和静态变量被分配到同一块内存中，在以前的C语言中，全局变量又分为初始化的和未初始化的，在C++里面没有这个区分了，他们共同占用同一块内存区。
• 常量存储区，这是一块比较特殊的存储区，他们里面存放的是常量，不允许修改。

对于bss段，它存放的是未初始化的全局变量和静态变量。在程序加载时，操作系统会分配一块内存给bss段，其中的变量会被初始化为0或者空指针（对应于不同类型的变量）。这样做是为了节省存储空间，因为未初始化的全局变量和静态变量不需要额外的存储空间来保存初始值。

至于未初始化的全局变量和已初始化的全局变量，它们通常放置在全局/静态存储区的不同部分。具体地，未初始化的全局变量存储在BSS段，而已初始化的全局变量则存储在数据段（Data Segment）中。

4、内存对齐？为什么字节对齐？

内存对齐是指内存中数据存储的起始位置按照一定规则对齐到特定的地址上。在计算机系统中，数据的存储和访问通常是按照字节进行的，而不是按照单独的位。因此，为了提高数据的读取和写入效率，数据在内存中的存储位置通常需要满足一定的对齐要求，即数据的起始地址应该是特定值的倍数。

为什么需要字节对齐呢？

1. 硬件要求： 很多硬件平台要求数据按照特定的字节对齐方式进行访问，否则可能会导致访问异常或性能下降。例如，某些处理器要求整型数据的地址必须是4的倍数，双精度浮点数的地址必须是8的倍数。
2. 提高访问效率： 字节对齐可以减少内存访问次数，提高数据的读取和写入效率。如果数据没有按照要求对齐，可能需要多次内存访问才能读取或写入完整的数据，而按照要求对齐后，可以通过一次内存访问就能读取或写入完整的数据。
3. 优化缓存性能： 很多处理器具有缓存系统，缓存系统通常也按照字节对齐的方式工作。如果数据按照缓存行的大小对齐，可以提高缓存的命中率，减少缓存失效，进而提高程序的性能。

5、vector中push_back和emplace_back的区别？

1. push_back：
   • push_back接受一个参数，将该参数的副本添加到vector的末尾。
   • 当使用push_back添加元素时，会调用元素类型的拷贝构造函数来创建一个临时副本，然后将这个副本添加到vector中。这意味着如果元素类型有拷贝构造函数，会进行一次拷贝操作。
   • 适用于传统的类型，如基本类型和自定义类型，但对于构造函数参数较多或有性能要求的情况可能效率不高。
2. emplace_back：
   • emplace_back接受多个参数，直接在vector的末尾构造一个元素。
   • 当使用emplace_back添加元素时，会直接在vector的内存空间中就地构造一个元素，省去了拷贝构造函数的调用。这意味着可以避免额外的拷贝操作，提高了效率。
   • 适用于需要传递多个参数或有性能要求的情况，可以避免额外的拷贝操作。

6、C++中的多态？说一下虚函数的多态？

C++中，多态性是指对象可以根据当前的实际类型来调用不同的函数。

1. 虚函数：
   • 虚函数是在基类中声明为virtual的函数，它可以被子类继承并重写。
   • 虚函数的调用在运行时解析，而不是在编译时确定。这意味着通过基类指针或引用调用虚函数时，实际调用的是对象的实际类型所对应的函数。
   • 虚函数使得基类指针或引用可以指向子类对象，并且通过这些指针或引用调用虚函数时可以实现多态行为。
2. 实现原理：
   • 虚函数的实现通常借助于虚函数表（vtable）来实现。每个类（包括基类和子类）都有一个对应的虚函数表，表中存储了虚函数的地址。
   • 对象的内存布局中通常包含一个指向虚函数表的指针（vptr），这个指针在对象创建时被初始化为指向该类的虚函数表。
   • 当调用虚函数时，实际上是通过对象的vptr找到对应的虚函数表，然后根据函数在表中的位置来调用正确的函数。

给个例子：

class Base {
public:
    virtual void show() {
        cout << "Base class\n";
    }
};

class Derived : public Base {
public:
    void show() override {
        cout << "Derived class\n";
    }
};

int main() {
    Base* b;
    Derived d;
    b = &d;
    b->show();  // 调用的是Derived类中的show函数，实现了多态
    return 0;
}

7、内联函数？内联函数的缺点？

内联函数是在编译器处理时将函数调用处用函数体替换的一种函数。内联函数可以减少函数调用的开销，提高程序的执行效率。在C++中，可以通过在函数定义前加上inline关键字来声明内联函数，但实际是否内联取决于编译器。

内联函数的缺点：

1. 代码膨胀：内联函数会将函数体复制到每个调用点，如果函数体较大或者被频繁调用，会导致代码膨胀，增加可执行文件的大小。
2. 编译时间增加：由于内联函数会在每个调用点展开，编译器需要处理更多的代码，可能会增加编译时间。
3. 限制：内联函数不能包含复杂的控制结构（如循环和递归），因为编译器需要在编译时展开函数调用，这些结构会导致展开过程复杂化。
4. 可读性：过度使用内联函数会导致代码可读性降低，因为函数体的逻辑被分散到各个调用点。

8、tcp的可靠传输？拥塞控制？流量控制？

1. 可靠传输：TCP使用序号和确认机制来实现可靠传输。发送方将数据分割成合适大小的报文段，并为每个报文段编号，接收方收到报文段后发送确认，如果发送方在一定时间内未收到确认，将重新发送该报文段。这样可以保证数据的可靠传输。
2. 拥塞控制：拥塞控制是TCP避免网络拥塞的重要机制。TCP通过维护一个拥塞窗口（cwnd）来控制发送数据的速率。拥塞窗口的大小受到网络拥塞程度和网络负载的影响，通过动态调整拥塞窗口大小，TCP可以在不造成网络拥塞的情况下提高数据传输效率。
3. 流量控制：流量控制是为了防止发送方发送速度过快而导致接收方无法处理的情况。TCP使用滑动窗口机制来实现流量控制。接收方会告诉发送方自己的接收窗口大小，发送方根据接收窗口大小来控制发送速率，保证发送方发送的数据不会超过接收方处理能力。

9、IP数据报的报头字段？TTL的设置了解过吗？

IP数据报的报头字段包括：

1. 版本（Version）：指示IP协议的版本，通常为IPv4或IPv6。
2. 头部长度（Header Length）：指示IP头部的长度，以32位字（4字节）为单位。
3. 区分服务（Type of Service）：用于指定数据报的优先级和服务质量要求。
4. 总长度（Total Length）：指示整个IP数据报的长度，包括头部和数据部分，以字节为单位。
5. 标识（Identification）：用于标识发送端分片的原始数据报的唯一标识符。
6. 标志（Flags）：包含三个位，分别是禁止分片（DF）、更多分片（MF）和保留位。
7. 片偏移（Fragment Offset）：指示该片段在原始数据报中的位置。
8. 生存时间（Time to Live，TTL）：指定数据报在网络中可以传输的最大跳数。每经过一个路由器，TTL值减一，当TTL为0时，数据报会被丢弃。
9. 协议（Protocol）：指示数据报中的数据部分使用的协议，如TCP、UDP等。
10. 头部校验和（Header Checksum）：用于检测IP头部在传输过程中是否发生了错误。
11. 源地址（Source Address）：指示数据报的发送端IP地址。
12. 目标地址（Destination Address）：指示数据报的接收端IP地址。

TTL的设置是为了防止数据报在网络中无限循环，当数据报经过路由器时，路由器会将TTL减一，并且如果TTL减为0时，路由器会丢弃该数据报，并向发送端发送ICMP超时消息。通过设置TTL，可以确保数据报在网络中不会无限传输，避免网络中的拥塞和资源浪费。

10、怎么实现断点续传？

断点续传通常用于文件下载，以允许用户在下载过程中暂停并在稍后恢复下载，而无需重新下载整个文件。实现断点续传的关键是在客户端和服务器端之间维护下载的状态信息，以便在恢复下载时知道从哪里继续下载。

实现断点续传的一般步骤：

1. 客户端请求文件下载：客户端向服务器发送文件下载请求，并在请求中包含上次下载的终止点（即文件的字节偏移量）。
2. 服务器处理请求：服务器接收到下载请求后，根据客户端提供的终止点，从文件的对应位置开始读取文件，并将数据发送给客户端。
3. 客户端接收数据：客户端接收到服务器发送的数据，并将数据写入本地文件的对应位置。
4. 断开连接：下载过程中，客户端和服务器之间可能发生连接断开等情况，需要处理这些情况。当连接断开时，客户端需要记录当前已下载的位置，以便在恢复下载时使用。
5. 恢复下载：如果下载过程中发生断开，客户端需要重新连接服务器，并在请求中包含上次下载的终止点，以便服务器知道从哪里继续发送数据。服务器收到恢复下载的请求后，从上次终止点开始发送数据。

实现断点续传时，需要注意的是：

• 文件切片：可以将文件切分为多个小块进行下载，每个小块完成下载后，再合并为完整的文件。
• 断点续传记录：客户端需要记录已经下载的文件块和位置信息，以便在恢复下载时使用。
• 下载状态维护：服务器需要维护每个客户端的下载状态信息，以便在恢复下载时知道从哪里继续发送数据。
• 并发下载：可以使用多线程或多进程进行文件下载，加快下载速度。

11、算法题：最长回文子串

思路：

以字符串"babad"为例。

1. 初始化状态：
   • 首先创建一个二维数组 dp，其大小为 n x n（n 为字符串长度），并初始化所有元素为 false。
   • 对于长度为 1 的子串，即 dp[i][i]，将对应位置的元素设为 true，因为单个字符肯定是回文串。
2. 状态转移：
   • 接下来从长度为 2 的子串开始，逐步扩展到长度为 n 的子串，计算 dp[i][j] 的值。
   • 对于每个长度为 len 的子串，枚举起始位置 i，计算结束位置 j = i + len - 1。
   • 如果 s[i] == s[j] 且 dp[i+1][j-1] 为 true，则说明去掉头尾两个字符后的子串是回文串，即 dp[i][j] = true。
3. 记录最长回文子串：
   • 在状态转移的过程中，记录下最长的回文子串的起始位置和长度。
   • 每次更新 dp[i][j] 为 true 时，更新起始位置 start = i 和最大长度 maxLen = len。
4. 返回结果：
   • 最后根据记录的起始位置 start 和最大长度 maxLen，使用 substr 方法从原始字符串中取出最长回文子串并返回。

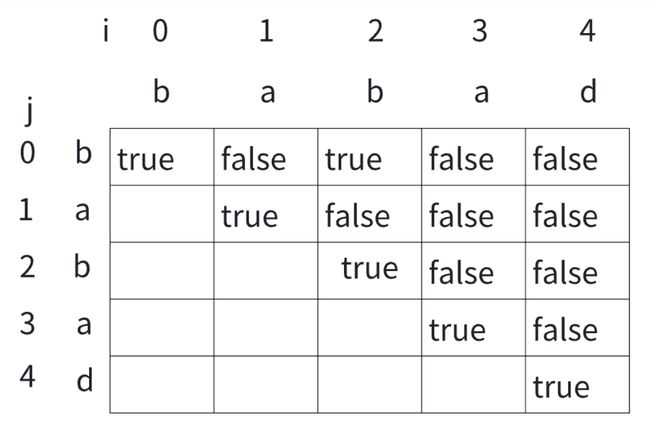
给个表格帮助大家理解：

表格中，对角线上的格子都表示长度为 1 的子串，因为单个字符肯定是回文串，所以都标记为 true。

然后我们开始计算长度为 2 的子串，例如 ba 和 ab，如果两个字符相同，则标记为 true，否则标记为 false。在这个例子中，ba 和 ab 都不是回文串，所以对应的格子都标记为 false。

接着我们计算长度为 3 的子串，例如 bab 和 aba，如果首尾两个字符相同并且去掉首尾字符的子串是回文串，则标记为 true，否则标记为 false。在这个例子中，bab 是回文串，所以对应的格子标记为 true，而 aba 也是回文串，所以对应的格子也标记为 true。

最后我们计算长度为 4 的子串，例如 baba，同样地，如果首尾两个字符相同并且去掉首尾字符的子串是回文串，则标记为 true，否则标记为 false。在这个例子中，baba 不是回文串，所以对应的格子标记为 false。

最终，我们可以根据这个表格得到最长的回文子串是 “bab”。

参考代码：

#include 
#include 
#include 
using namespace std;

string longestPalindrome(string s) {
    if (s.empty()) return "";
    int n = s.length();
    vector> dp(n, vector(n, false));  // 定义二维动态规划数组
    int start = 0, maxLen = 1;  // 记录最长回文子串的起始位置和长度
    for (int i = 0; i < n; ++i) {
        dp[i][i] = true;  // 单个字符肯定是回文串
        if (i < n - 1 && s[i] == s[i + 1]) {
            dp[i][i + 1] = true;  // 相邻字符相同则是回文串
            start = i;
            maxLen = 2;
        }
    }
    for (int len = 3; len <= n; ++len) {  // 枚举子串长度
        for (int i = 0; i + len - 1 < n; ++i) {  // 枚举子串起始位置
            int j = i + len - 1;  // 子串结束位置
            if (s[i] == s[j] && dp[i + 1][j - 1]) {
                dp[i][j] = true;  // 根据状态转移方程计算 dp[i][j]
                start = i;
                maxLen = len;
            }
        }
    }
    return s.substr(start, maxLen);  // 返回最长回文子串
}

int main() {
    string s = " ";
    std::cout << "输入字符串：";
    std::cin >> s;
    std::cout << longestPalindrome(s) << std::endl;  // 输出最长回文子串
    return 0;
}