《视觉SLAM-非线性优化与g2o-高翔》笔记

《视觉SLAM-非线性优化与g2o-高翔》笔记

本文是观看视频《视觉SLAM-非线性优化与g2o-高翔》整理的笔记。

1. 从滤波到优化

1.1 模型

状态变量$x$： $x=[x_1,x_2,...,x_N,y_1,y_2,...,y_M]$
运动模型$f$： $x_k=f(x_{k-1},u_k)+v_k$
观测模型$g$： $z_{k,j}=g(x_k,y_j)+n_{k,j}$
其中，$x_i$为位姿，$y_i$为路标坐标，都是未知量。$u$为运动输入量，$z$为观测值，都是测量值。

1.2 传统EKF方法

在工作点附近计算雅可比矩阵（一阶偏导）$F$ 和 $G$。
$$\begin{gathered} F=:\frac{\delta f}{\delta x_k}|{\hat{x}}_{k-1}{v}_k\sim N(0,Q_k) \\ G=:\frac{\delta g}{\delta x_k}|{\hat{x}}_k{n}_{k,j}\sim N(0,R_k) \end{gathered}$$

step1. 预测：估计先验的均值和协方差矩阵
$${\breve{x}}_k=f({\hat{x}}_{k-1},u_k){\breve{P}}_{k+1}=F_k{\hat{P}}_k{F}_k^T+Q_k$$

step2. 更新：计算卡尔曼增益，并用观测模型纠正先验模型，得到后验估计
$$\begin{gathered} K_k={\breve{P}}_k{G}_k^T(G_k{\breve{P}}_k{G}_k^T+R_k{)}^{-1} \\ {\hat{x}}_k={\breve{x}}_k+K_k(z-\hat{z}){\hat{P}}_k=(i-K{G}_k){\breve{P}}_k \end{gathered}$$

EKF的问题：
线性化误差，无迭代，噪声非高斯，需要维护一个大的协方差矩阵（平方级别复杂度）。
解决思路=>使用非线性优化

1.3 非线性优化思路

思路	问题
1. 设定目标函数，选定初值 状态向量：$x=[x_1,x_2,...,x_N,y_1,y_2,...,y_M]$	目标函数是什么？
2. 寻找梯度，使目标函数下降	梯度如何计算？
3. 梯度下降，迭代直到收敛	梯度只是局部下降，如何保证目标函数下降？

1.4 目标函数

在视觉和激光SLAM中，运动模型差别较小，观测模型则有所差异。这里我们以观测模型为例。
观测模型： $z_{k,j}=g(x_k,y_j)+n_{k,j}{n}_{k,j}\sim N(0,\Sigma )$
误差分布： $z_{k,j}\sim N(g(x_k,y_j),\Sigma )$

以Bayers方式理解，优化的目标是：在已知观测值$z$的条件下，求能使$P(x,y|z)$概率大最的$xy$。即求：

$$(x,y{)}^{\ast }=\underset{x,y}{\mathrm{argmax}}P(x,y|z)$$

根据贝叶斯方程，后验与似然×先验成正比。$P(x,y|z)\propto P(z|x,y)P(x,y)$
则有两种方式求解 $xy$：

• 最大似然（MLE）：$(x,y{)}^{\ast }=\underset{x,y}{\mathrm{argmax}}P(z|x,y)$
• 最大后验（MAP）：$(x,y{)}^{\ast }=\underset{x,y}{\mathrm{argmax}}P(z|x,y)P(x,y)$

一般不知道路标的先验位置，所以用MLE多一些。

怎么求MLE呢？
我们会使用负对数简化目标函数。

这么做是因为，高斯分布函数有如下性质：取负对数后，可以分为两部分，前一部分与$z$无关，求极值时可以不考虑；而后一部分的结构比变换之前简单了很多。

$$\begin{gathered} P(z)=-ln\{\frac{1}{{(2\pi )}^{N}det\Sigma }\exp [\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )]\} \\ =\frac{1}{2}ln[{(2\pi )}^{N}det\Sigma ]+\frac{1}{2}[(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )] \end{gathered}$$

对变量求极大值，相当于求负对数的极小值。则求下式即可达到最大似然：
$$\begin{array}{rl}\underset{x,y}{\mathrm{argmax}}P(z|x,y)& =\underset{x,y}{\mathrm{argmin}}-ln(P(z|x,y))\\ & =\underset{x,y}{\mathrm{argmin}}(z-\mu {)}^T{\Sigma }^{-1}(z-\mu )\end{array}$$

我们知道 $z_{k,j}\sim N(g(x_k,y_j),\Sigma )$，则有
$$\begin{array}{rl}\underset{x,y}{\mathrm{argmax}}P(z|x,y)& =\underset{x,y}{\mathrm{argmin}}[z-g(x,y){]}^T{\Sigma }^{-1}[z-g(x,y)]\\ & =\underset{x,y}{\mathrm{argmin}}(e^T\Sigma e)\end{array}$$

其中，${\Sigma }^{-1}$是信息矩阵，$\Sigma$是噪声分布的协方差矩阵。

考虑整个系统
误差来源有二：运动模型误差，和观测模型误差。假设都符合高斯分布：
$e_{v,k}=x_k-f(x_{k-1},v_k)=v_k\sim N(0,Q_k)$
$e_{y,k,j}=z_{k,j}-g(x_k,y_j)=n_{k,j}\sim N(0,R_k)$

将两种误差都考虑进来，则目标函数可以定义为：
$$T(x,y)=\sum _{k=1}^N{e}_{v,k}^T{\Sigma }_{v,k}^{-1}{e}_{v,k}+\sum _{k=1}^N\sum _{j=1}^M{e}_{y,k,j}^T{\Sigma }_{y,k,j}^{-1}{e}_{y,k,j}$$

其中，$N$为epoch个数，$M$为观测值个数。

若不考虑运动模型，就类似Bundle Adjustment只有观测，成为一个最小二乘问题。

1.5 计算梯度

将$xy$合并记为$x$，还是以观测误差为例： $e(x)=z-g(x)$。整体的误差项（目标函数）：
$$E(x)=e(x{)}^T{\Sigma }^{-1}e(x)$$

给$x$一个微小偏移量，新的误差为：
$$E(x+\Delta x)=e^T(x+\Delta x){\Sigma }^{-1}e(x+\Delta x)$$

用泰勒公式 $e(x+\Delta x)\approx e+J\Delta x$ 进行一阶线性展开（$e$，$J$都是在工作点$x$处计算的）：

$$\begin{array}{rl}E(x+\Delta x)& \approx (e+J\Delta x{)}^T{\Sigma }^{-1}(e+J\Delta x)\\ & =e^T{\Sigma }^{-1}e+2e^T{\Sigma }^{-1}J\Delta x+\Delta x^T{J}^T{\Sigma }^{-1}J\Delta x\\ & =E(x)+2e^T{\Sigma }^{-1}J\Delta x+\Delta x^T{J}^T{\Sigma }^{-1}J\Delta x\end{array}$$

则$E$的增量：
$$\begin{array}{rl}\Delta E& =E(x+\Delta x)-E(x)\\ & =2e^T{\Sigma }^{-1}J\Delta x+\Delta x^T{J}^T{\Sigma }^{-1}J\Delta x\end{array}$$

$\underset{x,y}{\mathrm{argmin}}(E)=\underset{x,y}{\mathrm{argmin}}(\Delta E)$ 。要使$\Delta E$尽可能的小，解$\delta \Delta E/\delta \Delta x=0$ 即可。
$$\begin{array}{rl}\frac{\delta \Delta E}{\delta \Delta x}& =(2e^T{\Sigma }^{-1}J{)}^T+2(J^T{\Sigma }^{-1}J)\Delta x\\ & =2J^T{\Sigma }^{-1}e+2J^T{\Sigma }^{-1}J\Delta x=0\end{array}$$

则得到以下形式的线性方程，可以解得$\Delta x$，该更新值可使目标函数 $E$ 减小。
$$\begin{array}{rl}{J}^T{\Sigma }^{-1}J\Delta x& =-J^T{\Sigma }^{-1}e\\ H\Delta x& =-b\end{array}$$

$H=:J^T{\Sigma }^{-1}J$，是Hessian矩阵的近似。$b=J^T{\Sigma }^{-1}e$。

问题：

• 雅可比矩阵 $J=\Delta e/\Delta x$ 怎么算？
• 怎么解$\Delta x$？
  • 当规模小的时候可以用$\Delta x=H^{-1}b$
  • 当方程规模大时呢？利用稀疏性。

1.6.1 雅可比矩阵 $J$ 怎么算

还是以相机观测模型$z=g(x,y)$为例：

如图，控制点的全局坐标 $y$，通过相机外参 $R$ 和 $t$ 转到相机坐标系，乘以相机内参$K$，再除以距离z，得到像点坐标$u,v$（这里没用齐次坐标，乘以$D$取前两个值）。 最后用李代$\xi$数表示相机的pose：

$$\begin{array}{rl}\left[\begin{array}{c}u\\ v\end{array}\right]& =\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right]\frac{1}{z_y}\left[\begin{array}{ccc}{f}_x& 0& 0\\ 0& f_y& 0\\ 0& 0& 1\end{array}\right](Ry+t)\\ z& =D\frac{1}{z_y}K(Ry+t)=\frac{1}{z_y}DK\exp ({\xi }^{\wedge })y:=g(\xi ,y)\end{array}$$

可以看到，误差方程 $e=z-g(\xi ,y)$ 包含两个自变量，相机位姿 $\xi$ 和控制点坐标 $y$。

a) 误差$e$关于pose $\xi$求导

e对于$\xi$的模型为：
$$\begin{array}{r}e(\xi )=z-g(x,y)=z-\frac{1}{z_y}DK\exp ({\xi }^{\wedge })y\end{array}$$

对pose加一个扰动（定义一个广义的加法，实际是乘法）：
$$\begin{array}{rl}e(\xi \oplus \delta \xi )& =z-\frac{1}{z_y}DK\exp [(\xi \oplus \delta \xi {)}^{\wedge }]y\\ & =z-\frac{1}{z_y}DK\exp (\delta {\xi }^{\wedge })\exp ({\xi }^{\wedge })y\\ & \approx z-\frac{1}{z_y}DK(1+\delta {\xi }^{\wedge })\exp ({\xi }^{\wedge })y利用指数的泰勒展开exp(x)\approx 1+x\\ & =z-\frac{1}{z_y}DK\exp ({\xi }^{\wedge })y-\frac{1}{z_y}DK\delta {\xi }^{\wedge }\exp ({\xi }^{\wedge })y\\ e(\xi \oplus \delta \xi )& =e(\xi )-\frac{1}{z_y}DK\delta {\xi }^{\wedge }\exp ({\xi }^{\wedge })y\end{array}$$

定义临时变量$Ty=[x,y,z]$，则有：（详见博客推导直接法）
$$\begin{array}{rl}{J}_{\xi }\delta \xi & =e(\xi \oplus \delta \xi )-e(\xi )=-\frac{1}{z_y}DK\delta {\xi }^{\wedge }\exp ({\xi }^{\wedge })y\\ J_{\xi }\delta \xi & =-\left[\begin{array}{ccc}\frac{f_x}{z}& 0& \frac{-f_{x}x}{z^2}\\ 0& \frac{f_y}{z}& \frac{-f_{y}y}{z^2}\end{array}\right]\left[\begin{array}{cc}I& -(Ty{)}^{\wedge }\end{array}\right]\delta \xi \end{array}$$

以上为观测模型对相机pose的求导。pose6维，像点2维，最后求出一个2×6的$J$矩阵。

b）误差$e$关于3D点求导

过程类似，最后得到一个2×3的矩阵：
$$\begin{gathered} e(y+\delta y)\approx e(y)+J_y\delta y \\ {J}_y=-\left[\begin{array}{ccc}\frac{f_x}{z}& 0& \frac{-f_{x}x}{z^2}\\ 0& \frac{f_y}{z}& \frac{-f_{y}y}{z^2}\end{array}\right]R \end{gathered}$$

c）小结

对于针孔相机的观测模型 $z=g(x,y)$，相机pose和空间点有微小运动时，像素的变化为：
$$e(x+\Delta x,y+\Delta y)\approx e(x,y)+J_{\xi }\delta \xi +J_y\delta y$$

有耐心的话，还可以推导二阶Taylor展开式。

非线性优化SLAM：考虑所有变量和边，求解整个问题。

1. 把所有相机pose和空间点放在一个state vec里面：
   $x=[x_1,x_2,...,x_N{,}_1,x_2,...,x_M{]}^T$
2. 相机对每个控制点的观测误差： $e_g=z-g(x)$，
   每次运动的运动误差： $e_f=x-f(x)$，
   将所有误差的二次型 $E=e^T\Sigma e$ 相加，
   得到目标函数 $T(x,y)=\Sigma E_f+\Sigma E_g$。
3. 求 $\underset{x}{\mathrm{argmax}}P(x|u,z)=\underset{x}{\mathrm{argmin}}(T)$，需要解 $H\delta x=-b$。
   $H=\sum (J^T{\Sigma }^{-1}J)$
   $b=\sum (-J^T{\Sigma }^{-1}e)$
4. 更新一次 $x^{\ast }=x\oplus \delta x$。（这里是广义的加号，pose不能直接相加）
   以上是Gauss-Newton迭代法。

那么其他的迭代方法呢？

2 梯度下降法

给定目标函数$f(x)$，当前点$x_{OP}$，梯度$\Delta x$，如何下降？

• 1 最速下降法
  • 找寻最优步长$\lambda =\arg {\min }_{\lambda >0}f(x+\lambda x)$，下降慢
  • $x=x_{OP}+\lambda \Delta x$
• 2 牛顿法 Newton
  • 在工作点附近，求一阶+二阶导数（二阶导Hessian难算），可能不正定
    $\begin{array}{rl}f(x_{OP}+\delta x)& \approx f(x_{OP})+\frac{\delta f}{\delta x}{|}_{x_{OP}}\delta x+\frac{1}{2}\delta x^T\frac{{\delta }^{2}f}{\delta x\delta x^T}{|}_{x_{OP}}\delta x\\ & =f(x_{OP})+Jacobian\delta x+\frac{1}{2}\delta x^{T}Hessian\delta x\end{array}$
  • $H\delta x^{\ast }=-J^{T}e$
• 3 高斯牛顿法 G-N
  • 用$J^{T}J$近似Hessian矩阵，可能半正定导致$J^{T}J$不可逆
  • $J^{T}J\delta x^{\ast }=-J^{T}e$
• 4 Leverberg-Marquardt法
  • 引入拉格朗日乘子，在一个小的邻域范围（trusted region）中求$mi{n}_{x}f(x)+\lambda ||x|{|}^2$
  • G-N失效，目标函数不下降时，增大$\lambda$近似最速法；反之减小$\lambda$近似G-N法
  • $(J^{T}J+\lambda I)\delta x^{\ast }=-J^{T}e$

** 234都是二阶的方法，变量维度较高时，下降速度快。
** 非正定：当二次曲线开口向下，此时H不可逆，G-N法的$J^{T}J$是半正定的（$x^T{J}^{T}Jx=(Jx{)}^2>0$），但也可能无法求逆

• 5 Dogleg法
  • 在trusted region内部，用G-N
  • 否则用最速，但最速的下降方向可能在region内/外部
    • 在内部，使用两个梯度的混合
    • 在外部，则缩小到region边界

小结

• 最速下降：计算快，收敛慢，有zig-zag现象
• Newton：收敛慢，Hessian复杂
• G-N：$J^{T}J\approx H$计算方便，可能失效
• L-M：$J^{T}J+\lambda I$控制$\lambda$调整收敛结果
• DogLeg：G-N与最速的混合

后三个常用，G-N最常用。

对于所有优化的问题：

• 初值敏感
• 局部可能极小

SLAM目前是个非凸问题：

• 解不唯一
• 依赖初值（前端需要提供好的匹配和初值）

3 图优化与稀疏性

一个非线性的优化问题，可以表示成图：$G=V,E$

• V- 节点：优化变量（pose，point）
• E- 边：误差项（运动方程，观测方程）

凸优化的关键问题：当图的规模较大时（几千到几万个变量），如何求解？
$$H\delta x^{\ast }=-b$$
小规模可求逆：$\delta x^{\ast }=-H^{-1}b$。但求逆的复杂度为$O(N^3)$。
N很大的时候怎么办？利用稀疏性。

3.1 稀疏性

只有观测方程时
优化变量：$x_k=[x_1,x_2,...,x_N,x_1,x_2,...,x_M{]}_k$
某个约束：$e_{jk}=z_{jk}-g(x_i,y_k)$

该约束关于自变量的雅可比只有两个地方非0（如下图左）。而组成的H矩阵也只有四个地方非零（如下图右）。也就是说$H\delta x=-b$的$H$是稀疏的。
$$\begin{array}{rl}\frac{d{e}_{jk}}{dx}& =[0,0,...,\frac{d{e}_{jk}}{d{x}_j},...,\frac{d{e}_{jk}}{d{y}_k},...{]}^T\\ H_{jk}& =J_{jk}^T{\Sigma }_{jk}^{-1}{J}_{jk}\end{array}$$

而组成的H矩阵也只有四个地方非零，如上图右。也就是说$H\delta x=-b$的$H$是稀疏的。
$$H_{jk}=J_{jk}^T{\Sigma }_{jk}^{-1}{J}_{jk}$$

j=[1:N] 为pose个数，k=[1:M]为空间点个数。如果每个约束只有一个pose和一个point，当每个pose可以看到所有point时，矩阵形如下图：

$$\left[\begin{array}{cc}{H}_{11}& H_{12}\\ H_{12}^T& H_{22}\end{array}\right]\left[\begin{array}{c}\delta x_1^{\ast }\\ \delta x_2^{\ast }\end{array}\right]=\left[\begin{array}{c}-b_1\\ -b_2\end{array}\right]$$

$\delta x_1$为pose部分，$\delta x_2$为point部分，一般jpose数远小于point数，形成一个箭头形的稀疏矩阵。

3.2 加速方式

a) 稀疏Schur Complement（类似消元法）

1. 对上面的方程左乘$\left[\begin{array}{cc}I& -H_{12}{H}_{22}^{-1}\\ 0& I\end{array}\right]$得到：

$$\left[\begin{array}{cc}{H}_{11}-H_{12}{H}_{22}^{-1}{H}_{12}^T& 0\\ H_{12}^T& H_{22}\end{array}\right]\left[\begin{array}{c}\delta x_1^{\ast }\\ \delta x_2^{\ast }\end{array}\right]=\left[\begin{array}{c}-b_1+H_{12}{H}_{22}^{-1}{b}_2\\ -b_2\end{array}\right]$$

2. 解 $(H_{11}-H_{12}{H}_{22}^{-1}{H}_{12}^T)\delta x_1^{\ast }=-b_1+H_{12}{H}_{22}^{-1}{b}_2$ 得到 $\delta x_1^{\ast }$（$H_{22}^{-1}$对角易求，pose少求逆容易）
3. 解 $H_{12}^T\delta x_1^{\ast }+H_{22}\delta x_2^{\ast }=-b_2$ 得到 $\delta x_2^{\ast }$（$H_{22}^{-1}$对角易解）

复杂度从$O(N+M{)}^3$ => $O(N^3+M^3)$。
当M>>N时，加速明显。
整个过程不需要求解$H^{-1}$。

b) 稀疏Cholesky

Cholesky分解解方程
原始方程：$Ax=b$
分解 $A$：$A=U{U}^T$。并设中间变量 $y=U^{T}x$。则有：
$$Ax=U{U}^{T}x=Uy=b$$

求解时，先解$Uy=b$，再解$U^{T}x=y$ ，最终得到$x$。
$U$是个上三角矩阵，最底下那一行只有一个变量，因此逐行求解，就很快。

Cholesky解稀疏矩阵
原始方程：$H\delta x^{\ast }=-b$
分块并分解$H$为：
$$\left[\begin{array}{cc}{H}_{11}& H_{12}\\ H_{12}^T& H_{22}\end{array}\right]=\left[\begin{array}{cc}{U}_{11}& U_{12}\\ 0& U_{22}\end{array}\right]\left[\begin{array}{cc}{U}_{11}^T& 0\\ U_{12}^T& U_{22}^T\end{array}\right]$$

则可以计算U矩阵：
$H_{22}=U_{22}{U}_{22}^T$ =》$H_{22}$为对角块矩阵，易解$U_{22}$
$H_{12}=U_{12}{U}_{22}^T$ =》$U_{22}$已知且为对角块，易解$U_{12}$
$H_{11}=U_{11}{U}_{11}^T+U_{12}{U}_{12}^T$ =》$H_{11}$规模小，易解

那么可得：
$$H^{-1}=\left[\begin{array}{cc}{U}_{11}{U}_{11}^{-1}& -U_{11}^{-T}{U}_{11}^{-1}{U}_{12}{U}_{22}^{-1}\\ -U_{22}^{-T}{U}_{12}^T{U}_{11}^{-T}{U}_{11}^{-1}& U_{22}^{-T}(U_{12}^T{U}_{11}^{-T}{U}_{11}^{-1}{U}_{12}+I)U_{22}^{-1}\end{array}\right]$$

当有运动方程时

$H_{11}$不再是对角块，但稀疏性还在，还是可以求解。

3.3 小结

后端需要做的任务：

• 定义顶点和边，每条边对应一个误差项
• 求每个误差项，求其相对于优化变量的雅可比
• 所有误差放到一起，构建增量方程
• 求解增量方程
• 更新优化变量的估计值

4 G2O

4.1 简介

General graphic Optimization 通用图优化

g2o库提供的功能	用户要做的
多种类型图节点与边	构建、维护图模型
数值雅可比	（可选）提供解析雅可比
增量方程构建&求解	选择求解器与下降方法
多种下降方法(G-M, L-M)	执行优化
可视化工具	（可选）调用
	可选（自定义边，主动控制优化过程）

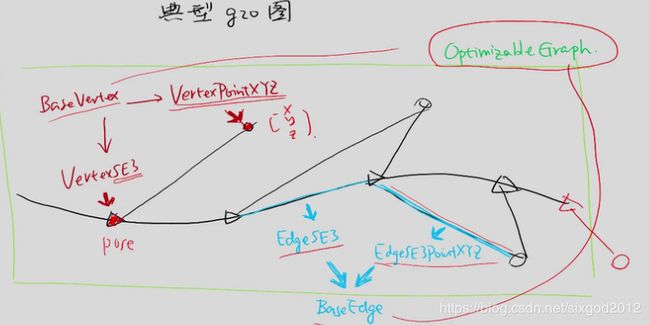
顶点：
位姿可以选VertexSE3（单目Sim3，激光SE2）
空间点可以选VertexPointXYZ
都基于基类BaseVertex

边：
pose-pose：EdgeSE3
pose-point：EdgeSE3PointXYZ
都基于基类BaseEdge

G2O的核心是一个Optimizable Graph

• Vertex可以选择fix固定住它的值，比如第一个点
• 存在多元边，如$e=z-g(x_1,x_2,y_1)$
• 多种优化算法
• 解$H\delta x=-b$时调用外部的库，稀疏问题可以选择一个稀疏库

4.2 使用

参考：深入理解图优化与g2o：g2o篇
大致步骤：

1. 初始化

// 先构造求解器（也就是我们要维护的图）
g2o::SparseOptimizer    optimizer;
// 使用Cholmod中的线性方程求解器（H dx = -b的求解器）
g2o::BlockSolver_6_3::LinearSolverType* linearSolver = new g2o::LinearSolverCholmod ();
// 6*3 的参数（单个误差项对应参数块）
 g2o::BlockSolver_6_3* block_solver = new g2o::BlockSolver_6_3( linearSolver );
// L-M 下降 （定义下降方式）
g2o::OptimizationAlgorithmLevenberg* algorithm = new g2o::OptimizationAlgorithmLevenberg( block_solver );

optimizer.setAlgorithm( algorithm );
optimizer.setVerbose( false );

2. 添加顶点和边
   optimier.addVertex
optimier.addEdge

3. 开始优化
   optimizer.optimize()

4. 读取优化结果

o[0] is undefined

* 核函数

普通误差项 $E=e^T{\Sigma }^{-1}e$是个二范数，随e的增长很快。
但当图中有一条错误的边，它的误差会很大，优化算法会费很大力气优化错误的边。
考虑到这点，想要使误差的增长不要那么快，引入核函数。

带核函数的误差项形式为：$E=\rho (\sqrt{e^T{\Sigma }^{-1}e})$
对普通的二范数，相当于$\rho (x)=x^2$

Huber核：
$$\rho (x)\{\begin{array}{l}{x}^2,|x|<b\\ 2b|x|-b^2,|x|\ge b\end{array}$$
大于边界b时变为线性增长。

* Pose Graph

只有pose没有point的图，在不关心point时可以使用，计算量小，侧重定位。
Pose Graph约束
对pose$x_k$和$x_l$测得[未完。。。]

5 小结

1. SLAM问题可以用非线性优化求解（高斯分布下对应最小二乘）
2. 我们关心：优化的目标函数，误差项，梯度，下降方式
3. 优化问题可以抽象成图模型
4. 图优化可以用g2o求解