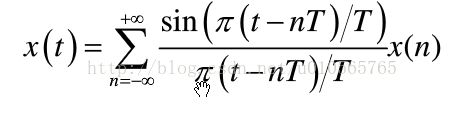信号采样点总结
采样率转换:
1)将一个信号从一个给定的采样率到另一个不同的采样率的过程称为采样率转换。
2)内插:内插往往就是线性(或直线)近似,这样就会形成一种误差,称为内插误差。将采样率减小某整数倍的过程是抽取,将采样率增加的一个整倍数因子的过程是内插。
3)抽取:将高采样率的信号减采样到一个低采样率的信号,
4)内插:首先用一种称之为增采样的运算在非零样本之间补若干灵芝样本产生一个高采样率Fy的中间信号;之后,将这个中间信号滤波以便将插入的零值样本填入,产生已聂插的高采样率信号。
5)过渡带的大小,决定了滤波器的阶次;过渡带越大,滤波器的阶次越低,过渡带的越小,滤波器的阶次越高。
1,一个信号是带限的(即它的傅里叶变换在某一有限的频带范围以外是0),并且它的样本取得足够密(相对于信号中的最高频率而言),那么这些样本值就能唯一的表示这一信号,并将原来的信号恢复出来,这一结果就是采样定理。
2,在采样定理中,采样频率必须大于2倍的最大截止频率,这个两倍的截止频率一般称为奈奎斯特率。
3,使用内插由样本重建信号:内插(就是用一个连续的信号对一组样本值的拟合,)是一个由样本值来重建某一函数的常用过程,这一重建过程结果既可以是近似的,也可以是完全准确的。一种简单有用的内插形式是:线性内插,就是将相邻的样本点用直线连接起来。
4,利用理想低通滤波器的单位冲激响应的内插通常称为带限内插。这种内插,只要x(t)是带限的,而采样频率又满足采样定理中的条件,就实现了信号的真正重建。
5,欠采样的效果:混叠现象;当采样频率小于最大截止频率两倍的时候就会发生信号重叠,这一现象叫做混叠。
6,将原来的信号提取每第N个点上的样本的过程称为抽取。抽取的效果就是将原来的序列扩展到一个较宽的频带部分。如果这个原始序列经由连续时间信号采样得到的,那么抽取的过程就可以看成在连续时间信号上将采样率减小为原来的1/N的结果。
7,序列可以被抽取而又不引入混叠,那么原来的连续时间信号是被过采样了的,从而原采样率可以减小而不会发生混叠。因此,抽取的过程往往称为减采样。
8,将一个序列转换到一个较高的等效采样率上,这种称为增采样或者内插。增采样的过程基本上就是一抽取或者减采样的逆过程。
9,传统的完成信号抽样率的转换有两种方法:模拟方法和数字方法。
10,重采样系统的基本模块是:抽取器和内插器,抽取可能产生混叠,内插产生镜像。在抽取前进行抗混叠滤波,在内插后进行抗镜像滤波。
11,只有在抽取之后的抽样率仍然满足抽样定理的要求时才能恢复出原始的信号,符合就回产生混叠,难以恢复原始信号。
12,线性插值法都是所谓的“”重采样滤波器“”
12.1:最近邻点插值:最近邻肌电插值又称为零阶插值;双线性插值:又称为一阶插值,先对水平方向进行一阶线性插值,然后再对垂直方向进行一阶线性插值。;双三次插值:又称三次卷积插值,是一种更加复杂的插值方式,即不仅考虑到四个直接林甸的灰度值的影响,还考虑到各邻点间灰度值变化率的影响。
二,实现信号重采样的方法有:基于线性插值的重采样,基于朗格朗日的重采样以及基于正弦插值的重采样。
1,线性插值:基于插值点相邻两点的幅值来线性的计算插值点的具体幅值;拉格朗日插值是利用拉格朗日插值多项式通过设置好长度的窗口来计算插值点的具体幅值;正弦插值是用三角多项式通过预先设置好长度的窗口来求得插值点的幅值。
2,多抽样率信号初六的优势:降低计算的复杂度,降低传输速率,减小存储零等;
3,线性重采样:思想是:用一条通过两个固定点的直线去逼近所有采样的这个点,,这意味着所要求的点和已经存在的两个点,这三个点位于同一条直线上。
3.1:线性重采样的基本思想是:1)将原始的采光率L,转换到新的采样率M,原始的信号的长度是N,求出新采光率下的信号的长度是:K= (M/L)*N;,就是在采样率为L的时候需要多少个点,在采样率为M的时候需要多少个点。
2)对每个离散的时间值:k(1<=k<=K),让实值nk的置为nk = (L/M)*k;nk为在原始采样间隔的情况下,要进行插值的具体位置。L为原始新品信号的采样频率,M为需要的新的采样频率,其中的L/M是频率的缩放因子。nk必须存在一个时间指数n(1<=n<=N)而且nk和n的关系必须满足:n<=nk<=n+1;
3)利用上面求得的nk求两个权值, w1 = nk-n; w2 = 1-w1;
4)将w1,w2,两个重采样权值与要插入到 点的相邻的两点的赋值线性结合,求得将要插入点的具体的幅值,y(k) = w1*x(n+1) +w2*x(n);.使得添加的点和原来的采样点之间满足线性关系。
5)但是线性重采样有上采样和下采样两种情况,上采样会产生镜像,下采样会产生混叠,为了消除镜像和混叠,就需要将信号通过低通滤波器。为了解决不同采样率时遇到的不同情况,低通滤波器的位置将不同。上采样,在频域产生镜像,将新采样的频率下生成的音频信号通过低通滤波器,就会消除上采样产生的镜像;下采样,在频域产生混叠,就要在原始信号进行采样率转换之前进行低通滤波,避免产生混叠。
三,拉格朗日重采样:
1,设计思想是:用多项式去逼近原始音频信号并且在拉格朗日内插多项式的基础上计算重采样值。
2,步骤1,将音频信号的原始采样率L,转换到新的采样率M,原始信号的长度为N,新采样率下的音频信号长度是K;
3,对于你每个离散时间值:k(1<=k<=K),计算nk的值nk = (L/M)*k;nk为在原始采样间隔的情况下,要进行差值的具体位置,L为原始音频信号的原始采样率,这里和线性插值第2步一样
4,设置一个窗口长度,窗口长度决定用多少个点的幅值进行计算,以确定将要插值点的幅值,假设拉个朗日内插多项式的最高阶数是2*W,那么窗函数的大小就是2*w+1,这2*w+1个原始采样值的时间因子:n-w,,....,n-1,n,n+1,n+2,....,n+w;窗口的长度选择越长,计算的复杂度就越高,,所有重采样点的幅值就会越精确,但同时在时间开销放慢,选择的窗口长度约长,时间的开销量也随时增大。
5,对在该窗口长度内的点利用拉格朗日重采样权值公式计算,确定每个进行估值点的重采样权值qi的值,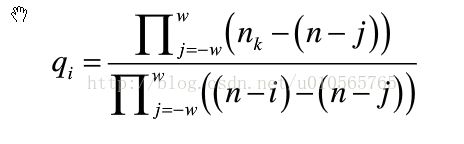
·6,将每个点的重采样权值qi和每点的赋值结合,求得插值点的具体幅值,y(k)的值便为带权值的2*w+1个原始样值的多项式按下式计算得到的:
7,采用拉格朗日的效果:选择较大的窗口长度不仅可以更精确的得到 插值点的赋值,还可以有效的消除镜像。为了更好地消除采样产生的混叠和镜像,就需要在适当位置进行低通滤波。上采样时,在采样后进行滤波,消除镜像;下采样时,在采样之前进行滤波,消除混叠现象。
三,正弦重采样
0,实施的原理;通过香农定理:将一个连续的音频信号x(t)可以经由离散值x(n)通过下式的公式重构:
依据香农理论,利用三角函数多项式--正弦多项式取逼近原始连续音频信号并且在正弦内插多项式的基础上计算重采样的样值。
1,将音频信号的原始采样率L,转换到新的采样率M,原始信号的长度为N,新采样率下的音频信号长度是K;
2,对每个离散的时间值:k(1<=k<=K),让实值nk的置为nk = (L/M)*k;nk为在原始采样间隔的情况下,要进行插值的具体位置。L为原始新品信号的采样频率,M为需要的新的采样频率,其中的L/M是频率的缩放因子。nk必须存在一个时间指数n(1<=n<=N)而且nk和n的关系必须满足:n<=nk<=n+1;
3,设置一个窗口的长度,窗口的长度决定用多少个点的幅值进行计算来确定将要插值点的幅值。假设正弦内插多项式的最高的阶数是2*w,那么窗函数的大小就是2*w+1,这2*w+1原始样值的时间因子![]() ;同拉格朗日重采样一样,窗口的长度的选择的越长,计算的复杂度就越高,所要重采样点的赋值就会越精确,但是在时间开销方面,窗口长度越长,时间开销就会越大。
;同拉格朗日重采样一样,窗口的长度的选择的越长,计算的复杂度就越高,所要重采样点的赋值就会越精确,但是在时间开销方面,窗口长度越长,时间开销就会越大。
4,对在该窗口长度内的点利用正弦插值权值公式: 进行计算,确定每个进行估值点的重采样权值pi的值。
进行计算,确定每个进行估值点的重采样权值pi的值。
5,将每点的重采样权值pi和幅值进行结合,求得插值点的具体幅值,y(k)的值变为带权值的2*w+1个原始样值的多项式计算得到:
6,设计思想上和拉格朗日的设计思想类似,同样会遇到上采样和下采样两种情况;实验结果(建议自己试试)在采用正弦重采样进行转换的时候,选取较大的窗口长度消除镜像的效果没有拉格朗日重采样效果好。上采样后,经过低通滤波器消除镜像,下采样之前经过低通滤波器消除混叠。在时间上正弦要比拉格朗日时间花费少。
四,结果现象
1,线性插值适合下采样,拉格朗日适合在上采样时获得较好的结果。正弦重采样更加适合于上采样。
2,下采样是是产生的混叠现象:线性产生的混叠现象不是很明显,正弦和拉格朗日没有比正弦有明显的改善。但是在时间上,线性重采样有明显的的优势。所以在下采样是,是考虑使用下采样;;在上采样时,正弦重采样和拉格朗日重采样算法自身就可以很好的抑制镜像的产生,重采样得到的效果较好了,但是线性重采样在没有滤波器的时候,会发生严重的频率混叠现象。所以上采样时使用正弦或者拉格朗日。正弦和拉格朗日比较:在窗口较大的时候,正弦消除镜像的效果没有拉格朗日好;但是时间上占有优势。(对于窗口长度不用取很长的时候,估计两种效果,正弦略微好一些)
3,在收敛性上:为了提高拉格朗日重采样的精度,常常增加节点的个数,即提高拉格朗日重采样多项式的阶次。但是阶次过高会产生龙格现象:就是在有的情况下,并非取节点越多,多项式就越精确。正弦重采样实际谁给你是三角多项式插值“即许复杂的波形可以分解为一系列谐波的叠加,所以正弦重采样当窗口长度过大时,也会出现龙格现象。这是多有基于多项式差值的缺点。线性重采样是线性差值,只是用相邻两点来估计插入点的幅值,所以不会出现龙格现象。
4,拉格朗日比线性重采样:可更加精确的确定采样点的幅度值,而且能够根据需要在时间开销和重采样质量之间做出选择。
5,正弦重采样和拉格朗日重重采样均可以灵活的选取窗长,以适应不同的重采样的质量要求。窗长越长,重采样点的赋值就会越精确,但是窗长到一定的长度的时候,盖上的效果就会不太明显。同时,时间上,窗长越大,时间开销越大。可以在瞬变值很小或者较大时可以获得较好的效果。
6,通过信噪比,拉格朗日和正弦重采样的信噪比比线性重采样的信噪比大,但是这两者的窗口的宽度不能持续变大,一个是会出现龙格现象。一个是信噪比也不会有更好了。
从信噪比上看:上采样时:拉格朗日重采样和正弦重采样的信噪比区别都不大,但考虑时间开销,正弦重采样要比拉格朗日算法有优势。
7,从段信噪比上看:拉格朗日和正弦比线性在上采样和下采样时的段信噪比都好;在质量要求不严格的时候,可以使用线性重采样,实时性好;在相同的窗口宽度时,正弦比拉格朗日的在段信噪比方面相差无几,但是实时性正弦比拉格朗日要好。
8,下采样:线性重采样的算法不仅在时间上有优势,而且又较高的信噪比和段信噪比;上采样:正弦和拉格朗日均有较高的段信噪比,二者可以灵活的调节窗口的长度,在质量和时间上,相对于线性重采样是一种改进,正弦比拉格朗日稍微节省时间。