关于位运算以及实现四则运算的实现

1、>>（右移） ：将操作数向右 移动，高位补0

eg:int a = 6 的二进制是00000110
		a >> 2的结果就是00000001

2、<<（左移） ：将操作数向左移动，低位补0

eg:int a = 6的二进制是00000110
		a << 2的结果就是00011000

3、&（位与） :两个操作数a和b同时为1的时候结果为1，否则结果为0。

 eg:int a = 6的二进制是00000110，
	  int b = 3的二进制是00000011，
	  所以结果就是 a&b = 00000010。

4、|（位或）：两个操作数a和b只要有一个为1的时候结果就为1，否则结果为0。

	eg :int a = 6的二进制是00000110，
	  int b = 3的二进制是00000011，
	  所以结果就是 a|b = 00000111。

5、~（位非） :单个操作数a位取反，当前值为1结果则为0，当前值为0则结果为1。

eg:int a = 6的二进制是00000110
			a~ 的结果为11111001。

6、^（异或）：两个操作数a和b相同的时候结果为0，否则结果则为1。

eg: int a = 6的二进制是00000110，
	  int b = 3的二进制是00000011，
	  所以结果就是 a^b = 00000101。

使用位运算来实现int类型的加法操作

/**
* 位运算实现加法
*/
public int add(int a,int b){
		int index = 1;
		long beginTime = System.nanoTime();
		System.out.println(a+"+"+b+"位运算开始");
		int s1 = a^b;
		int s2 = (a&b)<<1;
		System.out.println("第"+index+"轮运算结果："+"s1当前值为:" +s1+" , "+"s2当前值为:" +s2);
		while(s2 != 0){
			index++;
			int temp1 = s1^s2;
			int temp2 = (s1&s2)<<1;
			s1 = temp1;
			s2 = temp2;
			System.out.println("第"+index+"轮运算结果："+"s1当前值为:" +s1+" , "+"s2当前值为:" +s2);
		}
		long endTime=System.nanoTime();
		System.out.println(a+"+"+b+"位运算结束！结果为"+s1+"，耗时："+(endTime-beginTime)/1000+"微秒");
		return s1;
	}

使用位运算来实现int类型的减法操作

/**
     * 减法
     * @param a
     * @param b
     * @return
     */
    public static int sub(int a,int b){
        b = ~b+1;
        int s1 =  a^b;
        int s2 = (a&b)<<1;
        int temp1 = s1;
        int temp2 = s2;
        while (temp2 != 0) {
            temp1 = s1^s2;
            temp2 = (s1&s2)<<1;
            s1 = temp1;
            s2= temp2;
        }
        return s1;

    }

使用位运算来实现int类型的乘法操作
使用加法来实现乘法：首先得到乘数b的每一位，依次将每一位的向左n位，最终相加得到结果，最后在判断符号是正数还是负数。

/**
     * 乘法
     * @param a
     * @param b
     * @return
     */
    public static int multip(int a,int b){
        int m1= a<0?(~a)+1:a;
        int m2=b<0?(~b)+1:b;
        int s1= 0;
        int num =0;
        int s2= (m2&(1<>num) != 0) {
            if (s2!=0) {
                s1 = add(s1,m1<

如果被除数比除数大太多的话，这样效率就不高，采用折半查找法先找到除数b的最大倍数，一直到倍数为0，最后将所有的倍数加起来就是商，剩下的被除数就是商。下面做的优化代码

/**
     * 折半法位运算除法
     * @param a
     * @param b
     * @return
     */
    public static int div1(int a,int b){
        int d1 = a<0?(~a)+1:a;
        int d2= b<0?(~b)+1:b;
        Assert.isTrue(b!=0,"除数不能为0");
        int num = 0;
        int i =31;
        while(i>=0){
            if (d2 <= (d1>>i)) {
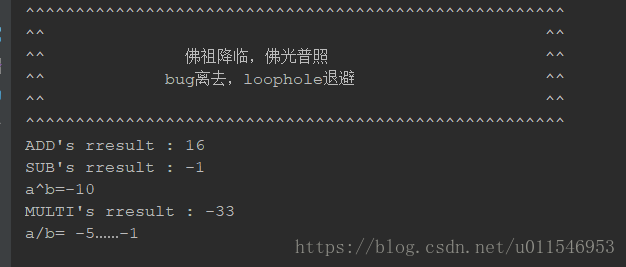
                num = num+(1<

简单的测试下，如下图

public static void main(String []args){
        consecration();
       int add = add(11,5);
       System.out.println("ADD's rresult : "+add);
       int sub = sub(11,12);
       System.out.println("SUB's rresult : "+sub);
       int multi = multip(11,-3);
       System.out.println("MULTI's rresult : "+multi);
       div1(11,-2);
    }

over