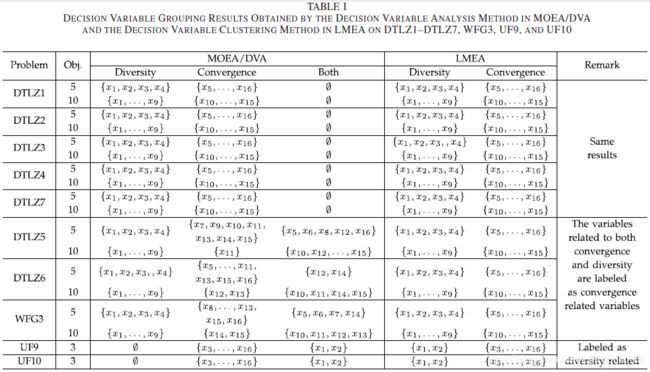
论文研读-基于决策变量聚类的大规模多目标优化进化算法

论文研读-基于决策变量聚类的大规模多目标优化进化算法

A Decision Variable Clustering-Based Evolutionary Algorithm for Large-Scale Many-Objective Optimization

觉得有用的话,欢迎一起讨论相互学习~

• 此篇文章为 X. Zhang, Y. Tian, R. Cheng and Y. Jin, "A Decision Variable Clustering-Based Evolutionary Algorithm for Large-Scale Many-Objective Optimization," in IEEE Transactions on Evolutionary Computation, vol. 22, no. 1, pp. 97-112, Feb. 2018, doi: 10.1109/TEVC.2016.2600642. 的论文学习笔记，只供学习使用，不作商业用途，侵权删除。并且本人学术功底有限如果有思路不正确的地方欢迎批评指正！

• 在本文中主要提出了两个创新点

1. 基于聚类(夹角)的决策变量分类方法
2. T-ENS 基于树的快速非支配算法
   本篇博客重点关注于 第一个创新点–即基于聚类(夹角)的决策变量分类方法
   对于 创新点2请参考原文与参考文献[54]X. Zhang, Y. Tian, R. Cheng, and Y. Jin, “An efficient approach to nondominated sorting for evolutionary multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 19, no. 2, pp. 201–213, Apr. 2015.

Abstract

• 现有的多目标优化的文献大多数关注目标的规模而很少有文献关注决策变量的规模，然而现实中很多问题不仅是超多目标的并且决策变量规模也很大。
• 为了解决这种大规模超多目标问题（MaOPs），提出了基于决策变量聚类的算法。
• 首先，决策变量会分成两类：1.收敛相关, 2. 多样相关 ，并且分别对这两种不同的变量使用不同的进化方式。
• 另外，提出了一种基于树结构的快速非支配排序方式以提高计算效率
• 最后，为了证明算法的效果，在具有10个目标5000个变量的算例上进行了实验，实验结果表明提出的算法相对于目前最先进的算法有显著的提升。

关键词

• 聚类，进化多目标优化，大规模优化，超多目标优化，非支配排序，树

Introduction

• 多目标优化问题（MaOP）是指涉及三个以上同时要优化的冲突目标的问题，这些问题广泛存在于实际应用中，例如工程设计[1]，空中交通管制[2]，地下水监测 [3]和分子设计[4]。 一般而言，MaOPs不能通过大多数旨在解决通常只涉及2-3个目标[5]-[9]的传统多目标优化问题（MOP）的多目标进化算法（MOEA）来解决。这主要是因为两个问题， 第一个问题是 收敛压力 的损失，这主要是由称为“主支配阻力”的现象引起的[1]。 这是由于以下事实：在超多目标优化中，大多数候选解决方案变得相互之间非支配，从而导致传统MOEA中基于支配的选择策略失效。另外有一个原因是 多样性管理。 在超多目标优化中，候选解会稀疏的分布在高维目标空间这会使得传统的多样性管理方法失效。为了解决上述的两种问题，已经提出了一些方法[10],[11].具体可以分为以下四类：

1. 提升算法收敛性能

• 为了提升算法的收敛压力，最直接的想法是直接修改传统帕累托支配的定义，这类方法主要有ε-dominance [12], [13], L-optimality [14], fuzzy dominance [15],preference order ranking [16], and θ-dominance [17].另一种想法是将一个额外的收敛性的指标结合到传统的支配方式中，这其中就包括the substitute distance assignment based NSGA-II 18, grid-based evolutionary algorithm [19], preference-inspired coevolutionary algorithm(表现启发的协同进化算法) [20], many-objective evolutionary algorithm based on directional diversity and favorable convergence (基于方向多样性和良好收敛性的多目标进化算法) [21], and knee point driven evolutionary algorithm (KnEA) (拐点驱动的进化算法)[22].

2. 基于指标

• 第二类直接采用表现指标作为选择标准，以区分传统帕累托支配无法区分的非支配解决方案。 在许多其他文献[23]-[26]中，some representative approaches of this category are indicator-based evolutionary algorithm [27], S-metric selection based evolutionary multiobjective optimization algorithm [28], and hypervolume (HV)-based evolutionary algorithm [29].（此类的一些代表性方法是基于指标的进化算法[27]，基于S度量选择的进化多目标优化算法[28]和基于超体积（HV）的进化算法[29]。)

3. 基于分解

• 基于分解的算法是将一个超多目标优化问题分解为一系列简单的子问题并且以协作的方式解决他们。更确切的说，分解的方法是将多目标问题分解为一系列单目标优化问题(SOPs).最流行的基于分解的算法是MOEA/D[30]以及其变体稳定匹配模型的MOEA/D(stable matching model based MOEA/D [31]), MOEA/D with adaptive weight vector adjustment[32], external archive guided MOEA/D [33], MOEA/D with a distance-based updating [34], and online diversity metric based MOEA/D [35]. 另一种分解的方法是将一个超多目标优化问题分解为一系列简单的多目标优化问题 Some representative MOEAs of this type are MOEA/D-M2M [36], reference-point based many-objective NSGA-II (NSGA-III) [37] (参考点), dominance and decomposition (支配和分解) based MOEA [38], and the recently proposed reference vector (参考向量) guided evolutionary algorithm [39].

4. 将一个超多目标优化的问题转化为多目标优化问题
   这个方向有两个分支

• 使用目标缩减的方法消除多余和不相关的目标 such as dominance relation preservation based algorithms （基于优势关系保存的算法）[40], [41], unsupervised feature selection based algorithms （无监督特征选择算法） [42], Pareto corner search based algorithms （基于帕累托角的搜索算法） [43], machine learning based objective reduction （基于机器学习的目标缩减） [44]–[46], and the recently proposed nonlinear correlation information entropy based objective reduction （基于非线性相关信息熵的目标缩减） [47].
• 使用两到三个新定义的目标替换原来的目标 Representative approaches of this type include bi-goal evolution [48] and summation of normalized objective values and diversified selection based MOEA （归一化目标值的总和和多样化选择的MOEA）[49].

5. 提高计算性能

• （个人认为：提高搜索性能和提高计算性能是不一样的，搜索性能关注的是一次评价时种群性能指标的改变；而计算性能指的是评价一次或者计算指标时的时间消耗，或者说是计算量的消耗，也可以认为是时间复杂度，属于算法层面的优化）
• For example, Bringmann et al. [50] suggested to use the Monte Carlo method to improve the computational efficiency of HV calculations in the multiobjective covariance matrix adaptation evolution strategy(提出使用蒙特卡罗方法提高CMA-ES计算HV时的计算效率). Some fast nondominated sorting approaches were also developed to reduce the computational cost of （快速非支配排序算法提高排序效率）Pareto-based MOEAs for solving MaOPs, such as deductive sort [51], corner sort [52], M-front [53], efficient nondominated sort (ENS) [54], and approximate nondominated sort [55].
• 但是值得一提的是还是很少有人关注超多目标算法中的决策变量规模问题，大规模决策变量在单目标中已经研究的很多[56]-[62]，但是在超多目标中还是研究的比较少。[63]
• 最近Ma[64]提出了一种使用决策变量分析方法来对决策变量进行分类的MOEA-MOEA/DVA来解决大规模MOPs。在MOEA/DVA中，基于支配关系的决策变量分析方法把决策变量分为1) 收敛相关变量，2）多样性相关 3）收敛性和多样性都相关。收敛性和多样性相关的变量将使用不同的进化算子进行优化，其中两者都相关的变量将视为多样性相关的变量 本文认为这种方法即使适用于两到三个目标的问题但是对于超多目标的问题的能力还没有得到验证
• 遵循[64]中提出的MOEA / DVA的基本思想，本文提出了一种基于决策变量聚类方法的大规模MaOPs进化算法，主要的新贡献总结如下。

1. 本文中提出的基于k-means的聚类算法根据采样的解和收敛方向的夹角将决策变量分为收敛性和多样性的变量，更小的夹角意味着变量对收敛的作用更大，更大的夹角意味着变量对多样的作用更大。而MOEA/DVA则是基于支配关系，并且提出的方法只会将变量分为收敛和多样性两种变量而MOEA/DVA则含有又收敛又多样的变量。
2. 提出了算法LMEA，并且对于多样性和收敛性方法采用了两种不同的算子。这两种策略都先使用非支配培训作为第一步，然后对于收敛性变量选择策略是基于和理想点的欧式距离（此处设置的是目标空间的原点为理想点，假设优化的都是最小化的问题），对于多样性变量，第二步选择策略依赖的是候选解的角度。
3. 提出基于树的快速非支配排序算法T-ENS，这是ENS[54]的改进版本。在T-ENS中，用于识别非支配关系的信息被记录在树的节点中，由此可以推断出解之间大量的非支配关系。 最终，只需要比较非支配前沿支配的解的子集，而不是全部。 理论分析表明，所提出的T-ENS的时间复杂度为O（MNlogN / logM），其中N表示人口规模，M表示目标数量，这要比目前大多数算法O（MN^2）的时间复杂度小很多。
4. 实验在MaOPs和大规模的MOP上进行，其中大规模的维度有5000

• 本文的其余部分安排如下。 在第二节中，简要回顾了有关解决大规模MOP的MOEA的一些相关工作。 在第二部分中，针对最近提出的MOEA/DVA，阐述了本文动机。 在第三部分中，我们描述本文针对大规模MaOP提出的LMEA的详细信息。 在第四部分中给出了仿真结果，以评估LMEA在大规模MaOP上的性能。 最后，结论和今后的工作在第五节中给出。

相关工作和本文动机

• 在本节中，我们首先回顾一些解决规模MOP的代表性MOEA，然后通过两个说明性示例详细阐述本文的动机。 请注意，当前仅仅有少量文献涉及大规模MOPs,大部分MOEA不是为大规模决策变量MOPs准备的。
• Antonio和Coello [63]提出了一个基于合作的协同进化框架来解决大规模的MOP。 该算法的主要思想是将大量决策变量随机分为相等大小的几个小子组件，并在预定数量的周期内共同协作演化这些子组件。 实验结果证实了该算法在具有两个和三个目标的大规模MOP上的竞争力。 遵循这一思路，在[65]中，合作协同进化的思想也被用来处理大规模的多目标电容弧布线问题。
• 最近，Ma等[64]人提出了一种用于解决大规模MOP的MOEA，称为MOEA / DVA。，其中采用决策变量分析策略，通过检查扰动变量值生成的解之间的优势关系，将决策变量分为不同的组。 具体而言，判定变量的方法如下。

1. 收敛相关的变量，基于扰动生成的解相互支配
2. 多样相关的变量，基于扰动生成的解相互之间非支配
3. 收敛和多样都相关的变量

• 对于不同的变量使用一种两阶段的优化方式来进行优化，对于收敛性相关的变量会被优化直到接近帕累托前沿，而多样性相关的变量会产生一个尽可能大的分布。
• 注意，本篇文章认为MOEA/DVA中收敛相关和多样相关的变量都会被认为是多样相关的变量，这种做法是不合适的，本文提出的算法就只会将决策变量分为两类，这大大提升了算法的收敛性和多样性。
• 下面举一个例子:
  
• 再举一个例子，即使在MOEA/DVA中被视为很明显的和多样性相关的变量实际上为了保证算法的快速收敛有时也需要被考虑成收敛性变量进行优化。例如在例子2中将x2视为收敛性变量能更有效地驱使算法向前沿收敛。
  
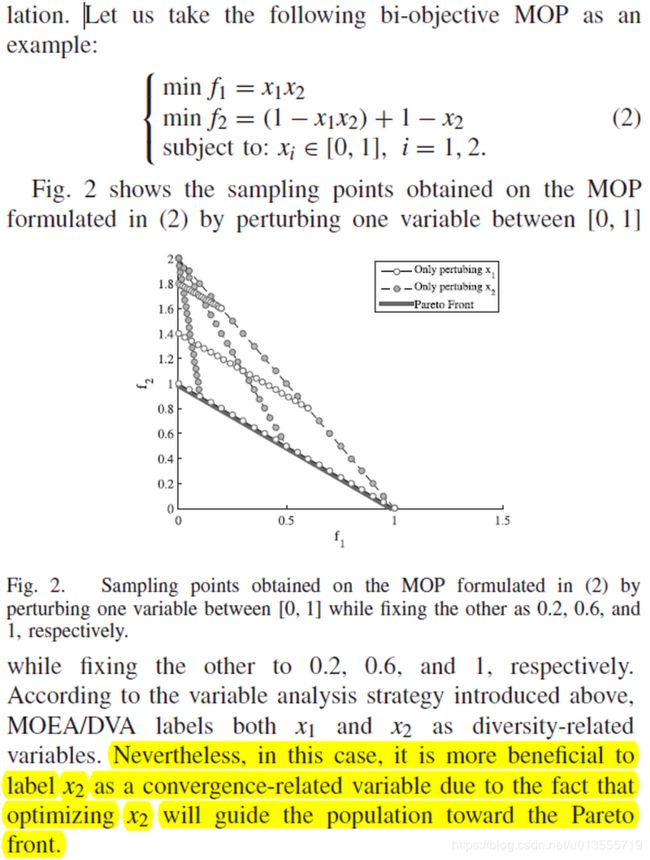
• 为了解决上述问题，本文提出了一种针对大规模MaOP的基于决策变量聚类的MOEA，称为LMEA。 在LMEA中，提出了一种决策变量聚类方法，通过分别测量它们对收敛和多样性的贡献来区分收敛相关和多样性相关的变量。 使用提出的决策变量聚类方法，可以正确地分类与以上两个示例中的x2相似的变量。

提出的算法LMEA

• 首先展示了LMEA的主要算法流程和两个重要组件-决策变量聚类方法和基于树的快速非支配排序

LMEA的主要结构

• 算法1提出了LMEA的主要框架，该框架由以下五个组件组成。首先，随机初始化N个候选解的种群。其次，采用改进的决策变量聚类方法将变量分为两组，收敛相关变量和多样性相关变量。第三，基于这些变量之间的交互作用，与 收敛相关的变量 (注意，这里只谈了收敛性相关的变量进行分组，但是对多样性相关的变量没有要求) 进一步分为几个子组，其中，这些变量在一个子组内彼此交互，但不与其他任何子组内的交互 这个做法采用的是[64]中提出的方法，使用变量分析的策略将收敛性变量分组，子组内变量相互交互，而组与组之间的变量互不相关可以单独进行优化 。每个子组中的变量也称为交互变量，因为由于彼此之间的交互而无法单独优化它们。算法2给出了收敛性相关变量相互作用分析的细节，它采用了[64]中开发的策略。注意，类似的策略也已广泛用于单目标大规模优化中的变量交互检测[56]，[66]。 这里意思是说，这种方法已经很广泛使用了

然后对于收敛性相关的变量采用变量分析的方法将其分组

• 值得注意的是，这是文献[64]提出的一种方式，是利用变量分析法，将相互交互的决策变量分到一个子组中，而各组之间保持变量不交互的状态方便独立优化，具体的变量分析方法可以参见[64].

收敛性变量的优化

1. 非支配排序
2. 计算每个解和理想点之间距离(原点)
3. 进化每个子组中的收敛性变量以获得后代
   3.1. 对于每个子组的变量，从P中二进制锦标赛挑两个解做父代，只将这个维度变量交叉其余维度不变生成子代 ， 子代父代根据收敛性能优胜劣汰 （不同层比层数，层数越低越好，同层比较离理想点的距离，越近越好！）

多样性变量的优化

1. 将所有多样性相关的变量视为一个整体，对这所有的变量进行一次性的交叉(这和收敛性变量一次一个进行优化是不同的)从种群P中生成|P|个后代，然后将子代种群和父代种群混合，并从中挑选出后代。
2. 按照非支配层的观点从合种群中挑选出子代解，如果到达K层时留下的个体总数量超过|P|，则在K层挑选出多样性较好的解。 注意，这里的多样性不是使用拥挤距离进行衡量而是使用目标空间中候选解之间的角度 这个多样性的规则详情要看[39]

基于聚类的决策变量分类方法

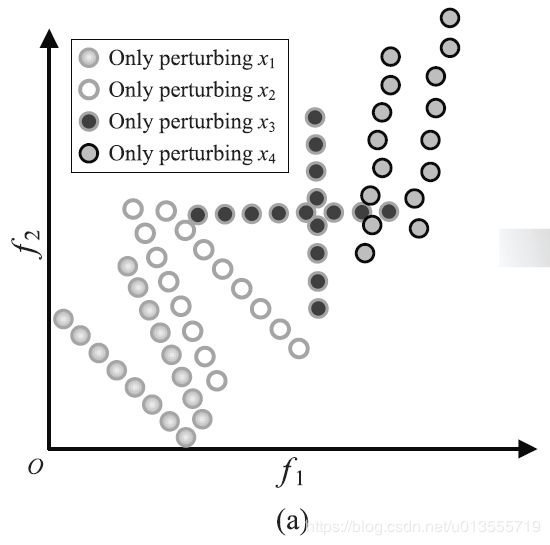
• 图3(a) 显示了这种聚类分类的方法，不同颜色线表示改变调查的不同的变量，相同颜色的条数表示从种群中采样的个体数目，例如，白色的线条有两条就是x2的采样个数是两个个体，而同一条线上点的个数表示对个体上这个变量采取的扰动的数量，例如这里对于单个个体的研究变量的扰动数目为8，所以一条线上的点的个数为8，同时，其他没有考虑的变量此时保持不变。
  
• 图3(b)显示了聚类的标准，就是当考虑同一个变量的改变时，两个解构成的线分别与收敛方向构成的夹角，夹角较大表明变量与多样更相关，而夹角越小表明变量与收敛更相关。
  
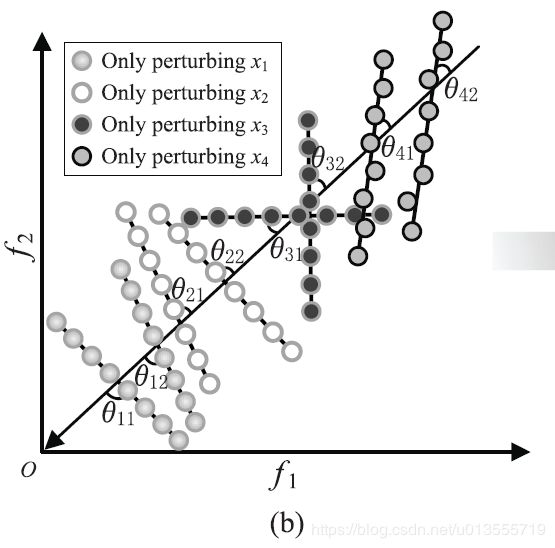
• 图3© 显示了聚类的操作方法，由于考虑的变量的采样解的个数为二，因此构成的是一个二维的坐标系，通过这个坐标系上点的分布而通过K-means将变量分为两个簇、对于考虑多个采样，角度都比较大的变量划归为多样性相关的变量，而对于考虑多个采样，角度都比较小的变量划归为收敛性相关的变量。这种方式而言，单个变量采样的数量越多，坐标系的维度越大，聚类的效果越好！
  
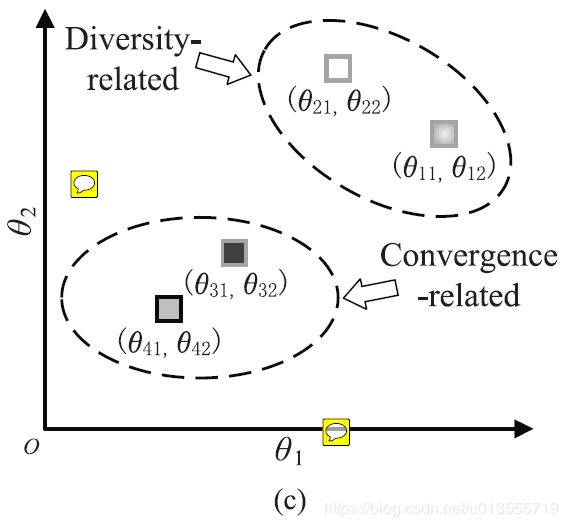
• 图3.示例，说明了如何针对具有四个决策变量（分别为x1，x2，x3和x4）的双目标最小化问题在LMEA中识别收敛相关变量和多样相关变量。 在此示例中，在LMEA中x1和x2被标识为与多样性相关的变量，x3和x4被标识为与收敛相关的变量。 （a）由扰动产生的采样解的目标值。 （b）拟合线和超平面法线之间的角度。 （c）对四个决策变量x1，x2，x3和x4进行聚类结果。
• 图3给出了一个示例，以说明所提出的决策变量聚类方法的主要思想，其中考虑了具有四个决策变量x1，x2，x3和x4的双目标最小化问题。 为了确定决策变量是收敛性相关还是多样性相关性，首先从总体中随机选择多个nSel（在此示例中为两个）候选解决方案。 然后，对所选候选解的四个变量中的每个变量执行多个nPer（在此示例中为8）扰动。 图3（a）描绘了由扰动产生的采样解的目标值。
• 然后，通过扰动每个变量的值的采样解被标准化，生成一条线L以拟合每组标准化样品解。使用归一化的样品解和拟合线L，计算每个拟合线L与超平面f1 +··+ fM = 1的法线之间的夹角，其中法线表示收敛方向，M是 目标。这样，每个变量都会有几个角度相关联，这个数量和挑选的采样解的数量相关（此处为2）
• 最后图3©中表示的是按照角度进行的聚类方法。

和MOEA/DVA的不同

• MOEA/DVA将变量分为三类，其中有一类是既和多样性相关也和收敛性相关的变量。而此方法只会将变量分为两类，即与收敛性相关的变量和与多样性相关的变量，MOEA/DVA中的第三类变量会被分类为多样性或者收敛性相关中的其中一类。并且MOEA/DVA中某些多样性相关的变量也会被识别为收敛性相关的变量。
• MOEA / DVA中的决策变量分析方法根据支配关系确定每个变量的类别。 相比之下，所提出的决策变量聚类方法采用k-means方法来确定每个变量的类别。 与MOEA / DVA中的决策变量分析方法相比，所提出的决策变量聚类方法更健壮，因为其性能独立于基于支配的关系，由于支配抗性问题，基于支配的关系在许多目标优化中可能无效。

参考文献

[1] P. J. Fleming, R. C. Purshouse, and R. J. Lygoe, “Many-objective optimization: An engineering design perspective,” in Proc. 3rd Int. Conf. Evol. Multi Criterion Optim., Guanajuato, Mexico, 2005, pp. 14–32.
[2] J. Garcia, A. Berlanga, and J. M. M. López, “Effective evolutionary algorithms for many-specifications attainment: Application to air traffic control tracking filters,” IEEE Trans. Evol. Comput., vol. 13, no. 1, pp. 151–168, Feb. 2009.
[3] J. B. Kollat, P. M. Reed, and R. M. Maxwell, “Many-objective groundwater monitoring network design using bias-aware ensemble Kalman filtering, evolutionary optimization, and visual analytics,” Water Resources Res., vol. 47, no. 2, pp. 1–18, 2011.
[4] J. W. Kruisselbrink et al., “Combining aggregation with Pareto optimization: A case study in evolutionary molecular design,” in Proc. 5th Int. Conf. Evol. Multi Criterion Optim., Nantes, France, 2009, pp. 453–467.
[5] K. Ikeda, H. Kita, and S. Kobayashi, “Failure of Pareto-based MOEAs: Does non-dominated really mean near to optimal?” in Proc. IEEE Congr. Evol. Comput., Seoul, South Korea, 2001, pp. 957–962.
[6] V. Khare, X. Yao, and K. Deb, “Performance scaling of multiobjective evolutionary algorithms,” in Proc. 2nd Int. Conf. Evol. Multi Criterion Optim., Faro, Portugal, 2003, pp. 376–390.
[7] D. Brockhoff et al., “On the effects of adding objectives to plateau functions,” IEEE Trans. Evol. Comput., vol. 13, no. 3, pp. 591–603, Jun. 2009.
[8] R. C. Purshouse and P. J. Fleming, “Evolutionary many-objective optimisation: An exploratory analysis,” in Proc. Congr. Evol. Comput., Canberra, ACT, Australia, 2003, pp. 2066–2073.
[9] R. C. Purshouse and P. J. Fleming, “On the evolutionary optimization of many conflicting objectives,” IEEE Trans. Evol. Comput., vol. 11, no. 6, pp. 770–784, Dec. 2007.
[10] S. Chand and M. Wagner, “Evolutionary many-objective optimization: A quick-start guide,” Surveys Oper. Res. Manag. Sci., vol. 20, no. 2, pp. 35–42, 2015.
[11] B. Li, J. Li, K. Tang, and X. Yao, “Many-objective evolutionary algorithms: A survey,” ACM Comput. Surveys, vol. 48, no. 1, pp. 1–37, 2015.
[12] M. Laumanns, L. Thiele, K. Deb, and E. Zitzler, “Combining convergence and diversity in evolutionary multiobjective optimization,” Evol. Comput., vol. 10, no. 3, pp. 263–282, 2002.
[13] D. Hadka and P. Reed, “Borg: An auto-adaptive many-objective evolutionary computing framework,” Evol. Comput., vol. 21, no. 2, pp. 231–259, 2013.
[14] X. Zou, Y. Chen, M. Liu, and L. Kang, “A new evolutionary algorithm for solving many-objective optimization problems,” IEEE Trans. Syst., Man, Cybern. B, Cybern., vol. 38, no. 5, pp. 1402–1412, Oct. 2008.
[15] G. Wang and H. Jiang, “Fuzzy-dominance and its application in evolutionary many objective optimization,” in Proc. Int. Conf. Comput. Intell. Security Workshops, Harbin, China, 2007, pp. 195–198.
[16] F. di Pierro, S.-T. Khu, and D. A. Savi´c, “An investigation on preference order ranking scheme for multiobjective evolutionary optimization,” IEEE Trans. Evol. Comput., vol. 11, no. 1, pp. 17–45, Feb. 2007.
[17] Y. Yuan, H. Xu, B. Wang, and X. Yao, “A new dominance relationbased evolutionary algorithm for many-objective optimization,” IEEE Trans. Evol. Comput., vol. 20, no. 1, pp. 16–37, Feb. 2016.
[18] M. Köppen and K. Yoshida, “Substitute distance assignments in NSGA-II for handling many-objective optimization problems,” in Proc. 4th Int. Conf. Evol. Multi Criterion Optim., Matsushima, Japan, 2007, pp. 727–741.
[19] S. Yang, M. Li, X. Liu, and J. Zheng, “A grid-based evolutionary algorithm for many-objective optimization,” IEEE Trans. Evol. Comput., vol. 17, no. 5, pp. 721–736, Oct. 2013.
[20] R. Wang, R. C. Purshouse, and P. J. Fleming, “Preference-inspired coevolutionary algorithms for many-objective optimization,” IEEE Trans. Evol. Comput., vol. 17, no. 4, pp. 474–494, Aug. 2013.
[21] J. Cheng, G. G. Yen, and G. Zhang, “A many-objective evolutionary algorithm with enhanced mating and environmental selections,” IEEE Trans. Evol. Comput., vol. 19, no. 4, pp. 592–605, Aug. 2015.
[22] X. Zhang, Y. Tian, and Y. Jin, “A knee point-driven evolutionary algorithm for many-objective optimization,” IEEE Trans. Evol. Comput., vol. 19, no. 6, pp. 761–776, Dec. 2014.
[23] C. A. R. Villalobos and C. A. C. Coello, “A new multi-objective evolutionary algorithm based on a performance assessment indicator,” in Proc. 14th Annu. Conf. Genet. Evol. Comput. (GECCO), Philadelphia, PA, USA, 2012, pp. 505–512.
[24] T. Ulrich, J. Bader, and L. Thiele, “Defining and optimizing indicatorbased diversity measures in multiobjective search,” in Proc. 11th Int. Conf. Parallel Problem Solving Nat., Kraków, Poland, 2010, pp. 707–717.
[25] H. Trautmann, T. Wagner, and D. Brockhoff, “R2-EMOA: Focused multiobjective search using R2-indicator-based selection,” in Proc. 7th Int. Conf. Learn. Intell. Optim., Catania, Italy, 2013, pp. 70–74.
[26] G. Rudolph, O. Schütze, C. Grimme, and H. Trautmann, “An aspiration set EMOA based on averaged hausdorff distances,” in Proc. 8th Int. Conf. Learn. Intell. Optim., Gainesville, FL, USA, 2014, pp. 153–156.
[27] E. Zitzler and S. Künzli, “Indicator-based selection in multiobjective search,” in Proc. 8th Int. Conf. Parallel Problem Solving Nat., Birmingham, U.K., 2004, pp. 832–842.
[28] N. Beume, B. Naujoks, and M. Emmerich, “SMS-EMOA: Multiobjective selection based on dominated hypervolume,” Eur. J. Oper. Res., vol. 181, no. 3, pp. 1653–1669, 2007.
[29] J. Bader and E. Zitzler, “HypE: An algorithm for fast hypervolume-based many-objective optimization,” Evol. Comput., vol. 19, no. 1, pp. 45–76, 2011.
[30] Q. Zhang and H. Li, “MOEA/D: A multiobjective evolutionary algorithm based on decomposition,” IEEE Trans. Evol. Comput., vol. 11, no. 6, pp. 712–731, Dec. 2007.
[31] K. Li, Q. Zhang, S. Kwong, M. Li, and R. Wang, “Stable matching-based selection in evolutionary multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 18, no. 6, pp. 909–923, Dec. 2014.
[32] Y. Qi et al., “MOEA/D with adaptive weight adjustment,” Evol. Comput., vol. 22, no. 2, pp. 231–264, 2014.
[33] X. Cai, Y. Li, Z. Fan, and Q. Zhang, “An external archive guided multiobjective evolutionary algorithm based on decomposition for combinatorial optimization,” IEEE Trans. Evol. Comput., vol. 19, no. 4, pp. 508–523, Aug. 2015.
[34] Y. Yuan, H. Xu, B. Wang, B. Zhang, and X. Yao, “Balancing convergence and diversity in decomposition-based many-objective optimizers,” IEEE Trans. Evol. Comput., vol. 20, no. 2, pp. 180–198, Apr. 2016.
[35] S. B. Gee, K. C. Tan, V. A. Shim, and N. R. Pal, “Online diversity assessment in evolutionary multiobjective optimization: A geometrical perspective,” IEEE Trans. Evol. Comput., vol. 19, no. 4, pp. 542–559, Aug. 2015.
[36] H.-L. Liu, F. Gu, and Q. Zhang, “Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems,” IEEE Trans. Evol. Comput., vol. 18, no. 3, pp. 450–455, Jun. 2014.
[37] K. Deb and H. Jain, “An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints,” IEEE Trans. Evol. Comput., vol. 18, no. 4, pp. 577–601, Aug. 2014.
[38] K. Li, K. Deb, Q. Zhang, and S. Kwong, “An evolutionary many-objective optimization algorithm based on dominance and decomposition,” IEEE Trans. Evol. Comput., vol. 19, no. 5, pp. 694–716, Oct. 2015.
[39] R. Cheng, Y. Jin, M. Olhofer, and B. Sendhoff, “A reference vector guided evolutionary algorithm for many-objective optimization,” IEEE Trans. Evol. Comput., to be published.
[40] D. Brockhoff and E. Zitzler, “Are all objectives necessary? On dimensionality reduction in evolutionary multiobjective optimization,” in Proc. 9th Int. Conf. Parallel Problem Solving Nat., Reykjavik, Iceland, 2006, pp. 533–542.
[41] D. Brockhoff and E. Zitzler, “Objective reduction in evolutionary multiobjective optimization: Theory and applications,” Evol. Comput., vol. 17, no. 2, pp. 135–166, 2009.
[42] A. L. Jaimes, C. A. C. Coello, and D. Chakraborty, “Objective reduction using a feature selection technique,” in Proc. 10th Annu. Conf. Genet. Evol. Comput., Atlanta, GA, USA, 2008, pp. 673–680.
[43] H. K. Singh, A. Isaacs, and T. Ray, “A Pareto corner search evolutionary algorithm and dimensionality reduction in many-objective optimization problems,” IEEE Trans. Evol. Comput., vol. 15, no. 4, pp. 539–556, Aug. 2011.
[44] K. Deb and D. Saxena, “Searching for Pareto-optimal solutions through dimensionality reduction for certain large-dimensional multi-objective optimization problems,” in Proc. World Congr. Comput. Intell., Vancouver, BC, Canada, 2006, pp. 3352–3360.
[45] D. K. Saxena and K. Deb, “Non-linear dimensionality reduction procedures for certain large-dimensional multi-objective optimization problems: Employing correntropy and a novel maximum variance unfolding,” in Proc. 4th Int. Conf. Evol. Multi Criterion Optim., Matsushima, Japan, 2007, pp. 772–787.
[46] D. K. Saxena, J. A. Duro, A. Tiwari, K. Deb, and Q. Zhang, “Objective reduction in many-objective optimization: Linear and nonlinear algorithms,” IEEE Trans. Evol. Comput., vol. 17, no. 1, pp. 77–99, Feb. 2013.
[47] H. Wang and X. Yao, “Objective reduction based on nonlinear correlation information entropy,” Soft Comput., vol. 20, no. 6, pp. 2393–2407, 2016.
[48] M. Li, S. Yang, and X. Liu, “Bi-goal evolution for many-objective optimization problems,” Artif. Intell., vol. 228, pp. 45–65, Nov. 2015.
[49] B.-Y. Qu and P. N. Suganthan, “Multi-objective evolutionary algorithms based on the summation of normalized objectives and diversified selection,” Inf. Sci., vol. 180, no. 17, pp. 3170–3181, 2010.
[50] K. Bringmann, T. Friedrich, C. Igel, and T. Voß, “Speeding up manyobjective optimization by Monte Carlo approximations,” Artif. Intell., vol. 204, pp. 22–29, Nov. 2013.
[51] K. McClymont and E. Keedwell, “Deductive sort and climbing sort: New methods for non-dominated sorting,” Evol. Comput., vol. 20, no. 1, pp. 1–26, Mar. 2012.
[52] H. Wang and X. Yao, “Corner sort for Pareto-based many-objective optimization,” IEEE Trans. Cybern., vol. 44, no. 1, pp. 92–102, Jan. 2014.
[53] M. Drozdík, Y. Akimoto, H. Aguirre, and K. Tanaka, “Computational cost reduction of nondominated sorting using the M-front,” IEEE Trans. Evol. Comput., vol. 19, no. 5, pp. 659–678, Oct. 2015.
[54] X. Zhang, Y. Tian, R. Cheng, and Y. Jin, “An efficient approach to nondominated sorting for evolutionary multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 19, no. 2, pp. 201–213, Apr. 2015.
[55] X. Zhang, Y. Tian, and Y. Jin, “Approximate non-dominated sorting for evolutionary many-objective optimization,” Inf. Sci., Jun. 2016.
[56] Z. Yang, K. Tang, and X. Yao, “Large scale evolutionary optimization using cooperative coevolution,” Inf. Sci., vol. 178, no. 15, pp. 2985–2999, 2008.
[57] M. N. Omidvar, X. Li, Y. Mei, and X. Yao, “Cooperative co-evolution with differential grouping for large scale optimization,” IEEE Trans. Evol. Comput., vol. 18, no. 3, pp. 378–393, Jun. 2014.
[58] X. Li and X. Yao, “Cooperatively coevolving particle swarms for large scale optimization,” IEEE Trans. Evol. Comput., vol. 16, no. 2, pp. 210–224, Apr. 2012.
[59] R. Cheng and Y. Jin, “A competitive swarm optimizer for large scale optimization,” IEEE Trans. Cybern., vol. 45, no. 2, pp. 191–204, Feb. 2015.
[60] K. H. Hajikolaei, Z. Pirmoradi, G. H. Cheng, and G. G. Wang, “Decomposition for large-scale global optimization based on quantified variable correlations uncovered by metamodelling,” Eng. Optim., vol. 47, no. 4, pp. 429–452, 2015.
[61] J. Fan, J. Wang, and M. Han, “Cooperative coevolution for largescale optimization based on kernel fuzzy clustering and variable trust region methods,” IEEE Trans. Fuzzy Syst., vol. 22, no. 4, pp. 829–839, Aug. 2014.
[62] R. Cheng and Y. Jin, “A social learning particle swarm optimization algorithm for scalable optimization,” Inf. Sci., vol. 291, pp. 43–60, Jan. 2015.
[63] L. M. Antonio and C. A. C. Coello, “Use of cooperative coevolution for solving large scale multiobjective optimization problems,” in Proc. IEEE Congr. Evol. Comput., Cancún, Mexico, 2013, pp. 2758–2765.
[64] X. Ma et al., “A multiobjective evolutionary algorithm based on decision variable analyses for multiobjective optimization problems with largescale variables,” IEEE Trans. Evol. Comput., vol. 20, no. 2, pp. 275–298, Apr. 2016.
[65] R. Shang, K. Dai, L. Jiao, and R. Stolkin, “Improved memetic algorithm based on route distance grouping for multiobjective large scale capacitated arc routing problems,” IEEE Trans. Cybern., vol. 46, no. 4, pp. 1000–1013, Apr. 2016.
[66] W. Chen, T. Weise, Z. Yang, and K. Tang, “Large-scale global optimization using cooperative coevolution with variable interaction learning,” in Proc. 11th Int. Conf. Parallel Problem Solving Nat., Kraków, Poland, 2010, pp. 300–309.
[67] K. Deb and R. B. Agrawal, “Simulated binary crossover for continuous search space,” Complex Systems, vol. 9, no. 4, pp. 115–148, 1995.
[68] K. Deb and M. Goyal, “A combined genetic adaptive search (GeneAS) for engineering design,” Comput. Sci. Informat., vol. 26, no. 4, pp. 30–45, 1996.
[69] B. V. Babu and M. M. L. Jehan, “Differential evolution for multi-objective optimization,” in Proc. Congr. Evol. Comput., vol. 4. Canberra, ACT, Australia, 2003, pp. 2696–2703.