《高维数据的聚类分析研究及其应用》读书笔记

一、高维聚类の研究方向

        由于高维数据的稀疏性等特征，使得在高维聚类的研究中有如下几个研究重点：

1）维度约简，主要分为特征变换和特征选择两大类。前者是对特征空间的变换映射，常见的有PCA、SVD等。后者则是选择特征的子集，常见的搜索方式有自顶向下、随机搜索等；

2）高维聚类算法，主要分为高维全空间聚类和子空间聚类算法。前者的研究主要聚焦在对传统聚类算法的优化改进上，后者则可以看做维度约简的推广；

3）聚类有效性，是对量化评估方法的研究；

4）聚类结果表示方法；

5）高维数据索引结构；

6）高维离群点的研究...

二、该论文主要贡献

        该论文主要聚类于维度约简和聚类初始中心点选择两方面，前者作者提出了基于多层过滤的方法：先将特征重要度作为启发式信息来对遗传算法的初始群体进行优化，而后利用粗糙集的特性。对后者的研究，作者提出了一种基于点的局部密度的簇中心点初始化机制。同时，作者还提出了一种新的局部密度因子度量SNDF。

三、传统聚类方法

1.基于划分的方法

         即给定一个数据集，将其划分为k个子集，每个子集代表一个聚类。基于划分的聚类方法包括K-means、K-medoids、K-modes、CLARA等。

2.基于层次的聚类

        基于层次的聚类方法按照分裂或合并的原则，为数据集构造层次聚类树，根据终止条件得到聚类树某个层次上的聚类结果。根据树的构造方法可以分为如下两类：

3.基于密度的聚类

         即使用密度来描述数据点之间的相似度，并将簇看做是数据空间中被低密度区域分隔开的高密度对象区域，而低密度区域中的数据点为噪声。

4.基于网格的方法

         即将对象空间划分为有限数目的单元以形成网络结构。

5.基于模型的方法

         即为每个聚类假设一个模型，然后再去发现符合相应模型的数据对象。它根据标准统计方法并考虑到“噪声”或异常数据，可以自动确定聚类个数，因此有很好的鲁棒性。

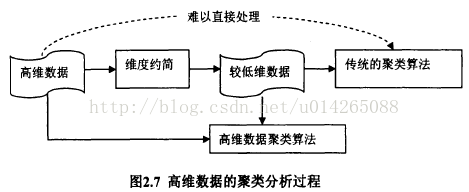
四、高维数据聚类分析

1.分析过程

、

2.维度约简

         一方面，“维度效应”使得数据点之间的密度和距离的定义变得不太有意义；另一方面，冗余和不相关的特征将导致聚类质量下降。

         1）特征变换

                  即在输入特征空间上做变换(如线性变换等)得到新的特征空间。该方法生成新的特征(可解释性和可理解性变差)，但本质上并没有删除不相关或冗余特征。

         2）特征选择

                  即从原始特征空间中选择一个优化的特征子集参与聚类。根据特征选择过程中是否有类标签参与，分为有指导和无指导两类方法。

3.高维数据聚类算法

          1）全空间聚类

                  全空间聚类的一个主要类别是基于维度空间的变换，即聚类算法本身将高维空间上的问题映射到低维空间或更高维的数据空间中寻找簇。如基于超图模型的方法使用“频繁项集支持度”度量多个对象之间的相似度,从而将高维数据聚类问题转换为超图分割寻优的问题。基于核的聚类方法用核函数将原始空间的对象映射到更高维的特征空间，以此放大高维数据点间的差异来进行更准确的聚类。

                  另一个方法主要是基于改进的传统聚类算法。

         2）子空间聚类

                  目前为止,所考虑的高维聚类算法都是基于所有的特征来发现簇。子空间聚类是从另一个角度处理高维数据聚类。由于不同的簇可能与不同的子空间特征子集相关联,一些算法就把原始全空间划分为不同的子空间,从子空间考察聚类的存在,并在聚类的过程中为每个簇寻找相应的特征子集。与全空间的维度约简方法相对应,子空间聚类算法实际上可以看作是一种局部维度约简方法。

五、特征选择算法

         关于特征选择算法的研究主要集中在两方面：如何有效地产生候选特征子集（特征搜索策略），以及如何评价特征子集。另外，不同的应用环境需要制定相应的搜索策略和特征度量准则来实现高效的特征降维。

六、高维数据的聚类初始化方法

         多数传统的初始化方法是基于全空间的距离或数据点密度进行，并且传统的初始化方法无法排除“噪声点”和“离群点”的影响。

1.传统的初始化方法

         1）基于随机抽取初始化方法

                  虽然这类方法是普遍使用的基本方法,然而所生成的随机初始聚类中心可能会导致聚类算法迭代最终在局部最优的结果上。除此之外,随机初始化很容易选中噪声点或离群点作为初始聚类质心,进而影响聚类效率和质量。

         2）基于距离最优的初始化方法

                  很多聚类算法的思想是将簇类内部差异最小化,并且让聚类之间的分离最大化。因此,考虑最优化聚类之间距离即簇中心之间距离增大能够使得聚类后的数据具有满意的分离度。

         3）基于密度评估的初始化方法

                  基于密度的初始化方法是以输入数据满足高斯混合分布的假设为前提的。从而通过识别出输入样本点的密集区域,将这些密集区域的样本点选为初始的聚类 中心点,以此找到密集的聚类。