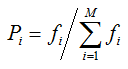智能优化算法求解TSP问题--遗传算法
TSP问题基本概念
TSP问题即旅行商问题(TravelingSalesperson Problem)。该问题给定n个城市和两两城市之间的距离,要求确定一条经过各城市当且仅当一次的最短路线。其图论描述为:给定图G=(V, A),其中V为顶点集,A为各顶点相互连接组成的边集,已知各顶点间的连接距离,要求确定一条长度最短的Hamilton回路,即遍历所有顶点当且仅当一次的最短回路。
遗传算法的基本原理
遗传算法是一类随机优化算法,但它不是简单的随机比较搜索,而是通过对染色体的评价和对染色体中基因的作用,有效地利用已有信息来指导搜索有希望改善优化质量的状态。
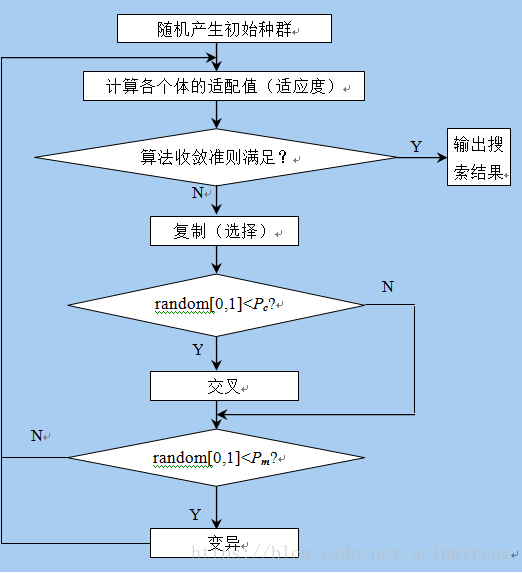
标准遗传算法主要步骤可描述如下:
① 随机产生一组初始个体构成初始种群。
② 计算每一个体的适配值(fitnessvalue,也称为适应度)。适应度值是对染色体(个体)进行评价的一种指标,是GA进行优化所用的主要信息,它与个体的目标值存在一种对应关系。
③ 判断算法收敛准则是否满足,若满足,则输出搜索结果;否则执行以下步骤。
④ 根据适应度值大小以一定方式执行复制操作(也称为选择操作)。
⑤ 按交叉概率pc执行交叉操作。
⑥ 按变异概率pm执行变异操作。
⑦ 返回步骤②。
标准遗传算法流程图下图所示。
1、设计算法的编码方式
路径编码是描述TSP解的最常用的一种策略。所谓路径编码,即直接采用城市在路径中的位置来构造用于优化的状态。
例如:设九城市TSP问题的路径为5-4-1-7-9-8-6-2-3,
对应的路径编码为:(5 4 1 7 9 8 6 23)。
这种编码形式自然直观,易于加入启发式信息,也有利于优化操作的设计。
2、设计遗传算法的适应度函数
对个体i,计算与路径编码相对应的距离,设为di。显然距离值di越大,适应度值应越小。因此,适应度函数可定义为f=1/di。
3、设计遗传算法的选择操作
选择是用来确定交叉个体,以及被选个体将产生多少个子代个体。它是基于适应度值计算基础上进行的。在被选集中,每个个体都有一个选择概率,这个概率由种群中个体的适应度及其分布决定。若某个个体i,其适应度为fi,则其被选取的概率表示为:。
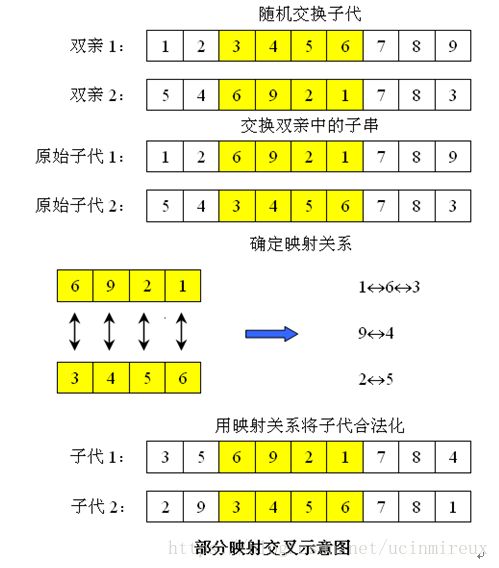
4、设计遗传算法的交叉操作
在选择操作的基础上,根据一定的概率(称为交叉概率)进行交叉操作。交叉的目的是为了能够在下一代产生新的个体,它是遗传算法获取新的优良个体的最重要的手段。交叉操作中,把两个父个体的部分结构进行替换重组,生成新个体。根据个体编码方法的不同可以有不同的算法。
TSP问题中,交叉操作可设计如下:
遗传算法中并不是所有被选择的个体,都要进行交叉操作。交叉概率用于控制交叉操作的频率。概率太大时,种群中串的更新很快,使高适应度值的个体很快被破坏掉。概率太小时,交叉操作很少进行,使搜索停滞不前。
5、设计遗传算法的变异操作
同交叉操作一样,并不是所有被选择的个体,都要进行变异操作。变异概率是加大种群多样性的重要因素,但是概率太小就很难产生新个体,概率太大会使GA成为随机搜索。基于二进制编码的GA中,通常一个较低的变异率足以防止整个群体中任一位置的基因一直保持不变。
TSP问题中,变异操作可设计如下:
6、编写基于遗传算法的TSP问题求解程序
遗传算法的优点和缺点
遗传算法的优点:
与问题领域无关切快速随机的搜索能力;
搜索从群体出发,具有潜在的并行性,可以进行多个个体的同时比较;
搜索使用评价函数启发,过程简单;
使用概率机制进行迭代,具有随机性;
具有可扩展性,容易与其他算法结合。
遗传算法的缺点:
遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码;
另外三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验;
算法对初始种群的选择有一定的依赖性,能够结合一些启发算法进行改进;
算法的并行机制的潜在能力没有得到充分的利用,这也是当前遗传算法的一个研究热点方向。
现在的工作中,遗传算法(1972年提出)已经不能很好的解决大规模计算量问题,它很容易陷入“早熟”。常用混合遗传算法,合作型协同进化算法等来替代,这些算法都是GA的衍生算法。
遗传算法具有良好的全局搜索能力,可以快速地将解空间中的全体解搜索出,而不会陷入局部最优解的快速下降陷阱;并且利用它的内在并行性,可以方便地进行分布式计算,加快求解速度。但是遗传算法的局部搜索能力较差,导致单纯的遗传算法比较费时,在进化后期搜索效率较低。在实际应用中,遗传算法容易产生早熟收敛的问题。采用何种选择方法既要使优良个体得以保留,又要维持群体的多样性,一直是遗传算法中较难解决的问题。
模拟退火算法虽具有摆脱局部最优解的能力,能够以随机搜索技术从概率的意义上找出目标函数的全局最小点。但是,由于模拟退火算法对整个搜索空间的状况了解不多,不便于使搜索过程进入最有希望的搜索区域,使得模拟退火算法的运算效率不高。模拟退火算法对参数(如初始温度)的依赖性较强,且进化速度慢。
对我而言,难点是参数的调节和适应度函数的选择,由于缺乏经验,刚开始参数调节的效果并不太好,但是在不断地改进中,能够获得较好的参数。
从运行结果发现遗传算法的缺点:进化停滞。往往前几代就找到了局部最优解,也就是早熟现象。发现也有很多人对这方面最了改进。比如调整选择算法,在最初几代降低优秀个体差异带来的选择概率,后面增加优秀个体被选择的概率。还有变异时简单的单点变异会造成等位基因的缺失,所以采用两条染色体求同或和异或保证等位基因的多样性。这些都能降低收敛速度。
#include
#include
#include
#include
#include
using namespace std;
const int city_num = 30; //城市个数
#define POPULATION_NUM 2000 //种群数量
#define CROSSOVER_RATE 0.65 //交叉概率
#define ABERRATION_RAET 0.05 //变异概率
#define ITERATIONS 30 //若连续ITERATIONS次解无改进,则退出遗传算法
struct OneRoad{
int path[city_num];//路径信息
double length; //总路径长度
double fit; //适应度
double sum_fit; //累计适应度概率
};//一条路径的信息
OneRoad* road;//定义一个种群
const double city_coord[city_num][2] = {
{ 41, 94 }, { 37, 84 }, { 53, 67 }, { 25, 62 }, { 7, 64 }, { 2, 99 }, { 68, 58 }, { 71, 44 },
{ 54, 62 }, { 83, 69 }, { 64, 60 }, { 18, 54 }, { 22, 60 }, { 83, 46 }, { 91, 38 }, { 25, 38 },
{ 24, 42 }, { 58, 69 }, { 71, 71 }, { 74, 78 }, { 87, 76 }, { 18, 40 }, { 13, 40 }, { 82, 7 },
{ 62, 32 }, { 58, 35 }, { 45, 21 }, { 41, 26 }, { 44, 35 }, { 4, 50 } };//城市坐标
//void ReadFile(); //读取文件
void Init(); //初始化种群
void Evluate(); //计算适应度
void Select(); //选择
void CrossOver(); //交叉函数
void Mutation(); //变异函数
int main(){
//ReadFile();
road = (OneRoad*)malloc(sizeof(OneRoad)*POPULATION_NUM);
Init();
OneRoad allbest, best;
allbest.fit = 0;
best.fit = 0;
clock_t start, end;
int k = 0;
start = clock();
Evluate();
while (k < ITERATIONS){
Select();
Evluate();
CrossOver();
Evluate();
Mutation();
Evluate();
for (int i = 0; i < POPULATION_NUM; i++){
if (best.fit < road[i].fit){
best = road[i];
}
}
if (allbest.fit < best.fit){
allbest = best;
k = 0;
}
else{
k++;
}
}
end = clock();
cout << "最短距离是:" << allbest.length << endl;
cout << "最短路径是:" << endl;
cout << allbest.path[0] + 1;
for (int i = 1; i < city_num; i++)
cout << "->" << allbest.path[i] + 1;
cout << "->" << allbest.path[0] + 1;
cout << endl;
cout << "运行时间是:" << (double)(end - start) / CLOCKS_PER_SEC << "s" << endl;
free(road);
system("pause");
return 0;
}
/*void ReadFile(){
ifstream read_in;
read_in.open("F:\\课程\\智能信息处理\\我的代码\\GA\\GA\\TSP30.txt", ios::in);
if (!read_in.is_open()){
cout << "the file is opened error!" << endl;
return;
}
for (int i = 0; i < city_num; i++){
read_in >> city_coord[i][0] >> city_coord[i][1];
}
read_in.close();
}*/
void Init(){
int i, j;
int t_city;
for (i = 0; i < POPULATION_NUM; i++){
road[i].path[0] = 0;
bool flag[city_num] = {};
for (j = 1; j < city_num; j++){
t_city = rand() % city_num;
while (flag[t_city] || t_city == 0){
t_city = rand() % city_num;
}
flag[t_city] = true;
road[i].path[j] = t_city;
}
}
}
void Evluate(){
int a = 0, b = 0;
double sum = 0;
double x1 = 0, x2 = 0, y1 = 0, y2 = 0;
for (int i = 0; i < POPULATION_NUM; i++){
road[i].length = 0;
for (int j = 0; j < city_num - 1; j++){
a = road[i].path[j];
b = road[i].path[j + 1];
x1 = city_coord[a][0];
y1 = city_coord[a][1];
x2 = city_coord[b][0];
y2 = city_coord[b][1];
road[i].length += sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2));
}
road[i].length += sqrt((city_coord[0][0] - city_coord[city_num - 1][0])*(city_coord[0][0] - city_coord[city_num - 1][0])
+ (city_coord[0][1] - city_coord[city_num - 1][1])*(city_coord[0][1] - city_coord[city_num - 1][1]));
}
for (int i = 0; i < POPULATION_NUM; i++)
{
road[i].fit = 1.0 / road[i].length*1.0 / road[i].length;
sum += road[i].fit;
}
road[0].sum_fit = road[0].fit / sum;
for (int i = 1; i < POPULATION_NUM; i++)
road[i].sum_fit = road[i].fit / sum + road[i - 1].sum_fit;
}
void Select(){
OneRoad* t = (OneRoad*)malloc(sizeof(OneRoad)*POPULATION_NUM);
srand((unsigned)time(NULL));
for (int i = 0; i < POPULATION_NUM; i++)
t[i] = road[i];
for (int i = 0; i < POPULATION_NUM; i++){
double sum = (rand() % 10000) / 9999.0;
for (int j = 0; j < POPULATION_NUM; j++){
if (road[j].sum_fit > sum){
t[i] = road[j];
break;
}
}
}
for (int i = 0; i < POPULATION_NUM; i++){
road[i] = t[i];
}
free(t);
}
void CrossOver(){
OneRoad* t = (OneRoad*)malloc(sizeof(OneRoad)*POPULATION_NUM);
srand((unsigned)time(NULL));
for (int i = 0; i < POPULATION_NUM; i++)
t[i] = road[i];
for (int i = 0; i < POPULATION_NUM - 1; i = i + 2)
{
bool flag[city_num] = {};
double p = (rand() % 10000) / 9999.0;
if (p < CROSSOVER_RATE){
int a = rand() % city_num;
int b = rand() % city_num;
while (a == 0 || b == 0){
a = rand() % city_num;
b = rand() % city_num;
}
if (a > b)swap(a, b);
for (int j = a; j <= b; j++){
t[i].path[j] = road[i].path[j];
flag[road[i].path[j]] = true;
}
int k = 1;
if (a == 1)
k = b + 1;
for (int j = 1; j < city_num; j++){
if (!flag[road[i + 1].path[j]]){
t[i].path[k] = road[i + 1].path[j];
k++;
if (k == a)
k = b + 1;
}
}
}
else{
for (int j = 0; j < city_num; j++){
t[i].path[j] = road[i + 1].path[j];
}
}
}
for (int i = 0; i < POPULATION_NUM - 1; i = i + 2){
for (int j = 0; j < city_num; j++){
road[i].path[j] = t[i].path[j];
}
}
free(t);
}
void Mutation(){
int x1 = 0, x2 = 0;
srand((unsigned)time(NULL));
for (int i = 0; i < POPULATION_NUM; i++){
double p = (rand() % 10000) / 9999.0;
if (p < ABERRATION_RAET){
x1 = rand() % city_num;
x2 = rand() % city_num;
while (x1 == 0 || x2 == 0){
x1 = rand() % city_num;
x2 = rand() % city_num;
}
swap(road[i].path[x1], road[i].path[x2]);
}
}
}