「ARC103D」Robot Arms「构造」

题意

给定\(n\)个点，你需要找到一个合适的\(m\)和\(d_1,d_2,...,d_m\)，使得从原点出发每次向四个方向的某一个走\(d_i\)个单位，最终到达\((x_t, y_t)\)。输出\(m\)和\(d\)数组；对于\(t=1\to n\)输出方向。

\(n \leq 10^3\)，坐标范围\(10^9\)

题解

如果这些点\((x_t, y_t)\)，\(x_t + y_t\)的奇偶性不同那无解

如果\(x_t + y_t\)为偶数，我们先让\(d_1=1\)，这样转换为\(x_t+y_t\)为奇数的情况。

奇数怎么做？二进制构造。

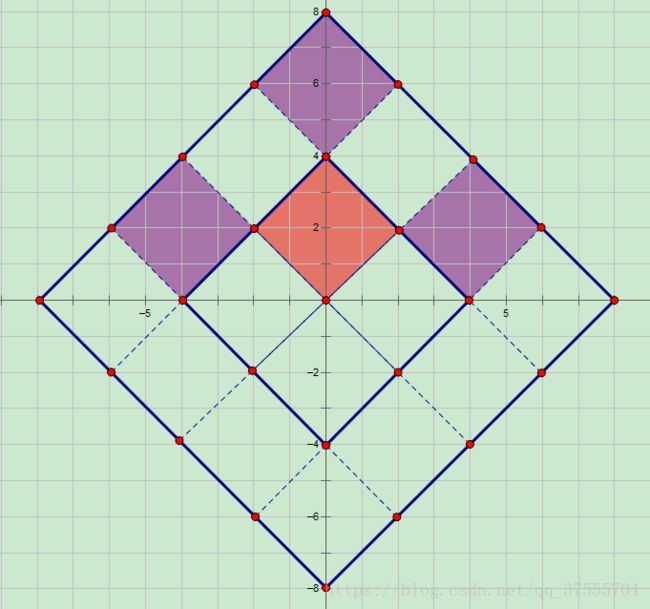
一：考虑\(d(k)={1, 2, 4, ..., 2^k}\)这样的集合，能走到所有\(|x| + |y| \leq 2^{k + 1}-1\)的点（且和为奇数）

证明：https://blog.csdn.net/qq_37555704/article/details/83217444#_14 这里搬来的图。

对于\(d(k) - d(k-1)\)的区域（新区域），直接走一步就到了（如上图红到紫）

对于原来就能到达的区域，我们可以从内部走到内部。

二：考虑怎么找到方案。

证明：\(d(k)\)能走到到点满足\(\min(|x|, |y|) \leq 2^k-1\)

证明大概就是最值在\(|x|=2^k-1,|y|=2^k\)时取到，调整发现不优。

我们只要每次从\(d(k)\)走到\(d(k-1)\)即可，到\(d(0)\)时就成功了

通过画图分析，每次把绝对值大的减小就可以从\(d(k)\)走到\(d(k-1)\)。

那么这个题就没了。还有我们上面是\(d(k)\)走到\(d(k-1)\)，实际上是反过来的，因此输出的字母要注意取反。

#include 
#include 
using namespace std;

const int N = 1010;

int n, m, x[N], y[N], d[N];
bool tg[N];

int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) {
        scanf("%d%d", x + i, y + i);
        tg[(x[i] + y[i]) & 1] = 1;
    }
    if(tg[0] & tg[1]) return puts("-1") & 0;
    if(tg[0]) d[++ m] = 1;
    for(int i = 30; ~ i; i --) d[++ m] = 1 << i;
    printf("%d\n", m);
    for(int i = 1; i <= m; i ++) printf("%d%c", d[i], " \n"[i == m]);
    for(int i = 1; i <= n; i ++, putchar('\n')) {
        for(int j = 1; j <= m; j ++) {
            if(abs(x[i]) > abs(y[i])) {
                if(x[i] > 0) x[i] -= d[j], putchar('R');
                else x[i] += d[j], putchar('L');
            } else {
                if(y[i] > 0) y[i] -= d[j], putchar('U');
                else y[i] += d[j], putchar('D');
            }
        }
    }
    return 0;
}

转载于:https://www.cnblogs.com/hongzy/p/11519389.html