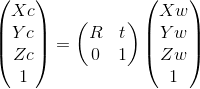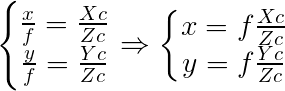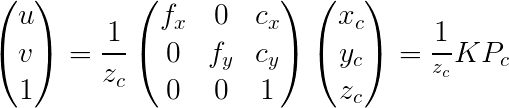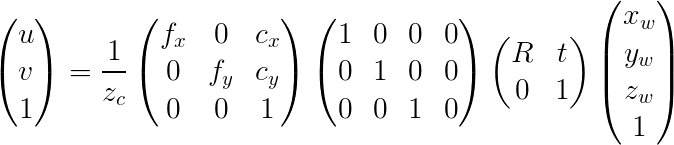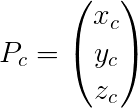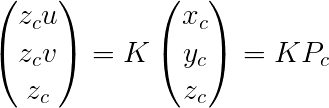为了比较清楚得说明这件事,笔者力求以最简洁的方式进行介绍,
part1:
4个坐标系:
1、世界坐标系(Xw、Yw、Zw)
2、相机坐标系(Xc、Yc、Zc)
3、像平面坐标系(X、Y)
4、像素平面坐标系(u、v)
3个坐标变换关系:
1、世界坐标系(Xw、Yw、Zw)->相机坐标系(Xc、Yc、Zc)
2、相机坐标系(Xc、Yc、Zc)->像平面坐标系(X、Y)
3、像平面坐标系(X、Y)->像素平面坐标系(u、v)
part2:
以下的内容是对上述的7个概念做详细说明:
4个坐标系:
世界坐标系:即自然坐标系
相机坐标系:以相机的的光心为原点,Z轴指向相机前方,x向右,y向下
像平面坐标系:物理成像平面,在距相机光心一倍焦距的平面上(凸透镜成像实验的蜡烛成大小相等倒立的平面)
像素平面坐标系:在距相机光心一个焦距的平面上,原点位于图像的左上角,u轴向右与x轴平行,v轴向下与y轴平行(在凸透镜成像实验的蜡烛成大小相等倒立的距离上放一个屏,相机中的这个位置是一个感光元件)
3个坐标变换关系:
(Xw、Yw、Zw)->(Xc、Yc、Zc):世界坐标系向相机坐标系转换
这俩个坐标系之间的关系我们可以通过旋转矩阵R和平移矩阵t来得到:
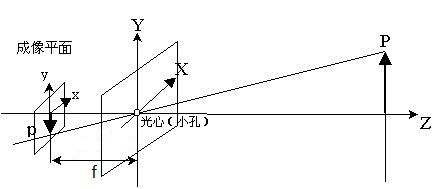
(Xc、Yc、Zc)->(X、Y):相机坐标系向像平面坐标系转换
由以上的介绍,如上图所示,我们知道相机坐标为X-Y-Z,像平面坐标为x-y,由相似三角形关系可知,其中P(Xc,Yc,Zc),p(x,y)
(X、Y)->(u、v):成像平面向像素平面的转换
在相机中,我们很多时候讨论的是基于像素角度的坐标,因为像平面是光学角度,是光在这个平面上的一个成像是个模拟量,所以成像平面需要在成像平面上对像进行采样和量化,这样我们才使得物体的像在像素上的值。像素平面与成像平面之间,相差一个缩放和原点的平移。如下式所示,在u轴上放大了α倍,在v轴上放大β倍,原点平移cx,cy。
好了,到此为止我们已经介绍完了。
part3:
但是,我们还是继续把相关的计算联合起来,给出最后的矩阵形式的表达式。
综合以上相坐标系到成像坐标系及成像坐标系到像素平面坐标系的转换,并把αf合并成fx,把βf合并成fy。
可得相机坐标到像素坐标的计算公式:
这个式子是方程组形式,为显逼格,我们将该式子整理成矩阵形式,其中Pc表示的是点在相机坐标系下的坐标记法:
把世界坐标系到相机坐标系的转换关系也联合起来,进一步可以得到从世界坐标到像素坐标的矩阵形式:
由此,我们已经给出了从世界坐标系到像素坐标系的转换。
part4:
最后,我们聊一聊归一化平面。归一化平面是假想的。
我们知道,当我们用相机坐标时,3D点的表示形式为:
上式可以看出,如果是3D点直接经过内参得到的坐标相当于u,v坐标在各自的方向上都放大了zc倍。
归一化平面是指位于相机前方z=1处的平面上,该平面称为归一化平面。归一化坐标就相当于在z的方向上当z=1时用一个平面截断,这时光心与3D点的连线在该面上的点即为该3d点的归一化点。
表示为,其中Pc1表示的是点在相机坐标系下的坐标记法:
由归一化坐标经过内参之后就得到了相机坐标: