在笔记 4 中,详细阐述了机器学习中利用正则化防止过拟合的基本方法,对 L1 和 L2 范数进行了通俗的解释。为了防止深度神经网络出现过拟合,除了给损失函数加上 L2 正则化项之外,还有一个很著名的方法——dropout.
废话少说,咱们单刀直入正题。究竟啥是 dropout ? dropout 是指在神经网络训练的过程中,对所有神经元按照一定的概率进行消除的处理方式。在训练深度神经网络时,dropout 能够在很大程度上简化神经网络结构,防止神经网络过拟合。所以,从本质上而言,dropout 也是一种神经网络的正则化方法。
假设我们要训练了一个 4 层(3个隐层)的神经网络,该神经网络存在着过拟合。于是我们决定使用 dropout 方法来处理,dropout 为该网络每一层的神经元设定一个失活(drop)概率,在神经网络训练过程中,我们会丢弃一些神经元节点,在网络图上则表示为该神经元节点的进出连线被删除。最后我们会得到一个神经元更少、模型相对简单的神经网络,这样一来原先的过拟合情况就会大大的得到缓解。这样说似乎并没有将 dropout 正则化原理解释清楚,我们继续深究一下:为什么 dropout 可以可以通过正则化发挥防止过拟合的功能?
因为 dropout 可以随时随机的丢弃任何一个神经元,神经网络的训练结果不会依赖于任何一个输入特征,每一个神经元都以这种方式进行传播,并为神经元的所有输入增加一点权重,dropout 通过传播所有权重产生类似于 L2 正则化收缩权重的平方范数的效果,这样的权重压缩类似于 L2 正则化的权值衰减,这种外层的正则化起到了防止过拟合的作用。
所以说,总体而言,dropout 的功能类似于 L2 正则化,但又有所区别。另外需要注意的一点是,对于一个多层的神经网络,我们的 dropout 某层神经元的概率并不是一刀切的。对于不同神经元个数的神经网络层,我们可以设置不同的失活或者保留概率,对于含有较多权值的层,我们可以选择设置较大的失活概率(即较小的保留概率)。所以,总结来说就是如果你担心某些层所含神经元较多或者比其他层更容易发生过拟合,我们可以将该层的失活概率设置的更高一些。
说了这么多,总算大致把 dropout 说明白了。那 dropout 这种操作在实际的 python 编程中该如何实现呢?以一个三层的神经网络为例,首先我们需要定义一个 3 层的 dropout 向量,然后将其与保留概率 keep-prob 进行比较生成一个布尔值向量,再将其与该层的神经元激活输出值进行乘积运算,最后扩展上一步的计算结果,将其除以 keep-prob 即可。但在实际编程中就没说的这么容易了,我们需要对整个神经网络的计算过程进行重新定义,包括前向传播和反向传播的计算定义。
含 dropout 的前向计算定义如下:
defforward_propagation_with_dropout(X, parameters, keep_prob =0.5): np.random.seed(1)# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
D1 = np.random.rand(A1.shape[0], A1.shape[1])
D1 = D1 < keep_prob
A1 = np.multiply(D1, A1)
A1 = A1 / keep_prob
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
D2 = np.random.rand(A2.shape[0], A2.shape[1])
D2 = D2 < keep_prob
A2 = np.multiply(D2, A2)
A2 = A2 / keep_prob
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
returnA3, cache
以上代码基本体现了 dropout 的实现的四步流程。
含 dropout 的反向传播计算定义如下:
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dA2 = np.multiply(dA2, D2)
dA2 = dA2 / keep_prob
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dA1 = np.multiply(dA1, D1)
dA1 = dA1 / keep_prob
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
在定义反向传播计算函数时,我们必须丢弃和执行前向传播时一样的神经元。
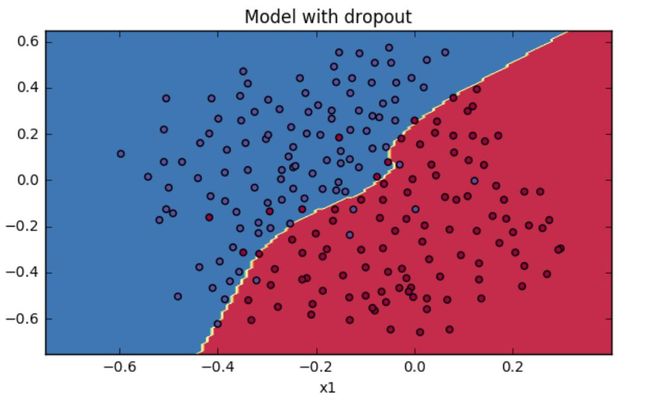
最后带有 dropout 的分类效果如下所示:
所以,总结而言,dropout 就是在正常的神经网络基础上给每一层的每一个神经元加了一道概率流程来随机丢弃某些神经元以达到防止过拟合的目的。