两个基础知识点:递归和时间复杂度
递归
递归函数的特点:自己调用自己,有结束条件,看下面例子:
def fun1(x):
"""无结束条件,报错"""
print(x)
fun1(x-1)
def fun2(x):
"""结束条件为错误条件,报错"""
if x>0:
print(x)
fun2(x+1)
def fun3(x):
"""打印倒序"""
if x>0:
print(x)
fun3(x-1)
def fun4(x):
"""打印正序"""
if x > 0:
fun4(x-1)
print(x)
fun3(7)
fun4(7)结果:
7
6
5
4
3
2
1
*******
1
2
3
4
5
6
7时间复杂度
用来评估算法运行效率的东西:
print('Hello World')
#时间复杂度:O(1)
for i in range(n):
'''时间复杂度:O(n)'''
print('Hello World')
for i in range(n):
'''时间复杂度:O(n^2)'''
for j in range(n):
print('Hello World')
for i in range(n):
'''时间复杂度:O(n^3)'''
for j in range(n):
for k in range(n):
print('Hello World')
while n > 1:
'''时间复杂度:O(log2n)或者O(logn)'''
print(n)
n = n // 2 小结:
- 时间复杂度是用来估算一个算法运行时间的标准
- 一般说来,时间复杂度高的要比时间复杂度低的算法慢
- 常见的复杂度按效率排行:
O(1) < O(logn)
那么如何一样判断时间复杂度?
- 循环减半的过程,O(logn)
- 几次循环就是n的几次方的复杂度
列表查找
- 输入:列表或者待查找元素
- 输出:元素下标或者未查到的元素
顺序查找
从元素的第一个开始,按顺序进行查找,直到找到为止
二分查找
从有序列表的候选区data[0:n]开始,通过对待查找的值与候选区中间值的比较,可以使候选区减少一半。
import time
#定义一个计算运行时间的装饰器
def cal_time(func):
def wrapper(*args,**kwargs):
t1 = time.time()
res = func(*args,**kwargs)
t2 = time.time()
print('%s:%s'%(func.__name__,t2-t1))
return res
return wrapper
#顺序查找
@cal_time
def linear_search(data_set,value):
for i in range(len(data_set)):
if data_set[i] == value:
return i
#二分查找
@cal_time
def bin_search(data_set,value):
low = 0
high = len(data_set) - 1
while low <= high:
mid = (low + high) // 2
if data_set[mid] == value:
return mid
elif data_set[mid] < value:
low = mid + 1
else:
high = mid - 1
ret = linear_search(list(range(100000)),99999)
ret2 = bin_search(list(range(100000)),99999)但有个问题:理论上顺序查找的时间复杂度为O(n),二分查找的为O(logn),看结果二分查找的结果为一个科学记数法,相差2个量级.
linear_search:0.009849071502685547
bin_search:1.5974044799804688e-05列表排序
将无序列表变为有序列表
low逼三人组:冒泡、选择、插入
之前写过:http://www.cnblogs.com/ccorz/p/5581066.html
冒泡
序列中,相邻的两个元素比较大小,如果前面的比后面的元素大,那么交换位置,以此类推...
import random
data = list(range(10000))
random.shuffle(data)
def bubbel_sort(data):
for i in range(len(data) - 1):
for j in range(len(data) - i - 1):
if data[j] > data[j+1]:
data[j], data[j+1] = data[j+1], data[j]
bubbel_sort(data)
print(data)冒泡的优化:
如果排序执行了一趟数据没有交换,那么说明列表已经是有序状态,可以直接结束算法:
def bubbel_sort(data):
for i in range(len(data) - 1):
exchange = False
for j in range(len(data) - i - 1):
if data[j] > data[j+1]:
data[j], data[j+1] = data[j+1], data[j]
exchange = True
if not exchange:
break选择
遍历一趟,选择最小的数放到第一个位置,接着遍历剩下的序列,选择其中最小的,放到剩下序列的第一个位置,如此循环.
import random
data = list(range(1000))
random.shuffle(data)
def select_sort(data):
for i in range(len(data) - 1):
min_loc = i
for j in range(i + 1, len(data)):
if data[j] < data[min_loc]:
min_loc = j
if min_loc != i:
data[i], data[min_loc] = data[min_loc], data[i]
select_sort(data)
print(data)插入排序
列表被分为有序区和无序区两个部分,并且最初有序区只有一个元素.
import random
data = list(range(1000))
random.shuffle(data)
def insert_sort(data):
for i in range(1,len(data)):
tmp = data[i]
j = i - 1
while j >= 0 and data[j] > tmp:
data[j+1] = data[j]
j -= 1
data[j+1] = tmp
insert_sort(data)
print(data)快速排序(简称快排)
好些的算法里最快的,快的排序算法中最好写的。
思路:
- 取第一个元素,是这个元素(P)归位(对的位置)
- 列表被P元素分成两部分
- 递归这两部分列表,以此类推
总结一句话就是:先整理,后递归
import sys, random
#解除python默认递归次数的限制
sys.setrecursionlimit(10000)
data = list(range(1000))
random.shuffle(data)
def quick_sort(data, left, right):
if left < right:
mid = partition(data, left, right)
quick_sort(data, left, mid - 1)
quick_sort(data, mid + 1, right)
def partition(data, left, right):
tmp = data[left]
while left < right:
while left < right and data[right] >= tmp:
right -= 1
data[left] = data[right]
while left < right and data[left] <= tmp:
left += 1
data[right] = data[left]
data[left] = tmp
return left
quick_sort(data, 0, len(data) - 1)
print(data)堆排序
二叉树
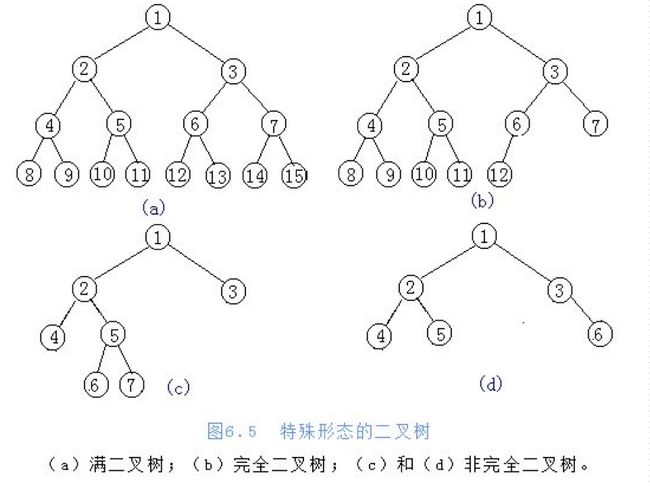
满二叉树是指这样的一种二叉树:除最后一层外,每一层上的所有结点都有两个子结点。在满二叉树中,每一层上的结点数都达到最大值,即在满二叉树的第k层上有2k-1个结点,且深度为m的满二叉树有2m-1个结点。
完全二叉树是指这样的二叉树:除最后一层外,每一层上的结点数均达到最大值;在最后一层上只缺少右边的若干结点。
二叉树的数据存储
二叉树总结
- 二叉树是不超过2个节点的树
- 满二叉树是完全二叉树,完全二叉树不一定是满二叉树
- 完全二叉树可以用列表来存储,通过规律可以从父亲找到孩子,或从孩子找到父亲
堆
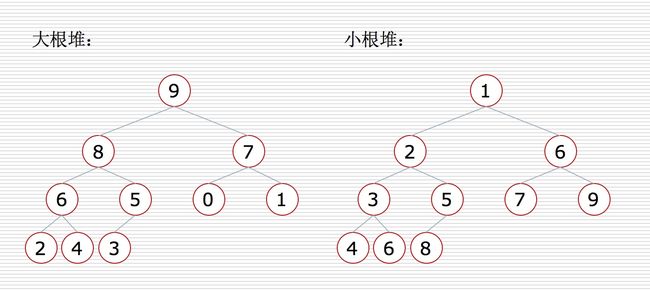
大根堆:一颗完全二叉树,满足任何一节点都比其子节点大
小根堆:一颗完全二叉树,满足任何一节点都比其子节点小
堆排序
堆排序的过程:
- 建立堆
- 得到堆顶元素,假设为最大元素
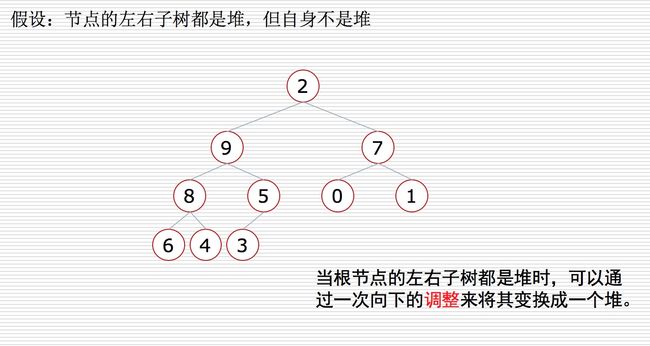
- 去掉堆顶元素,将最后一个元素放到堆顶,此时可以通过一次调整,重新使堆有序
- 堆顶元素为第二大元素
- 重复步骤三
代码:
import sys, random
sys.setrecursionlimit(10000)
data = list(range(100))
random.shuffle(data)
def sift(data,low,high):
'''堆整理,选出最大的元素'''
i = low
j = 2*i+1
k = j +1
tmp = data[i]
while j <= high:
if j < high and data[j] < data[k]:
j+=1
if tmp < data[j]:
data[i]=data[j]
i=j
j=2*i+1
else:
break
data[i]=tmp
def heap_sort(data):
n = len(data)
for i in range(n//2-1,-1,-1):
sift(data,i,n-1)
for i in range(n-1,-1,-1):
data[0],data[i]=data[i],data[0]
sift(data,0,i-1)
heap_sort(data)
print(data)out:
[0, 1, 2, 3, 12, 5, 4, 6, 7, 8, 25, 9, 10, 11, 17, 23, 13, 73, 29, 14, 15, 19, 40, 28, 44, 64, 30, 27, 18, 16, 21, 70, 22, 20, 31, 24, 34, 32, 33, 26, 35, 36, 39, 46, 37, 41, 38, 42, 86, 45, 43, 51, 62, 47, 49, 75, 72, 54, 50, 48, 57, 63, 68, 56, 87, 60, 67, 59, 55, 78, 58, 61, 69, 52, 53, 80, 83, 65, 89, 66, 94, 91, 71, 82, 92, 90, 77, 81, 74, 84, 95, 76, 85, 88, 93, 79, 96, 98, 97, 99]