RGB-D直接法
RGB-D直接法有下列分类:
- 感兴趣的P来自于稀疏关键点,通常一幅图像使用数百个到上千个特征点,这些特征点检测出来会耗费一定的时间,但是不计算描述子,而且使用的像素点很少,因此速度很快,可以在CPU上运行,但如果图像变化过于剧烈就会出现大概率丢失特征点的问题
- 感兴趣的P来自于所有有图像梯度的像素点,也就是是图像里的边界,由于像素梯度为0不会对估计造成任何影响,所以可以只考虑梯度明显的地方放弃梯度不明显的地方,这称为Semi-Dense直接法,可以重构一个半稠密结构
- 感兴趣的P来自于整副图像,由于计算资源消耗太大,不能够在CPU上运行
稀疏直接法的实验
数据部分介绍
同样是TUM数据集(9张对齐的深度图和彩色图,以及对齐的信息)
Cpp
#include
#include CMakeLists.txt
cmake_minimum_required( VERSION 2.8 )
project( directMethod )
set( CMAKE_BUILD_TYPE Release )
set( CMAKE_CXX_FLAGS "-std=c++11 -O3" )
# 添加cmake模块路径
list( APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake_modules )
find_package( OpenCV )
include_directories( ${OpenCV_INCLUDE_DIRS} )
find_package( G2O )
include_directories( ${G2O_INCLUDE_DIRS} )
include_directories( "/usr/include/eigen3" )
set( G2O_LIBS
g2o_core g2o_types_sba g2o_solver_csparse g2o_stuff g2o_csparse_extension
)
add_executable( direct_sparse direct_sparse.cpp )
target_link_libraries( direct_sparse ${OpenCV_LIBS} ${G2O_LIBS} )
add_executable( direct_semidense direct_semidense.cpp )
target_link_libraries( direct_semidense ${OpenCV_LIBS} ${G2O_LIBS} )
Bash指令:
cd code/slambook/ch8/directMethod
mkdir build
cd build
cmake ..
make
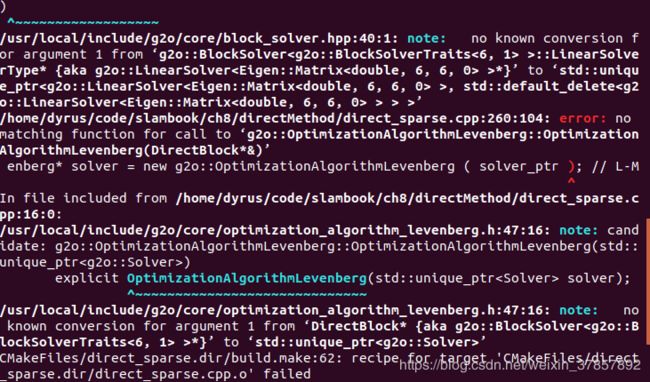
/*
// 初始化g2o
typedef g2o::BlockSolver> DirectBlock; // 求解的向量是6*1的
DirectBlock::LinearSolverType* linearSolver = new g2o::LinearSolverDense< DirectBlock::PoseMatrixType > ();
DirectBlock* solver_ptr = new DirectBlock ( linearSolver );
// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr ); // G-N
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr ); // L-M
*/
typedef g2o::BlockSolver<g2o::BlockSolverTraits<6,1>> DirectBlock; // 求解的向量是6*1的
std::unique_ptr<DirectBlock::LinearSolverType> linearSolver ( new g2o::LinearSolverDense<DirectBlock::PoseMatrixType>());
std::unique_ptr<DirectBlock> solver_ptr ( new DirectBlock ( std::move(linearSolver)));
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( std::move(solver_ptr));
./direct_sparse ../../data

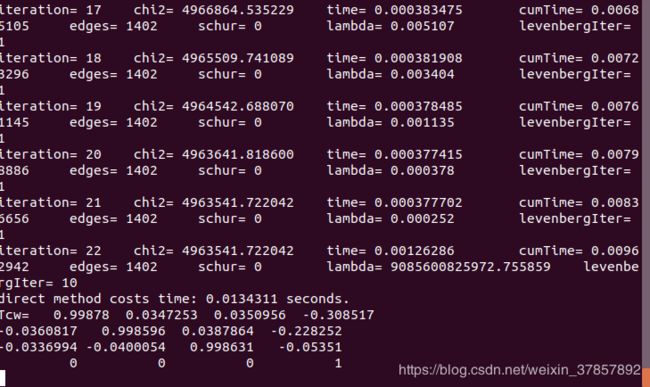
上方是迭代过程,下方是估计出来的T矩阵,使用的优化器是LM算法
半稠密直接法的实验
数据类型和算法都与稀疏直接法一样,所不同的只是我们感兴趣的P点,对P点选取算法更改如下:
// select the pixels with high gradiants
for ( int x=10; x<gray.cols-10; x++ )
for ( int y=10; y<gray.rows-10; y++ )
{
Eigen::Vector2d delta (
gray.ptr<uchar>(y)[x+1] - gray.ptr<uchar>(y)[x-1],
gray.ptr<uchar>(y+1)[x] - gray.ptr<uchar>(y-1)[x]
);
if ( delta.norm() < 50 )
continue;
ushort d = depth.ptr<ushort> (y)[x];
if ( d==0 )
continue;
Eigen::Vector3d p3d = project2Dto3D ( x, y, d, fx, fy, cx, cy, depth_scale );
float grayscale = float ( gray.ptr<uchar> (y) [x] );
measurements.push_back ( Measurement ( p3d, grayscale ) );
}
同样修正编译错误:
/*
// 初始化g2o
typedef g2o::BlockSolver> DirectBlock; // 求解的向量是6*1的
DirectBlock::LinearSolverType* linearSolver = new g2o::LinearSolverDense< DirectBlock::PoseMatrixType > ();
DirectBlock* solver_ptr = new DirectBlock ( linearSolver );
// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr ); // G-N
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr ); // L-M
*/
typedef g2o::BlockSolver<g2o::BlockSolverTraits<6,1>> DirectBlock; // 求解的向量是6*1的
std::unique_ptr<DirectBlock::LinearSolverType> linearSolver ( new g2o::LinearSolverDense<DirectBlock::PoseMatrixType>());
std::unique_ptr<DirectBlock> solver_ptr ( new DirectBlock ( std::move(linearSolver)));
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( std::move(solver_ptr));
Bash执行:
./direct_semidense ../../data

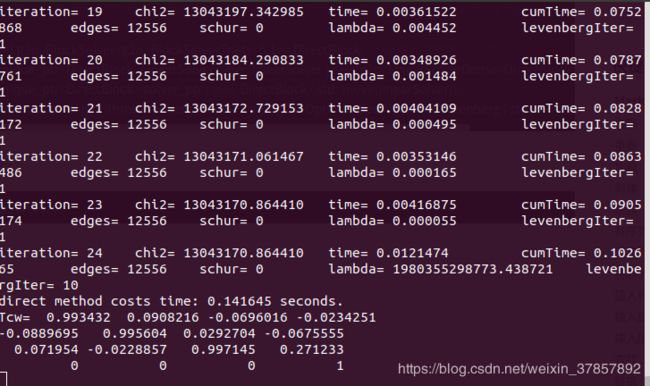
可以比较一下稀疏直接法和半稠密直接法的估计时间,13ms和141ms,对应76帧和7帧,正常实时的在线估计要求在60帧左右,所以如果用一般的CPU去计算,半稠密直接法无法用于实时估计
讨论
实际的图像往往具有很强的非凸性,利用梯度下降原理的凸优化算法往往达不到全局最小值。有时会使用小的图像块patch去做整体梯度,并且使用更加复杂的差异度量方法,比如说归一化相关性NCC
优点:
1.省去计算特征点和描述子的计算时间
2.只需要梯度,不需要特征点,可以在特征缺失的场景下使用
3.可以构建稠密地图
缺点:
1.非凸性容易导致局部最优
2.单个像素没有区分度
3.灰度值不变是很强的假设,需要使用更细致的光度模型标定相机