Apriori算法原理总结

转载

---

Aprior算法是常用的用于挖掘出数据关联规则的算法，它用来找出数据值中频繁出现的数据集合，找出这些集合的模式有助于我们做一些决策。比如在常见的超市购物数据集，或者电商的网购数据集中，如果我们找到了频繁出现的数据集，那么对于超市，我们可以优化产品的位置摆放，对于电商，我们可以优化商品所在的仓库位置，达到节约成本，增加经济效益的目的。下面我们就对Apriori算法做一个总结。

---

1.频繁项集的评估标准

什么样的数据才是频繁项集呢？也许你会说，这还不简单，肉眼一扫，一起出现次数多的数据集就是频繁项集吗！的确，这也没有说错，但是有两个问题，第一是当数据量非常大的时候，我们没法直接肉眼发现频繁项集，这催生了关联规则挖掘的算法，比如Apriori, PrefixSpan, CBA。第二是我们缺乏一个频繁项集的标准。比如10条记录，里面A和B同时出现了三次，那么我们能不能说A和B一起构成频繁项集呢？因此我们需要一个评估频繁项集的标准。

常用的频繁项集的评估标准有支持度、置信度和提升度三个。

支持度就是几个关联的数据在数据集中出现的次数占总数据集的比重。或者说几个数据关联出现的概率。如果我们有两个想分析关联性的数据X和Y，则对应的支持度为：$$Support(X,Y)=P(XY)=\frac{number(XY)}{number(AllSamples)}$$
以此类推，如果我们有三个想分析关联性的数据X，Y和Z，则对应的支持度为：$$Support(X,Y,Z)=P(XYZ)=\frac{number(XYZ)}{number(AllSamples)}$$
一般来说，支持度高的数据不一定构成频繁项集，但是支持度太低的数据肯定不构成频繁项集。

置信度体现了一个数据出现后，另一个数据出现的概率，或者说数据的条件概率。如果有两个想分析关联性的数据X和Y，X对Y的置信度为：$$Confidence(X\Leftarrow Y)=P(X\mid Y)=\frac{P(XY)}{P(Y)}$$
也可以以此类推到多个数据的关联置信度，比如对于三个数据X，Y，Z，则X对于Y和Z的置信度为：$$Confidence(X\Leftarrow YZ)=P(X\mid YZ)=\frac{P(XYZ)}{P(YZ)}$$
举个例子，在购物数据中，纸巾对应鸡爪的置信度为40%，支持度为1%。则意味着在购物数据中，总共有1%的用户既买鸡爪又买纸巾;同时买鸡爪的用户中有40%的用户购买纸巾。

提升度表示含有Y的条件下，同时含有X的概率，与X总体发生的概率之比，即：
$$Lift(X\Leftarrow Y)=\frac{P(X\mid Y)}{P(X)}=\frac{Confidence(X\Leftarrow Y)}{P(X)}$$
提升度体现了X和Y之间的关联关系，提升度大于1则 $X\Leftarrow Y$是有效的强关联规则。一个特殊情况，如果X和Y独立，则有 $Lift(X\Leftarrow Y)=1$，因为此时 $P(X\mid Y)=P(X)$.

一般来说，要选择一个数据集合中的频繁数据集，则需要自定义评估标准。最常用的评估标准是用自定义的支持度，或者是自定义支持度和置信度的一个组合。

2.Apriori算法思想

对于Apriori算法，我们使用支持度来作为我们判断频繁项集的标准。Apriori算法的目标是找到最大的K项频繁集。这里有两层意思，首先，我们要找到符合支持度标准的频繁集。但是这样的频繁集可能有很多。第二层意思就是我们要找到最大个数的频繁集。比如我们找到符合支持度的频繁集AB和ABE，那么我们会抛弃AB，只保留ABE，因为AB是2项频繁集，而ABE是3项频繁集。那么具体的，Apriori算法是如何做到挖掘K项频繁集的呢？
　
Apriori算法采用了迭代的方法，先搜索出候选1项集及对应的支持度，剪枝去掉低于支持度的1项集，得到频繁1项集。然后对剩下的频繁1项集进行连接，得到候选的频繁2项集，筛选去掉低于支持度的候选频繁2项集，得到真正的频繁二项集，以此类推，迭代下去，直到无法找到频繁k+1项集为止，对应的频繁k项集的集合即为算法的输出结果。

可见这个算法还是很简洁的，第i次的迭代过程包括扫描计算候选频繁i项集的支持度，剪枝得到真正频繁i项集和连接生成候选频繁i+1项集三步。

我们下面这个简单的例子看看：

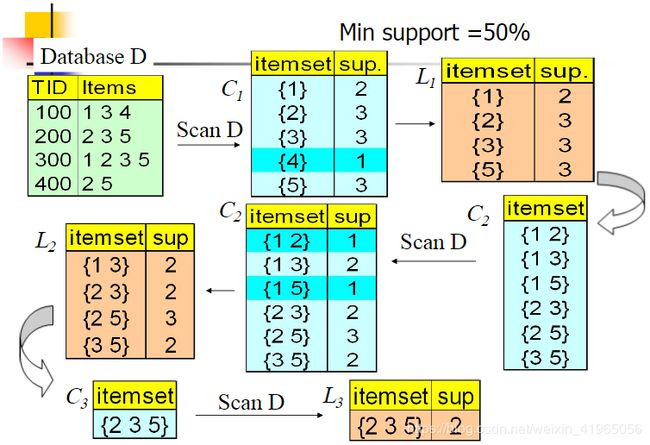
我们的数据集D有4条记录，分别是134,235,1235和25。现在我们用Apriori算法来寻找频繁k项集，最小支持度设置为50%。首先我们生成候选频繁1项集，包括我们所有的5个数据并计算5个数据的支持度，计算完毕后我们进行剪枝，数据4由于支持度只有25%被剪掉。我们最终的频繁1项集为1235，现在我们链接生成候选频繁2项集，包括12,13,15,23,25,35共6组。此时我们的第一轮迭代结束。

进入第二轮迭代，我们扫描数据集计算候选频繁2项集的支持度，接着进行剪枝，由于12和15的支持度只有25%而被筛除，得到真正的频繁2项集，包括13,23,25,35。现在我们链接生成候选频繁3项集,123, 125，135和235共4组，这部分图中没有画出。通过计算候选频繁3项集的支持度，我们发现123,125和135的支持度均为25%，因此接着被剪枝，最终得到的真正频繁3项集为235一组。由于此时我们无法再进行数据连接，进而得到候选频繁4项集，最终的结果即为频繁3三项集235。

3.算法流程

下面我们对Aprior算法流程做一个总结。

输入：数据集合D，支持度阈值α
输出：最大的频繁k项集

• 扫描整个数据集，得到所有出现过的数据，作为候选频繁1项集。k=1，频繁0项集为空集
• 挖掘频繁k项集
  • 扫描数据计算候选频繁k项集的支持度
  • 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集为空，则直接返回频繁k-1项集的集合作为算法结果，算法结束。如果得到的频繁k项集只有一项，则直接返回频繁k项集的集合作为算法结果，算法结束。
  • 基于频繁k项集，连接生成候选频繁k+1项集。
• 令k=k+1，转入步骤2。

从算法的步骤可以看出，Aprior算法每轮迭代都要扫描数据集，因此在数据集很大，数据种类很多的时候，算法效率很低。

4. Aprior算法总结

Aprior算法是一个非常经典的频繁项集的挖掘算法，很多算法都是基于Aprior算法而产生的，包括FP-Tree,GSP, CBA等。这些算法利用了Aprior算法的思想，但是对算法做了改进，数据挖掘效率更好一些，因此现在一般很少直接用Aprior算法来挖掘数据了，但是理解Aprior算法是理解其它Aprior类算法的前提，同时算法本身也不复杂，因此值得好好研究一番。

不过scikit-learn中并没有频繁集挖掘相关的算法类库，这不得不说是一个遗憾，不知道后面的版本会不会加上。

5. Python实现

class Apriori:

    @classmethod
    def caculate(cls, dataSet, minSupport=0.5):
        C1 = cls.createC1(dataSet)
        # 将dataSet集合化，以满足scanD的格式要求
        # D = map(set, dataSet)
        L1, supportData = cls.scanD(dataSet, C1, minSupport)
        L = [L1]
         # 最初的L1中的每个项集含有一个元素，新生成的
         # 项集应该含有2个元素，所以 k=2
        k = 2
        while (len(L[k - 2]) > 0):
            Ck = cls.aprioriGen(L[k - 2], k)
            Lk, supK = cls.scanD(dataSet, Ck, minSupport)
            # 将新的项集的支持度数据加入原来的总支持度字典中
            supportData.update(supK)
            # 将符合最小支持度要求的项集加入L
            L.append(Lk)
            # 新生成的项集中的元素个数应不断增加
            k += 1
        # 返回所有满足条件的频繁项集的列表，和所有候选项集的支持度信息
        return L, supportData

    @classmethod
    def createC1(self, dataSet):
     '''
    构建初始候选项集的列表，即所有候选项集只包含一个元素，
    C1是大小为1的所有候选项集的集合
    '''
        C1 = []
        for transaction in dataSet:
            for item in transaction:
                if not [item] in C1:
                    C1.append([item])
        C1.sort()
        return map(frozenset, C1)

    @classmethod
    def aprioriGen(cls, Lk, k):
     '''
    由初始候选项集的集合Lk生成新的生成候选项集，
    k表示生成的新项集中所含有的元素个数
    '''
        retList = []
        lenLk = len(Lk)
        for i in range(lenLk):
            for j in range(i + 1, lenLk):
                L1 = list(Lk[i])[: k - 2]
                L2 = list(Lk[j])[: k - 2]
                L1.sort()
                L2.sort()
                if L1 == L2:
                    retList.append(Lk[i] | Lk[j])
        return retList

    @classmethod
    def scanD(self, D, Ck, minSupport):
     '''
    计算Ck中的项集在数据集合D(记录或者transactions)中的支持度,
    返回满足最小支持度的项集的集合，和所有项集支持度信息的字典。
    '''
        ssCnt = {}
        l_Ck = list(Ck)
        for tid in D:
        # 对于每一条transaction
            for can in l_Ck:
            # 对于每一个候选项集can，检查是否是transaction的一部分
            # 即该候选can是否得到transaction的支持
                if can.issubset(tid):
                    if ssCnt.get(can) == None: ssCnt[can] = 1
                    else: ssCnt[can] += 1
        numItems = float(len(D))
        retList = []
        supportData = {}
        for key in ssCnt:
        # 每个项集的支持度
            support = ssCnt[key]/numItems
            # 将满足最小支持度的项集，加入retList
            if support >= minSupport:
                retList.insert(0, key)
            else:
                #print(str(key) + "支持度：" + str(support)+ "，小于最小支持度：" + str(minSupport))
                pass
            # 汇总支持度数据
            supportData[key] = support
        return retList, supportData