Python之探索式数据分析

探究数据分析的目的是为了找到有助于清理/准备/转换数据的思路，这些数据最终将用于机器学习算法/模型的建立。我们将采取以下行动：

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

plt.style.use('bmh')

Seaborn是一个基于matplotlib的Python数据可视化库。它提供了一个绘制信息统计图形的高级界面。

即使是漂亮的图表bokeh。

考虑住房价格及其影响因素。

data = pd.read_csv('data/train.csv')
data.head()

以上为部分数据截图

data.info()

RangeIndex: 1460 entries, 0 to 1459
Data columns (total 81 columns):
Id               1460 non-null int64
MSSubClass       1460 non-null int64
MSZoning         1460 non-null object
LotFrontage      1201 non-null float64
LotArea          1460 non-null int64
Street           1460 non-null object
Alley            91 non-null object
LotShape         1460 non-null object
LandContour      1460 non-null object
Utilities        1460 non-null object
LotConfig        1460 non-null object
LandSlope        1460 non-null object
Neighborhood     1460 non-null object
Condition1       1460 non-null object
Condition2       1460 non-null object
BldgType         1460 non-null object
HouseStyle       1460 non-null object
OverallQual      1460 non-null int64
OverallCond      1460 non-null int64
YearBuilt        1460 non-null int64
YearRemodAdd     1460 non-null int64
RoofStyle        1460 non-null object
RoofMatl         1460 non-null object
Exterior1st      1460 non-null object
Exterior2nd      1460 non-null object
MasVnrType       1452 non-null object
MasVnrArea       1452 non-null float64
ExterQual        1460 non-null object
ExterCond        1460 non-null object
Foundation       1460 non-null object
BsmtQual         1423 non-null object
BsmtCond         1423 non-null object
BsmtExposure     1422 non-null object
BsmtFinType1     1423 non-null object
BsmtFinSF1       1460 non-null int64
BsmtFinType2     1422 non-null object
BsmtFinSF2       1460 non-null int64
BsmtUnfSF        1460 non-null int64
TotalBsmtSF      1460 non-null int64
Heating          1460 non-null object
HeatingQC        1460 non-null object
CentralAir       1460 non-null object
Electrical       1459 non-null object
1stFlrSF         1460 non-null int64
2ndFlrSF         1460 non-null int64
LowQualFinSF     1460 non-null int64
GrLivArea        1460 non-null int64
BsmtFullBath     1460 non-null int64
BsmtHalfBath     1460 non-null int64
FullBath         1460 non-null int64
HalfBath         1460 non-null int64
BedroomAbvGr     1460 non-null int64
KitchenAbvGr     1460 non-null int64
KitchenQual      1460 non-null object
TotRmsAbvGrd     1460 non-null int64
Functional       1460 non-null object
Fireplaces       1460 non-null int64
FireplaceQu      770 non-null object
GarageType       1379 non-null object
GarageYrBlt      1379 non-null float64
GarageFinish     1379 non-null object
GarageCars       1460 non-null int64
GarageArea       1460 non-null int64
GarageQual       1379 non-null object
GarageCond       1379 non-null object
PavedDrive       1460 non-null object
WoodDeckSF       1460 non-null int64
OpenPorchSF      1460 non-null int64
EnclosedPorch    1460 non-null int64
3SsnPorch        1460 non-null int64
ScreenPorch      1460 non-null int64
PoolArea         1460 non-null int64
PoolQC           7 non-null object
Fence            281 non-null object
MiscFeature      54 non-null object
MiscVal          1460 non-null int64
MoSold           1460 non-null int64
YrSold           1460 non-null int64
SaleType         1460 non-null object
SaleCondition    1460 non-null object
SalePrice        1460 non-null int64
dtypes: float64(3), int64(35), object(43)
memory usage: 924.0+ KB

从这些信息中我们已经可以看出，有些数据将与我们的目的无关，因为它包含了太多的NaN值（Drummer、Alley和PoolQC）。此外，即使没有这些数据，表中也有足够的证据进行分析，所以我们可能不会考虑其中的一些数据。让我们去掉变量Id和含有30%以上NaN值的变量。

# pandas.DataFrame.count() does not include NaN values
data_without_nan = data[[column for column in data if data[column].count() / len(data) >= 0.3]]
data_without_nan = data_without_nan.drop(columns=['Id'])

dropped_columns = [col for col in data.columns if col not in data_without_nan.columns ]
print("List of dropped columns: ", dropped_columns)

现在我们来看看房价的分布情况。

data_without_nan['SalePrice'].describe()

# histogram and normal probability plot
from scipy import stats
from scipy.stats import norm

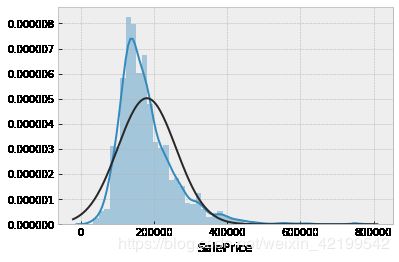
sns.distplot(data_without_nan['SalePrice'], fit=norm);
fig = plt.figure()
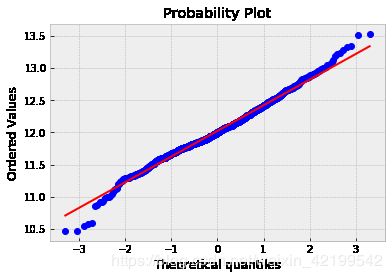
res = stats.probplot(data_without_nan['SalePrice'], plot=plt)

 

我们可以看到，价格是向右倾斜的，而且有一些排放量在~500000以上。最终，我们将需要摆脱它们，以获得自变量（'SalePrice'）的正态分布。

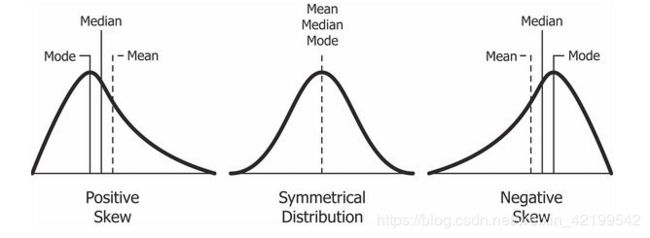
右斜分布有一个长长的右尾。右斜分布也叫正斜分布，因为数值线上有一个正方向的长尾。均值和中位数也是在峰值的右侧。

在偏移量为正值的情况下，数据的对数化效果非常好。

此外，你还可以使用Box-Cox转换。

# transformed histogram and normal probability plot
sns.distplot(np.log(data_without_nan['SalePrice']), fit=norm);
fig = plt.figure()
res = stats.probplot(np.log(data_without_nan['SalePrice']), plot=plt)

我们来看看其他星座的分布情况。要做到这一点，您必须首先只选择数字数据。

list(set(data_without_nan.dtypes.tolist()))

data_without_nan_num = data_without_nan.select_dtypes(include = ['float64', 'int64'])
data_without_nan_num.head()

以下为部分结果截图

现在让我们把它们都建起来。

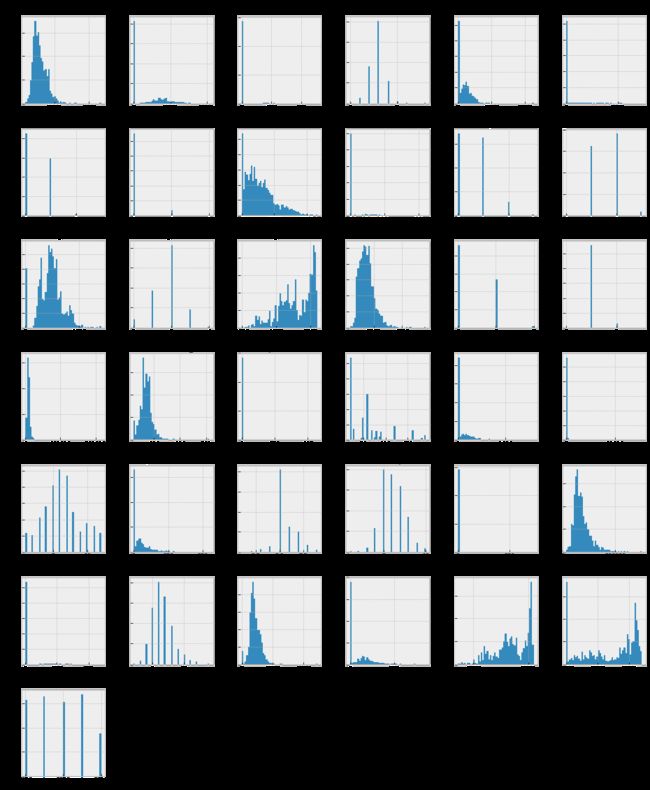
data_without_nan_num.hist(figsize=(16, 20), bins=50, xlabelsize=8, ylabelsize=8); 
# ; avoid having the matplotlib verbose informations

如 "1stFlrSF"、"TotalBsmtSF"、"LotFrontage"、"GrLiveArea "等功能......。图形上与 "SalePrice "变量的分布相似。

相关性

让我们试着找到与 "SalePrice "相关的标志。

corr_data = data_without_nan_num.corr()['SalePrice'][:-1]
correlated_features_list = corr_data[abs(corr_data) > 0.5].sort_values(ascending=False)
print("There are {} strongly correlated values with SalePrice:\n{}".format(len(correlated_features_list), 
                                                                          correlated_features_list))

现在，我们有了一份与住房成本相关的变量清单，但这份清单并不完整，因为我们知道，这种相关性取决于排放量。因此，我们可以进行如下操作：

得到一张数字特征图，看看哪些人的排放很少或解释的排放。
删去排放，重新计算相关。
顺便说一下，相关性本身不一定能解释数据之间的关系。例如，比线性关系更复杂的关系，就不能简单地看关联度的值来猜测。所以，我们也来看看我们从关联表中排除的征兆，并建立它们，看看它们和房价之间是否有关联性。

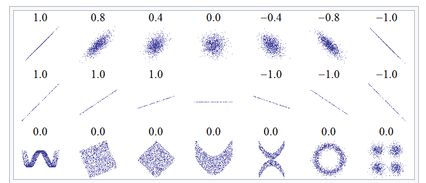
考虑下图中的许多相关领域（Correlation）。值的分布(,)，每一个值都有相应的相关系数。相关系数反映了线性依赖关系的 "噪声"（上线），但不能描述线性依赖关系的斜率（中线），完全不适合描述复杂的非线性依赖关系（下线）。对于图中所示的分布，由于离散度y为零，所以没有定义相关系数。

for i in range(0, len(data_without_nan_num.columns), 5):
    sns.pairplot(data=data_without_nan_num,
                x_vars=data_without_nan_num.columns[i:i+5],
                y_vars=['SalePrice'])

 

我们可以清楚地发现这些迹象之间的一些联系。它们中的大多数似乎与 "SalePrice "有线性联系，如果你仔细观察数据，你会发现许多数据点位于x=0，这可能表明在特定的房屋中没有这样的调查特征（例如，"OpenPorchSF"--存在一个开放的门廊）。

我们试着把这些0从数值中去掉，重复寻找与房价最相关的数值。

import operator

individual_features_df = []
for i in range(0, len(data_without_nan_num.columns) - 1): # -1 because the last column is SalePrice
    tmp_data = data_without_nan_num[[data_without_nan_num.columns[i], 'SalePrice']]
    tmp_data = tmp_data[tmp_data[data_without_nan_num.columns[i]] != 0]
    individual_features_df.append(tmp_data)

all_correlations = {feature.columns[0]: feature.corr()['SalePrice'][0] for feature in individual_features_df}
all_correlations = sorted(all_correlations.items(), key=operator.itemgetter(1))
for (key, value) in all_correlations:
    print("{:>15}: {:>15}".format(key, value))

还有一个与 "SalePrice "相关的标志--"2ndFlrSF"。
 

correlated_features_list = [key for key, value in all_correlations if abs(value) >= 0.5]
print("There is {} strongly correlated values with SalePrice:\n{}".format(len(correlated_features_list), 
                                                                          correlated_features_list))

因此，有11个预测因素与 "SalePrice "相关。

我们还可以为我们暂时排除在考虑范围之外的分类特征引入额外的虚拟变量。

符号'2ndFlrSF'（有很多零）也可以通过标记1它的存在使其分类，数值可以加到变量'1stFlrSF'中。

data_without_nan_num[['1stFlrSF', '2ndFlrSF']]

1stFlrSF	2ndFlrSF
0	856	854
1	1262	0
2	920	866
3	961	756
4	1145	1053
5	796	566
6	1694	0
7	1107	983
8	1022	752
9	1077	0
10	1040	0
11	1182	1142
12	912	0
13	1494	0
14	1253	0
15	854	0
16	1004	0
17	1296	0
18	1114	0
19	1339	0
20	1158	1218
21	1108	0
22	1795	0
23	1060	0
24	1060	0
25	1600	0
26	900	0
27	1704	0
28	1600	0
29	520	0
...	...	...
1430	734	1104
1431	958	0
1432	968	0
1433	962	830
1434	1126	0
1435	1537	0
1436	864	0
1437	1932	0
1438	1236	0
1439	1040	685
1440	1423	748
1441	848	0
1442	1026	981
1443	952	0
1444	1422	0
1445	913	0
1446	1188	0
1447	1220	870
1448	796	550
1449	630	0
1450	896	896
1451	1578	0
1452	1072	0
1453	1140	0
1454	1221	0
1455	953	694
1456	2073	0
1457	1188	1152
1458	1078	0
1459	1256	0

1460 rows × 2 columns

特征与特征间的关系

让我们看看变量之间的关系，而不是与 "SalePrice "的关系。

corr = data_without_nan_num.drop('SalePrice', axis=1).corr() # We've already examined SalePrice correlations
plt.figure(figsize=(12, 10))

sns.heatmap(corr[(corr >= 0.5) | (corr <= -0.4)], 
            cmap='viridis', vmax=1.0, vmin=-1.0, linewidths=0.1,
            annot=True, annot_kws={"size": 8}, square=True);

很多因素是相互关联的。

一些因素，如YearBuild/GarageYrBlt，可能只是表明一段时间内的价格上涨。至于1stFlrSF/TotalBsmtSF这一对的相关性，似乎符合逻辑，1楼越大（考虑到很多房子只有1楼），普通的地下室就越大。这对于GarageCars/GarageArea对来说也是一样的。

因此，对于强相关的特征(1FlrSF/TotalBsmtSF，GarageCars/GarageArea)，只包含其中的一对是有意义的。

Q -> Q (Quantitative to Quantitative relationship)

除了按数据类型选择外，还可以查看数据描述（如果有的话），并选择严格的定量特征来查看数据和因变量之间的关系。
 

quantitative_features_list = ['LotFrontage', 'LotArea', 'MasVnrArea', 'BsmtFinSF1', 'BsmtFinSF2', 'TotalBsmtSF', '1stFlrSF',
    '2ndFlrSF', 'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath',
    'BedroomAbvGr', 'KitchenAbvGr', 'TotRmsAbvGrd', 'Fireplaces', 'GarageCars', 'GarageArea', 'WoodDeckSF', 'OpenPorchSF', 
    'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'MiscVal', 'SalePrice']
df_quantitative_values = data_without_nan[quantitative_features_list]
df_quantitative_values.head()

LotFrontage	LotArea	MasVnrArea	BsmtFinSF1	BsmtFinSF2	TotalBsmtSF	1stFlrSF	2ndFlrSF	LowQualFinSF	GrLivArea	...	GarageCars	GarageArea	WoodDeckSF	OpenPorchSF	EnclosedPorch	3SsnPorch	ScreenPorch	PoolArea	MiscVal	SalePrice
0	65.0	8450	196.0	706	0	856	856	854	0	1710	...	2	548	0	61	0	0	0	0	0	208500
1	80.0	9600	0.0	978	0	1262	1262	0	0	1262	...	2	460	298	0	0	0	0	0	0	181500
2	68.0	11250	162.0	486	0	920	920	866	0	1786	...	2	608	0	42	0	0	0	0	0	223500
3	60.0	9550	0.0	216	0	756	961	756	0	1717	...	3	642	0	35	272	0	0	0	0	140000
4	84.0	14260	350.0	655	0	1145	1145	1053	0	2198	...	3	836	192	84	0	0	0	0	0	250000

5 rows × 28 columns

让我们挑出与房价相关性最大的因素。

features_to_analyse = [x for x in quantitative_features_list if x in correlated_features_list]
features_to_analyse.append('SalePrice')
features_to_analyse

我们来看看所选数据的回归图。

fig, ax = plt.subplots(round(len(features_to_analyse) / 3), 3, figsize = (18, 12))

for i, ax in enumerate(fig.axes):
    if i < len(features_to_analyse) - 1:
        sns.regplot(x=features_to_analyse[i], y='SalePrice', data=data_without_nan[features_to_analyse], ax=ax)

TotalBsmtSF、1stFlrSF（之前我们已经决定用2ndFlrSF进行总结，并为2ndFlrSF进入类别变量）、GrLivArea和GarageArea适合在定量变量中建立模型。

C -> Q (Categorical to Quantitative relationship)

让我们来看看断然的特征。

# quantitative_features_list[:-1] as the last column is SalePrice and we want to keep it
categorical_features = [a for a in quantitative_features_list[:-1] + 
                        data_without_nan.columns.tolist() if (a not in quantitative_features_list[:-1]) or 
                        (a not in data_without_nan.columns.tolist())]
df_categ = data_without_nan[categorical_features]
df_categ.head()

MSSubClass	MSZoning	Street	LotShape	LandContour	Utilities	LotConfig	LandSlope	Neighborhood	Condition1	...	GarageYrBlt	GarageFinish	GarageQual	GarageCond	PavedDrive	MoSold	YrSold	SaleType	SaleCondition	SalePrice
0	60	RL	Pave	Reg	Lvl	AllPub	Inside	Gtl	CollgCr	Norm	...	2003.0	RFn	TA	TA	Y	2	2008	WD	Normal	208500
1	20	RL	Pave	Reg	Lvl	AllPub	FR2	Gtl	Veenker	Feedr	...	1976.0	RFn	TA	TA	Y	5	2007	WD	Normal	181500
2	60	RL	Pave	IR1	Lvl	AllPub	Inside	Gtl	CollgCr	Norm	...	2001.0	RFn	TA	TA	Y	9	2008	WD	Normal	223500
3	70	RL	Pave	IR1	Lvl	AllPub	Corner	Gtl	Crawfor	Norm	...	1998.0	Unf	TA	TA	Y	2	2006	WD	Abnorml	140000
4	60	RL	Pave	IR1	Lvl	AllPub	FR2	Gtl	NoRidge	Norm	...	2000.0	RFn	TA	TA	Y	12	2008	WD	Normal	250000

5 rows × 49 columns

df_not_num = df_categ.select_dtypes(include = ['O'])
print('There is {} non numerical features including:\n{}'.format(len(df_not_num.columns), df_not_num.columns.tolist()))

让我们来看看特征

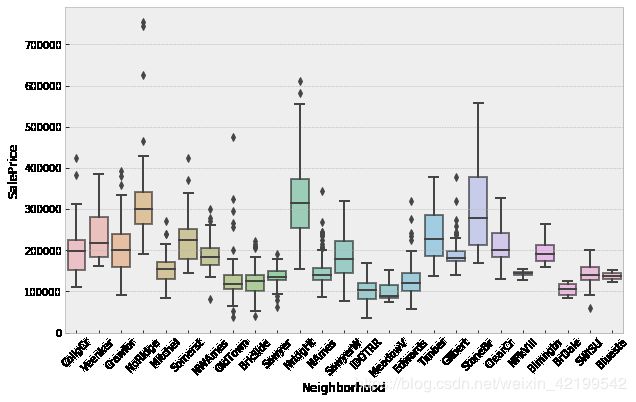
plt.figure(figsize = (10, 6))
ax = sns.boxplot(x='Neighborhood', y='SalePrice', data=df_categ)
plt.setp(ax.artists, alpha=.5, linewidth=2, edgecolor="k")
plt.xticks(rotation=45)

plt.figure(figsize = (12, 6))
ax = sns.boxplot(x='HouseStyle', y='SalePrice', data=df_categ)
plt.setp(ax.artists, alpha=.5, linewidth=2, edgecolor="k")
plt.xticks(rotation=45)

(array([0, 1, 2, 3, 4, 5, 6, 7]), )

让我们来看看它们的分布情况。

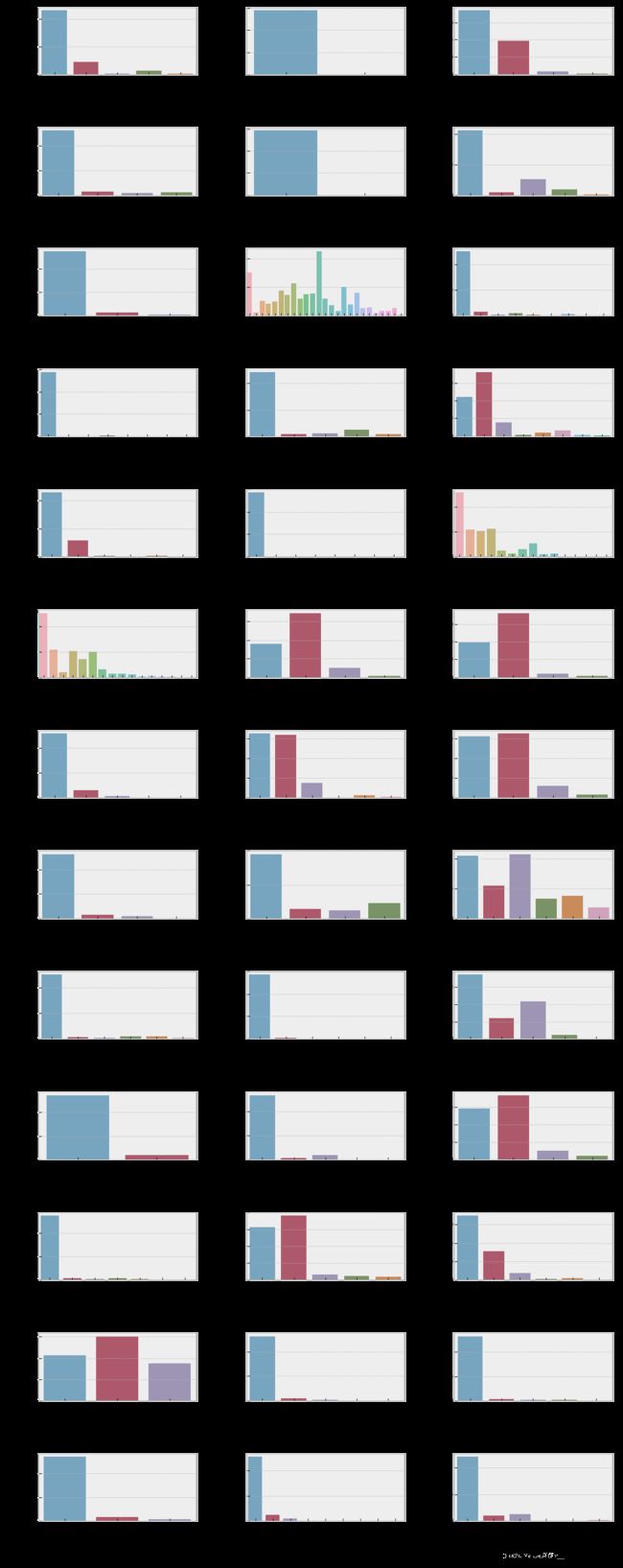
fig, axes = plt.subplots(round(len(df_not_num.columns) / 3), 3, figsize=(12, 30))

for i, ax in enumerate(fig.axes):
    if i < len(df_not_num.columns):
        ax.set_xticklabels(ax.xaxis.get_majorticklabels(), rotation=45)
        sns.countplot(x=df_not_num.columns[i], alpha=0.7, data=df_not_num, ax=ax)  # bar plots showing the counts of observations in each categorical bin

fig.tight_layout()

 

你可以看到，对于一些属性（Utilities、Heating、GarageCond、Functional）来说，有一个值是主要的。这些特征不携带进一步建模的信息。

用分类特征工作

替换值
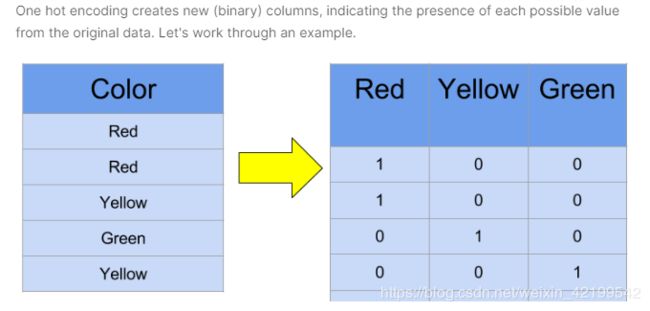
编码标签Encoding labels
一热编码One-Hot encoding
二进制编码Binary encoding
后向差异编码Backward difference encoding
杂项特征Miscellaneous features

# convert categorical variable into dummy
data_with_dummies = pd.get_dummies(data_without_nan.dropna())
data_with_dummies.head()

MSSubClass	LotFrontage	LotArea	OverallQual	OverallCond	YearBuilt	YearRemodAdd	MasVnrArea	BsmtFinSF1	BsmtFinSF2	...	SaleType_ConLD	SaleType_ConLI	SaleType_ConLw	SaleType_New	SaleType_WD	SaleCondition_Abnorml	SaleCondition_Alloca	SaleCondition_Family	SaleCondition_Normal	SaleCondition_Partial
1	20	80.0	9600	6	8	1976	1976	0.0	978	0	...	0	0	0	0	1	0	0	0	1	0
2	60	68.0	11250	7	5	2001	2002	162.0	486	0	...	0	0	0	0	1	0	0	0	1	0
3	70	60.0	9550	7	5	1915	1970	0.0	216	0	...	0	0	0	0	1	1	0	0	0	0
4	60	84.0	14260	8	5	2000	2000	350.0	655	0	...	0	0	0	0	1	0	0	0	1	0
6	20	75.0	10084	8	5	2004	2005	186.0	1369	0	...	0	0	0	0	1	0	0	0	1	0

5 row

MSSubClass	MSZoning	LotFrontage	LotArea	Street	LotShape	LandContour	Utilities	LotConfig	LandSlope	...	EnclosedPorch	3SsnPorch	ScreenPorch	PoolArea	MiscVal	MoSold	YrSold	SaleType	SaleCondition	SalePrice
0	60	RL	65.0	8450	Pave	Reg	Lvl	AllPub	Inside	Gtl	...	0	0	0	0	0	2	2008	WD	Normal	208500
1	20	RL	80.0	9600	Pave	Reg	Lvl	AllPub	FR2	Gtl	...	0	0	0	0	0	5	2007	WD	Normal	181500
2	60	RL	68.0	11250	Pave	IR1	Lvl	AllPub	Inside	Gtl	...	0	0	0	0	0	9	2008	WD	Normal	223500
3	70	RL	60.0	9550	Pave	IR1	Lvl	AllPub	Corner	Gtl	...	272	0	0	0	0	2	2006	WD	Abnorml	140000
4	60	RL	84.0	14260	Pave	IR1	Lvl	AllPub	FR2	Gtl	...	0	0	0	0	0	12	2008	WD	Normal	250000

5 rows × 76 columns

data_without_nan.head()

MSSubClass	MSZoning	LotFrontage	LotArea	Street	LotShape	LandContour	Utilities	LotConfig	LandSlope	...	EnclosedPorch	3SsnPorch	ScreenPorch	PoolArea	MiscVal	MoSold	YrSold	SaleType	SaleCondition	SalePrice
0	60	RL	65.0	8450	Pave	Reg	Lvl	AllPub	Inside	Gtl	...	0	0	0	0	0	2	2008	WD	Normal	208500
1	20	RL	80.0	9600	Pave	Reg	Lvl	AllPub	FR2	Gtl	...	0	0	0	0	0	5	2007	WD	Normal	181500
2	60	RL	68.0	11250	Pave	IR1	Lvl	AllPub	Inside	Gtl	...	0	0	0	0	0	9	2008	WD	Normal	223500
3	70	RL	60.0	9550	Pave	IR1	Lvl	AllPub	Corner	Gtl	...	272	0	0	0	0	2	2006	WD	Abnorml	140000
4	60	RL	84.0	14260	Pave	IR1	Lvl	AllPub	FR2	Gtl	...	0	0	0	0	0	12	2008	WD	Normal	250000

5 rows × 76 columns

变量选择
因此，在NaN的清洗阶段，所有迹象都被过滤掉了，除了： 巷子里的游泳池QC围栏MiscFeature.

经过定量特征的图形分析，看到了最适合进一步建立模型。1stFlrSF GarageArea GrLivArea LotFrontage TotalBsmtSF

通过与被调查变量SalePrice的相关性：OverallQual GrLivArea 2ndFlrSF。

根据各变量之间的相关性，有必要取其一FlrSF或TotalBsmtSF进行分析（相关系数0.82）。

按回归图：TotalBsmtSF GrLivArea 1stFlrSF GarageArea

其中优质功能：邻里外景1st / Exterior2nd HouseStyle BsmtFinType1。

最后一组：1stFlrSF(或TotalBsmtSF)、GarageArea、GrLivArea、LotFrontage、OverallQual(意义更大)、2ndFlrSF(可能要分类修改)、Neighborhood、Exterior1st(或Exterior2nd)、HouseStyle和BsmtFinType1。