CTC loss的几种解码方法:贪心搜索 (greedy search)、束搜索(Beam Search)、前缀束搜索(Prefix Beam Search)
CTC loss的几种解码方法:贪心搜索 (greedy search)、束搜索(Beam Search)、前缀束搜索(Prefix Beam Search)
前言:
预测新的样本输入对应的输出字符串,这涉及到解码。按照最大似然准则,最优的解码结果为:
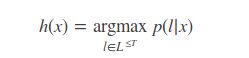
例:

如上图的例子,按照时间序列展开得到栅格网络,解码的过程相当于空间搜索, 求取穷举的所有可能字符串序列中概率最大的那个。我们可以选择暴力的解码策略:穷举搜索,但时间复杂度是指数级的N^{T},显然不可行。
然而,上式不存在已知的高效解法。下面介绍几种实用的近似破解码方法。
1 贪心搜索 (greedy search)
原理:
虽然 p(l|x) 难以有效的计算,但是由于 CTC 的独立性假设,对于某个具体的字符串 π(去 blank 前),确容易计算:
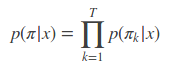
因此,我们放弃寻找使 p(l|x) 最大的字符串,退而寻找一个使 p(π|x) 最大的字符串,即:
![]()
其中,

简化后,解码过程(构造 π⋆)变得非常简单(基于独立性假设): 在每个时刻输出概率最大的字符:
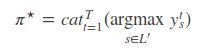
Greedy search 是在每一步选择概率最大的输出值,这样就可以得到最终解码的输出序列(如上图例子,最终解码的输出序列l=blank)。然而,CTC网络的输出序列只对应了搜索空间的一条路径,一个最终标签可对应搜索空间的N条路径,所以概率最大的路径并不等于最终标签的概率最大,即不是最优解(如上图例子,最优解是p(l=b)而不是p(l=blank))。
图示:

代码:
def remove_blank(labels, blank=0):
import numpy as np
# 求每一列(即每个时刻)中最大值对应的softmax值
def softmax(logits):
# 注意这里求e的次方时,次方数减去max_value其实不影响结果,因为最后可以化简成教科书上softmax的定义
# 次方数加入减max_value是因为e的x次方与x的极限(x趋于无穷)为无穷,很容易溢出,所以为了计算时不溢出,就加入减max_value项
# 次方数减去max_value后,e的该次方数总是在0到1范围内。
max_value = np.max(logits, axis=1, keepdims=True)
exp = np.exp(logits - max_value)
exp_sum = np.sum(exp, axis=1, keepdims=True)
dist = exp / exp_sum
return dist
def remove_blank(labels, blank=0):
new_labels = []
# 合并相同的标签
previous = None
for l in labels:
if l != previous:
new_labels.append(l)
previous = l
# 删除blank
new_labels = [l for l in new_labels if l != blank]
return new_labels
def insert_blank(labels, blank=0):
new_labels = [blank]
for l in labels:
new_labels += [l, blank]
return new_labels
def greedy_decode(y, blank=0):
# 按列取最大值,即每个时刻t上最大值对应的下标
raw_rs = np.argmax(y, axis=1)
# 移除blank,值为0的位置表示这个位置是blank
rs = remove_blank(raw_rs, blank)
return raw_rs, rs
np.random.seed(1111)
y_test = softmax(np.random.random([20, 6]))
label_have_blank, label_no_blank = greedy_decode(y_test)
print(label_have_blank)
print(label_no_blank)
2 束搜索(Beam Search)
贪心搜索的性能非常受限, 这种方法忽略了一个输出可能对应多个对齐结果。很多时候,如果我们能拿到nearbest的路径,后续可以利用其他信息来进一步优化搜索的结果。束搜索能近似找出 top 最优的若干条路径。
原理:
基本原理是通过 t i − 1 t_{i-1} ti−1中beamsize 个序列,每个序列分别连接 t i t_{i} ti中beamsize个节点,得到 beamsize个新序列及对应的score,然后按照score从大到小的顺序选出前beamSize个序列,依次推进。
图示:
假设 beamsize为2
t=1时:

这个时候只会将两个概率最大的节点放进路径集合中,即有两条路径。
t=2时:
上面的两个路径每个路径都会和下一个时间点的每一项组成新的路径,因此一共有 b e a m s i z e × V = 2 ∗ 3 = 6 beamsize\times V=2*3=6 beamsize×V=2∗3=6个新路径。
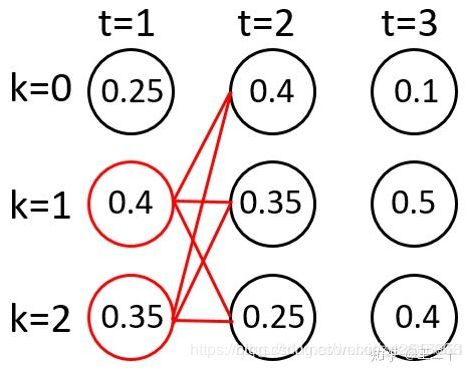
然后我们还是只保留概率最大的两条路径(次大的两个路径相等,这里舍弃掉一个)。
 t=3时:
t=3时:

和t=2时类似,又组成了新的6条路径。我们还是取概率最大的两条路径。
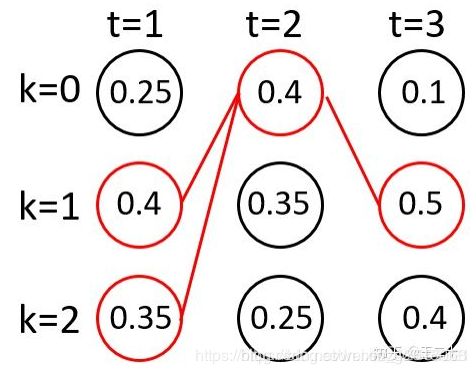
实际使用该算法时,往往取前20,这里前2只是为了方便举例。
更加直观的图,beamsize取3
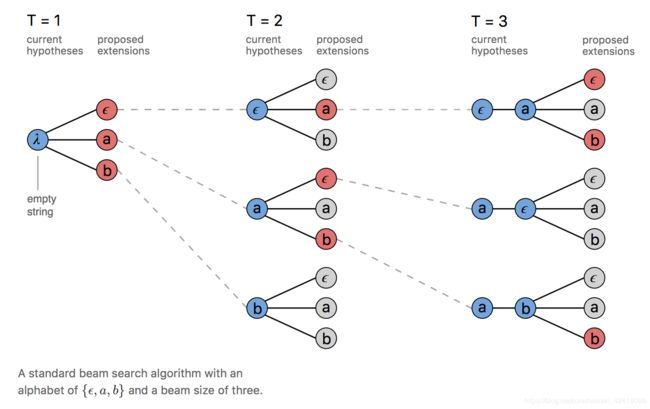
代码:
import numpy as np
# 求每一列(即每个时刻)中最大值对应的softmax值
def softmax(logits):
# 注意这里求e的次方时,次方数减去max_value其实不影响结果,因为最后可以化简成教科书上softmax的定义
# 次方数加入减max_value是因为e的x次方与x的极限(x趋于无穷)为无穷,很容易溢出,所以为了计算时不溢出,就加入减max_value项
# 次方数减去max_value后,e的该次方数总是在0到1范围内。
max_value = np.max(logits, axis=1, keepdims=True)
exp = np.exp(logits - max_value)
exp_sum = np.sum(exp, axis=1, keepdims=True)
dist = exp / exp_sum
return dist
def remove_blank(labels, blank=0):
new_labels = []
# 合并相同的标签
previous = None
for l in labels:
if l != previous:
new_labels.append(l)
previous = l
# 删除blank
new_labels = [l for l in new_labels if l != blank]
return new_labels
def insert_blank(labels, blank=0):
new_labels = [blank]
for l in labels:
new_labels += [l, blank]
return new_labels
def beam_decode(y, beam_size=10):
# y是个二维数组,记录了所有时刻的所有项的概率
T, V = y.shape
# 将所有的y中值改为log是为了防止溢出,因为最后得到的p是y1..yn连乘,且yi都在0到1之间,可能会导致下溢出
# 改成log(y)以后就变成连加了,这样就防止了下溢出
log_y = np.log(y)
# 初始的beam
beam = [([], 0)]
# 遍历所有时刻t
for t in range(T):
# 每个时刻先初始化一个new_beam
new_beam = []
# 遍历beam
for prefix, score in beam:
# 对于一个时刻中的每一项(一共V项)
for i in range(V):
# 记录添加的新项是这个时刻的第几项,对应的概率(log形式的)加上新的这项log形式的概率(本来是乘的,改成log就是加)
new_prefix = prefix + [i]
new_score = score + log_y[t, i]
# new_beam记录了对于beam中某一项,将这个项分别加上新的时刻中的每一项后的概率
new_beam.append((new_prefix, new_score))
# 给new_beam按score排序
new_beam.sort(key=lambda x: x[1], reverse=True)
# beam即为new_beam中概率最大的beam_size个路径
beam = new_beam[:beam_size]
return beam
np.random.seed(1111)
y_test = softmax(np.random.random([20, 6]))
beam_chosen = beam_decode(y_test, beam_size=100)
for beam_string, beam_score in beam_chosen[:20]:
print(remove_blank(beam_string), beam_score)
运行结果如下:
[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.261797539205567
[1, 3, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.279020152518033
[1, 3, 5, 1, 5, 3, 4, 2, 3, 4, 5, 3, 1, 3] -29.300726142201842
[1, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.310307014773972
[1, 3, 5, 1, 5, 3, 4, 2, 3, 3, 5, 3, 1, 3] -29.31794875551431
[1, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.327529628086438
[1, 3, 5, 1, 5, 4, 3, 4, 5, 3, 1, 3] -29.331572723457334
[1, 3, 5, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.33263180992451
[1, 3, 5, 4, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.334649090836038
[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.33969505198154
[1, 3, 5, 2, 1, 5, 3, 4, 3, 4, 5, 3, 1, 3] -29.339823066915415
[1, 3, 5, 1, 5, 4, 3, 3, 5, 3, 1, 3] -29.3487953367698
[1, 5, 1, 5, 3, 4, 2, 3, 4, 5, 3, 1, 3] -29.349235617770248
[1, 3, 5, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.349854423236977
[1, 3, 5, 1, 5, 3, 4, 3, 4, 5, 3, 3] -29.350803198551016
[1, 3, 5, 4, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.351871704148504
[1, 3, 5, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.356917665294006
[1, 3, 5, 2, 1, 5, 3, 4, 3, 3, 5, 3, 1, 3] -29.35704568022788
[1, 3, 5, 1, 5, 3, 4, 5, 4, 5, 3, 1, 3] -29.363802591012263
[1, 5, 1, 5, 3, 4, 2, 3, 3, 5, 3, 1, 3] -29.366458231082714
Process finished with exit code 0
可以看到log形式的score连加的结果都是负数,这是因为logx,当x属于0到1之间时logx为负的。
3 前缀束搜索(Prefix Beam Search)
参考论文:
First-Pass Large Vocabulary Continuous Speech Recognition using Bi-Directional Recurrent DNNs.
有许多不同的路径在many-to-one map的过程中是相同的,但beam search却会将一部分舍去,这导致了很多有用的信息被舍弃了。
比如 t = 2 t=2 t=2中, [ 0 , 2 ] [0,2] [0,2] 和 [ 2 , 0 ] [2,0] [2,0] 经过many-to-one map后相同,虽然两者的概率都不高,但两者加起来的概率很高,如果忽略这一点而直接舍弃掉他们是很不明智的一种做法。这种朴素的想法就催生了prefix beam search。基本的思想是将记录prefix的时候不在记录raw sequence,而是记录去掉blank和duplicate的sequence(具体步骤较复杂,会同时保留duplicate的和没duplicate得序列)。前缀束搜索(Prefix Beam Search)方法,可以在搜索过程中不断的合并相同的前缀。
具体较复杂,不过读者弄懂beam search后再想想prefix beam search的流程不是很难,主要弄懂probabilityWithBlank和probabilityNoBlank分别代表最后一个字符是空格和最后一个字符不是空格的概率即可。
import numpy as np
from collections import defaultdict
ninf = float("-inf")
# 求每一列(即每个时刻)中最大值对应的softmax值
def softmax(logits):
# 注意这里求e的次方时,次方数减去max_value其实不影响结果,因为最后可以化简成教科书上softmax的定义
# 次方数加入减max_value是因为e的x次方与x的极限(x趋于无穷)为无穷,很容易溢出,所以为了计算时不溢出,就加入减max_value项
# 次方数减去max_value后,e的该次方数总是在0到1范围内。
max_value = np.max(logits, axis=1, keepdims=True)
exp = np.exp(logits - max_value)
exp_sum = np.sum(exp, axis=1, keepdims=True)
dist = exp / exp_sum
return dist
def remove_blank(labels, blank=0):
new_labels = []
# 合并相同的标签
previous = None
for l in labels:
if l != previous:
new_labels.append(l)
previous = l
# 删除blank
new_labels = [l for l in new_labels if l != blank]
return new_labels
def insert_blank(labels, blank=0):
new_labels = [blank]
for l in labels:
new_labels += [l, blank]
return new_labels
def _logsumexp(a, b):
'''
np.log(np.exp(a) + np.exp(b))
'''
if a < b:
a, b = b, a
if b == ninf:
return a
else:
return a + np.log(1 + np.exp(b - a))
def logsumexp(*args):
'''
from scipy.special import logsumexp
logsumexp(args)
'''
res = args[0]
for e in args[1:]:
res = _logsumexp(res, e)
return res
def prefix_beam_decode(y, beam_size=10, blank=0):
T, V = y.shape
log_y = np.log(y)
# 最后一个字符是blank与最后一个字符为non-blank两种情况
beam = [(tuple(), (0, ninf))]
# 对于每一个时刻t
for t in range(T):
# 当我使用普通的字典时,用法一般是dict={},添加元素的只需要dict[element] =value即可,调用的时候也是如此
# dict[element] = xxx,但前提是element字典里,如果不在字典里就会报错
# defaultdict的作用是在于,当字典里的key不存在但被查找时,返回的不是keyError而是一个默认值
# dict =defaultdict( factory_function)
# 这个factory_function可以是list、set、str等等,作用是当key不存在时,返回的是工厂函数的默认值
# 这里就是(ninf, ninf)是默认值
new_beam = defaultdict(lambda: (ninf, ninf))
# 对于beam中的每一项
for prefix, (p_b, p_nb) in beam:
for i in range(V):
# beam的每一项都加上时刻t中的每一项
p = log_y[t, i]
# 如果i中的这项是blank
if i == blank:
# 将这项直接加入路径中
new_p_b, new_p_nb = new_beam[prefix]
new_p_b = logsumexp(new_p_b, p_b + p, p_nb + p)
new_beam[prefix] = (new_p_b, new_p_nb)
continue
# 如果i中的这一项不是blank
else:
end_t = prefix[-1] if prefix else None
# 判断之前beam项中的最后一个元素和i的元素是不是一样
new_prefix = prefix + (i,)
new_p_b, new_p_nb = new_beam[new_prefix]
# 如果不一样,则将i这项加入路径中
if i != end_t:
new_p_nb = logsumexp(new_p_nb, p_b + p, p_nb + p)
else:
new_p_nb = logsumexp(new_p_nb, p_b + p)
new_beam[new_prefix] = (new_p_b, new_p_nb)
# 如果一样,保留现有的路径,但是概率上要加上新的这个i项的概率
if i == end_t:
new_p_b, new_p_nb = new_beam[prefix]
new_p_nb = logsumexp(new_p_nb, p_nb + p)
new_beam[prefix] = (new_p_b, new_p_nb)
# 给新的beam排序并取前beam_size个
beam = sorted(new_beam.items(), key=lambda x: logsumexp(*x[1]), reverse=True)
beam = beam[:beam_size]
return beam
np.random.seed(1111)
y_test = softmax(np.random.random([20, 6]))
beam_test = prefix_beam_decode(y_test, beam_size=100)
for beam_string, beam_score in beam_test[:20]:
print(remove_blank(beam_string), beam_score)
将理解部分中的五种情况分别标记为1-5, 程序中if i == blank对应第1和3种情况,合并前缀中末尾字符为blank和不是blank的路径。if i != end_t对应第 4种情况 else if i = end_t对应第5种情况。
关于当前字符和前缀最后一个字符相等的两种情况, 一种是prefix 经过many-to-one map之前,最后一个label是blank, 另一种不是blank. 如prefix 为1, 未经过many-to-one map之前分别为[1, 0]和[0,1] 如果t=3,那么新的序列第一种情况应该是[1,1],第二种情况是[1],这就对应了一个加了新的label进来, 一个是keep current prefix. 对应图示中, 当输出的前缀字符串遇上重复字符时,可以映射到两个输出,当T=3时,前缀包含a,遇上新的a,则[a]和[a,a]两个输出都是有效的。
logSumExp()的作用:
https://zhuanlan.zhihu.com/p/39455488
参考
https://www.twblogs.net/a/5c0cb4a0bd9eee5e41830d90/zh-cn
https://www.jianshu.com/p/0cca89f64987
https://zhuanlan.zhihu.com/p/39266552

