LeetCode 第199场周赛 题解+代码
目录
- 一、5472. 重新排列字符串 Easy
- 方法:暴力
- 二、5473. 灯泡开关 IV Medium
- 方法:从左往右,只要和flag不一致,就翻转
- 三、5474. 好叶子节点对的数量 Medium
- 方法:dfs
- 四、5462. 压缩字符串 II Hard
- 方法:不会做,晚上补
一、5472. 重新排列字符串 Easy
通过的用户数3797
尝试过的用户数3843
用户总通过次数3856
用户总提交次数4641
题目难度Easy
给你一个字符串 s 和一个 长度相同 的整数数组 indices 。
请你重新排列字符串 s ,其中第 i 个字符需要移动到 indices[i] 指示的位置。
返回重新排列后的字符串。
示例 1:
输入:s = "codeleet", indices = [4,5,6,7,0,2,1,3]
输出:"leetcode"
解释:如图所示,"codeleet" 重新排列后变为 "leetcode" 。
示例 2:
输入:s = "abc", indices = [0,1,2]
输出:"abc"
解释:重新排列后,每个字符都还留在原来的位置上。
示例 3:
输入:s = "aiohn", indices = [3,1,4,2,0]
输出:"nihao"
示例 4:
输入:s = "aaiougrt", indices = [4,0,2,6,7,3,1,5]
输出:"arigatou"
示例 5:
输入:s = "art", indices = [1,0,2]
输出:"rat"
提示:
- s.length == indices.length == n
- 1 <= n <= 100
- s 仅包含小写英文字母。
- 0 <= indices[i] < n
- indices 的所有的值都是唯一的(也就是说,indices 是整数 0 到 n - 1 形成的一组排列)。
方法:暴力
代码一
class Solution {
public String restoreString(String s, int[] indices) {
char[] chars = s.toCharArray();
char[] resultArray = new char[s.length()];
int j = 0;
for (int i : indices) {
resultArray[i] = chars[j++];
}
return new String(resultArray);
}
}
代码二
class Solution {
public String restoreString(String s, int[] indices) {
char[] ans = new char[s.length()];
for(int i = 0; i < s.length(); i++){
ans[indices[i]] = s.charAt(i);
}
return new String(ans);
}
}
二、5473. 灯泡开关 IV Medium
通过的用户数2796
尝试过的用户数2995
用户总通过次数2811
用户总提交次数4128
题目难度Medium
房间中有 n 个灯泡,编号从 0 到 n-1 ,自左向右排成一行。最开始的时候,所有的灯泡都是 关 着的。
请你设法使得灯泡的开关状态和 target 描述的状态一致,其中 target[i] 等于 1 第 i 个灯泡是开着的,等于 0 意味着第 i 个灯是关着的。
有一个开关可以用于翻转灯泡的状态,翻转操作定义如下:
选择当前配置下的任意一个灯泡(下标为 i )
翻转下标从 i 到 n-1 的每个灯泡
翻转时,如果灯泡的状态为 0 就变为 1,为 1 就变为 0 。
返回达成 target 描述的状态所需的 最少 翻转次数。
示例 1:
输入:target = "10111"
输出:3
解释:初始配置 "00000".
从第 3 个灯泡(下标为 2)开始翻转 "00000" -> "00111"
从第 1 个灯泡(下标为 0)开始翻转 "00111" -> "11000"
从第 2 个灯泡(下标为 1)开始翻转 "11000" -> "10111"
至少需要翻转 3 次才能达成 target 描述的状态
示例 2:
输入:target = "101"
输出:3
解释:"000" -> "111" -> "100" -> "101".
示例 3:
输入:target = "00000"
输出:0
示例 4:
输入:target = "001011101"
输出:5
提示:
1 <= target.length <= 10^5
target[i] == ‘0’ 或者 target[i] == ‘1’
方法:从左往右,只要和flag不一致,就翻转
class Solution {
public int minFlips(String target) {
char flag = '0';
int count = 0;
for (int i = 0; i < target.length(); i++) {
if (target.charAt(i) != flag) {
count++;
if (target.charAt(i) == '1') {
flag = '1';
} else {
flag = '0';
}
//flag = target.charAt(i) == '1' ? '1' : '0';
}
}
return count;
}
}
三、5474. 好叶子节点对的数量 Medium
通过的用户数838
尝试过的用户数1120
用户总通过次数846
用户总提交次数1664
题目难度Medium
给你二叉树的根节点 root 和一个整数 distance 。
如果二叉树中两个 叶 节点之间的 最短路径长度 小于或者等于 distance ,那它们就可以构成一组 好叶子节点对 。
返回树中 好叶子节点对的数量 。
输入:root = [1,2,3,null,4], distance = 3
输出:1
解释:树的叶节点是 3 和 4 ,它们之间的最短路径的长度是 3 。这是唯一的好叶子节点对。
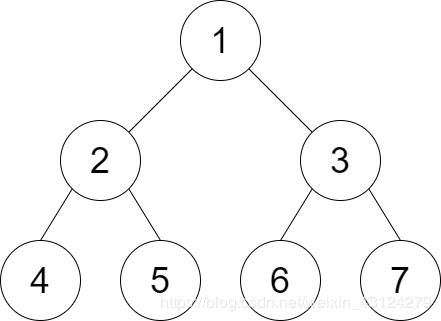
输入:root = [1,2,3,4,5,6,7], distance = 3
输出:2
解释:好叶子节点对为 [4,5] 和 [6,7] ,最短路径长度都是 2 。但是叶子节点对 [4,6] 不满足要求,因为它们之间的最短路径长度为 4 。
示例 3:
输入:root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
输出:1
解释:唯一的好叶子节点对是 [2,5] 。
示例 4:
输入:root = [100], distance = 1
输出:0
示例 5:
输入:root = [1,1,1], distance = 2
输出:1
提示:
- tree 的节点数在 [1, 2^10] 范围内。
- 每个节点的值都在 [1, 100] 之间。
- 1 <= distance <= 10
方法:dfs
代码一
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int countPairs(TreeNode root, int distance) {
dfs(root, distance);
return ans;
}
int ans = 0;
public void handle(TreeNode root, int[] state, int d){
int[] ret = dfs(root, d);
for(int i = 0; i <= d; i++){
for(int j = 0; j <= d; j++){
if(i + j + 1 <= d){
ans += ret[i] * state[j];
}
}
}
for(int i = 0; i < d; i++){
state[i + 1] += ret[i];
}
}
public int[] dfs(TreeNode root, int d){
int[] state = new int[d + 1];
if(root.left == null && root.right == null){
state[0] = 1;
return state;
}
if(root.left != null){
handle(root.left, state, d);
}
if(root.right != null){
handle(root.right, state, d);
}
return state;
}
}
代码二
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int ans = 0;
public int countPairs(TreeNode root, int distance) {
dfs(root, distance);
return ans;
}
private List<Integer> dfs(TreeNode root, int distance){
if(root.left == null && root.right == null){
List<Integer> list = new ArrayList<>();
list.add(0);
return list;
}
List<Integer> left = new ArrayList<>();
if(root.left != null){
left = dfs(root.left, distance);
}
List<Integer> right = new ArrayList<>();
if(root.right != null){
right = dfs(root.right, distance);
}
if(left.size() > 0 && right.size() > 0){
for(int t:left){
for(int t1:right){
if(t + t1 + 2 <= distance){
ans++;
}
}
}
}
List<Integer> list = new ArrayList<>();
for(int t:left){
list.add(t+1);
}
for(int t:right){
list.add(t+1);
}
return list;
}
}
四、5462. 压缩字符串 II Hard
通过的用户数30
尝试过的用户数178
用户总通过次数31
用户总提交次数400
题目难度Hard
行程长度编码 是一种常用的字符串压缩方法,它将连续的相同字符(重复 2 次或更多次)替换为字符和表示字符计数的数字(行程长度)。例如,用此方法压缩字符串 “aabccc” ,将 “aa” 替换为 “a2” ,“ccc” 替换为` “c3” 。因此压缩后的字符串变为 “a2bc3” 。
注意,本问题中,压缩时没有在单个字符后附加计数 ‘1’ 。
给你一个字符串 s 和一个整数 k 。你需要从字符串 s 中删除最多 k 个字符,以使 s 的行程长度编码长度最小。
请你返回删除最多 k 个字符后,s 行程长度编码的最小长度 。
示例 1:
输入:s = "aaabcccd", k = 2
输出:4
解释:在不删除任何内容的情况下,压缩后的字符串是 "a3bc3d" ,长度为 6 。最优的方案是删除 'b' 和 'd',这样一来,压缩后的字符串为 "a3c3" ,长度是 4 。
示例 2:
输入:s = "aabbaa", k = 2
输出:2
解释:如果删去两个 'b' 字符,那么压缩后的字符串是长度为 2 的 "a4" 。
示例 3:
输入:s = "aaaaaaaaaaa", k = 0
输出:3
解释:由于 k 等于 0 ,不能删去任何字符。压缩后的字符串是 "a11" ,长度为 3 。
提示:
- 1 <= s.length <= 100
- 0 <= k <= s.length
- s 仅包含小写英文字母