Naive Bayes

写在开头
　　最近在学习一些关于机器学习的基础算法，结合学习Peter Harrington的《机器学习实战》和李航老师的《统计学习方法》两本书以及网上前辈的笔记，写下了以下的学习过程。
　　代码环境：Pytharm/Python3.7
　　内容有参考也有自己的想法，由于自己的理解不足，文章肯定存在很多错误，还恳请各位批评指正。

一. 关于Naive Bayes
　　贝叶斯分类器是一类分类算法的总称，是两种最为广泛的分类模型之一，另一种就是上篇中的决策树了。贝叶斯分类均以贝叶斯定理为基础，朴素贝叶斯是贝叶斯分类中最简单的一种，是基于贝叶斯定理与特征条件独立假设的分类方法。
　　优点： 在数据较少的情况下仍然有效，可以处理多类别问题。
　　缺点： 对于输入数据的准备方式较为敏感。
　　之前所学习的基于分类的K-means和决策树都是给出了分类的明确答案，但是分类势必是会产生错误结果，结合概率论的相关知识，我们在分类时，可以给出类别估计值，进而将赋予数据最优类别猜测。就分类而言，有时使用概率要比那些硬规则有效的多，贝叶斯准则和贝叶斯定理就是利用已知值来估计未知概率的方法。
　　据此，我们可以使用概率论进行分类，首先从一个最简单的概率分类器开始，进而给出一些假设来学习朴素贝叶斯分类器。之所以称之为“朴素”，是因为在整个过程当中我们都使用的是最原始，最简单的假设。贝叶斯算法的基础是概率问题，分类的原理是通过某对象的先验概率，利用贝叶斯公式计算出它的后验概率（对象属于某一类的概率），选取具有最大后验概率的类作为该对象所属的类。就像那个特别有名的例子：在大街上碰到一个黑人，要让你猜测他是哪个洲的，你肯定首先会说非洲，为什么呢，因为黑人中非洲最多，在这里我们就选取了出现概率最大的类别。
　　分类算法这么多，要说贝叶斯分类器跟其它分类算法的区别，首先要说贝叶斯的分类准确率相对较高，而对于了解学习过程，还是决策树更适合。
二. 贝叶斯定理
　　贝叶斯定理对大家而言，应该都不会太陌生，今天再温习一下。首先说一下与贝叶斯定理密不可分的条件概率：P(A|B) = P(AB) / P(B),其中P(A|B)表示的B发生的情况下A发生的概率，这就是条件概率。
　　为什么要提出贝叶斯定理呢？因为现实生活中的很多问题，都是很容易求出P(A|B)，但P(B|A)却很难求出，而P(B|A)却相对更有用，由此贝叶斯定理产生。
定义为：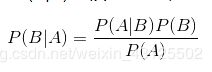
三. 朴素贝叶斯分类器
　　分类的原理是通过某对象的先验概率，利用贝叶斯公式计算出它的后验概率（对象属于某一类的概率），选取具有最大后验概率的类作为该对象所属的类。把Ａ和Ｂ看作是随机变量，那么P(B|A)就是Ｂ的后验概率，P(B)是B的先验概率。
对于朴素贝叶斯分类器，要做出两个假设：
　　（1）特征之间相互独立，即一个特征的出现于其它相邻的特征并无关系；
　　（2）每个特征同等重要。
　　相信大家已经了解了什么是条件概率和贝叶斯公式了，那么对于一个两类问题，我们将贝叶斯公式修改成以下形式：

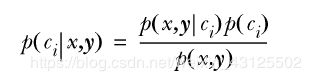
可以定义分类准则为：
　　如果Ｐ（Ｃ１｜ｘ，ｙ）>Ｐ（Ｃ２｜ｘ，ｙ），那么属于类别C1
　　如果Ｐ（Ｃ１｜ｘ，ｙ）<Ｐ（Ｃ２｜ｘ，ｙ），那么属于类别C2
　　使用贝叶斯准则，可以通过已知的三个概率值来计算未知的概率值。实际上可以只用求取分子大小，就能获得分类结果。
　　下面给出整个贝叶斯分类器实现的源代码，定义的每一个函数都有详细的介绍，对于一些关键代码也给出了较为详细的个人看法仅供参考。

贝叶斯分类器源码

import numpy


# -------------------创建实验样本------------------


def loadDataSet():
    # 用于训练算法的数据，classVec用于注明包含哪些词就属于侮辱语言
    trainSet = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]  # 向量区分词汇类别，1 是侮辱语言, 0 no
    return trainSet, classVec


# --------创建一个包含在文档矩阵中出现的不重复词的列表(去除重复单词)-----------
# 创建了一个不含有重复单词的列表，用于处理用于训练算法的数据文档
def createVocabList(dataSet):
    vocabSet = set([])  # 创建一个空集
    for document in dataSet:
        #或运算保证了不会出现重复单词
        vocabSet = vocabSet | set(document)
    return list(vocabSet)


# 词集模式
# ---------判断某个文档是否含有禁止的词汇-----------------
# 输入参数为词汇列表VacaList,注意是list和待检测的文档inputSet
def setOfWords2Vec(VacaList, inputSet):
    returnZeroOneVec = [0] * len(VacaList)  # 创建一个与词汇列表相同长度的向量，因为对应01输出
    for word in inputSet:
        if word in VacaList:
            # index（）函数可以索引子字符串在字符串中的位置，没找到就error，
            returnZeroOneVec[VacaList.index(word)] = 1
        else:
            print("the word '{}' not in the vocablist".format(word))
    # 最后返回的是检测之后词汇表对应的0/1值，1代表在待检测文档中出现了
    return returnZeroOneVec



# 词袋模式
# def bagOfWords2Vec(VacaList, inputSet):
#     returnZeroOneVec = [0] * len(VacaList)  # 创建一个与词汇列表相同长度的向量，因为对应01输出
#     for word in inputSet:
#         if word in VacaList:
#             # index（）函数可以索引子字符串在字符串中的位置，没找到就error
#             # 词袋模式下并不是只确定词出现了（出现就赋值1），而是进一步判断出现了几次
#             returnZeroOneVec[VacaList.index(word)] += 1
#         else:
#             print("the word '{}' not in the vocablist".format(word))
#     # 最后返回的是检测之后词汇表对应的0/1值，1代表在待检测文档中出现了
#     return returnZeroOneVec


# -----------分类器训练函数-----------------
# 输入参数trainMatrix为输入文档矩阵，trainCategory为输入数据的标签也是0/1
# 可以根据最后的概率数据，判断出哪些词是属于侮辱词汇）
def trainNB0(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)  # 矩阵行数
    numWords = len(trainMatrix[0])  # 矩阵列数
    pAbusive = sum(trainCategory) / float(numTrainDocs)  # 计算该文档属于侮辱性文档的概率（即P(c1)）
    # ones()是创造元素全为1的数组，不是列表
    # 初始化所有词语出现次数为1，分母初始化为0，避免概率值为0的情况
    p0Num = numpy.ones(numWords)
    p1Num = numpy.ones(numWords)  # change to ones()
    p0Denom = 2.0
    p1Denom = 2.0  # change to 2.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    # 由于在求P（wi|c1）时由很多小数相乘得来，会因数据过小而造成下溢出或者浮点数舍入导致错误
    p1Vect = numpy.log(p1Num / p1Denom)  # change to log()
    p0Vect = numpy.log(p0Num / p0Denom)  # change to log()
    return p0Vect, p1Vect, pAbusive


# ------------贝叶斯分类函数--------
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    # 求分子，由于之前log处理了，因此乘法变加法
    p1 = sum(vec2Classify * p1Vec) + numpy.log(pClass1)
    p0 = sum(vec2Classify * p0Vec) + numpy.log(1.0 - pClass1)
    #分母一样大不做比较，分子决定分类
    if p1 > p0:
        return 'badword'
    else:
        return 'goodword'


def main():
    trainSet, classVec = loadDataSet()
    vocabList = createVocabList(trainSet)
    # print(vocabList)
    # 把测试数据按照是否含有侮辱性词汇转换成0/1
    trainMat = []
    for postinDoc in trainSet:
        # append()这个函数和或运算完全不一样，这个函数是直接在列表后加列表，而不是加元素
        #因此trainMat产生的是一个与行数与trainSet一样，列数与vocabList一样的0/1矩阵。
        trainMat.append(setOfWords2Vec(vocabList, postinDoc))
    print(trainMat)
    p0Vect, p1Vect, pAbusive = trainNB0(numpy.array(trainMat), numpy.array(classVec))
    # 每次运行的结果都是不一样的，因为vocabList是随机排序的
    print(p0Vect, p1Vect, pAbusive, sep='\n')
    testEntry = ['love', 'my', 'dalmation']
    # 检测testEntry中是否含有vocabList中的词汇
    thisDoc = numpy.array(setOfWords2Vec(vocabList, testEntry))
    # 打印结果
    print('{} classified as:{} '.format(testEntry, classifyNB(thisDoc, p0Vect, p1Vect, pAbusive)))
    testEntry = ['stupid', 'garbage']
    thisDoc = numpy.array(setOfWords2Vec(vocabList, testEntry))
    print('{} classified as:{} '.format(testEntry, classifyNB(thisDoc, p0Vect, p1Vect, pAbusive)))


main()

四. 贝叶斯的应用_过滤垃圾邮件
　　垃圾邮件过滤源码

import numpy

# 读取文件内容
def list_all_files(rootdir):
    import os
    import numpy
    docList = []
    fullText = []
    classList = []
    fileName = []
    list = os.listdir(rootdir)  # 列出文件夹下所有的目录与文件
    for i in range(0, len(list)):
        path = os.path.join(rootdir, list[i])
        if os.path.isdir(path):
            fileName.extend(list_all_files(path))
        if os.path.isfile(path):
            fileName.append(path)
    for file in fileName:
        txt = open(file, encoding='gb18030', errors='ignore').read()  # 打开文件
        txt = txt.lower()  # 全部转化为小写字母
        for i in '!#$%^&*()_-+=/`~{}[]:;\'?<>,.':  # 去掉全部标点符号用空格代替
            txt = txt.replace(i, " ")
        wordsList = txt.split()  # split 默认用空格将字符串分隔并以列表形式返回
        docList.append(wordsList)
        fullText.extend(wordsList)
        classList = numpy.random.randint(0, 2, len(list))  # 输出只含0,1元素的一维数组,长度为len(list)
    return docList, fullText, classList


# 词集模式
# ---------判断某个文档是否含有禁止的词汇-----------------
# 输入参数为词汇列表VacaList,注意是list和待检测的文档inputSet
def setOfWords2Vec(VacaList, inputSet):
    returnZeroOneVec = [0] * len(VacaList)  # 创建一个与词汇列表相同长度的向量，因为对应01输出
    for word in inputSet:
        if word in VacaList:
            # index（）函数可以索引子字符串在字符串中的位置，没找到就error，
            returnZeroOneVec[VacaList.index(word)] = 1
        # else:
        #     print("the word '{}' not in the vocablist".format(word))
    # 最后返回的是检测之后词汇表对应的0/1值，1代表在待检测文档中出现了
    return returnZeroOneVec


# --------创建一个包含在文档矩阵中出现的不重复词的列表(去除重复单词)-----------
# 创建了一个不含有重复单词的列表，用于处理用于训练算法的数据文档
def createVocabList(dataSet):
    vocabSet = set([])  # 创建一个空集
    for document in dataSet:
        # 或运算保证了不会出现重复单词
        vocabList = vocabSet | set(document)
    return list(vocabList)


# -----------分类器训练函数-----------------
# 输入参数trainMatrix为输入文档矩阵，trainCategory为输入数据的标签也是0/1
# 可以根据最后的概率数据，判断出哪些词是属于侮辱词汇）
def trainNB0(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)  # 矩阵行数
    numWords = len(trainMatrix[0])  # 矩阵列数
    pAbusive = sum(trainCategory) / float(numTrainDocs)  # 计算该文档属于侮辱性文档的概率（即P(c1)）
    # ones()是创造元素全为1的数组，不是列表
    # 初始化所有词语出现次数为1，分母初始化为0，避免概率值为0的情况
    p0Num = numpy.ones(numWords)
    p1Num = numpy.ones(numWords)  # change to ones()
    p0Denom = 2.0
    p1Denom = 2.0  # change to 2.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    # 由于在求P（wi|c1）时由很多小数相乘得来，会因数据过小而造成下溢出或者浮点数舍入导致错误
    p1Vect = numpy.log(p1Num / p1Denom)  # change to log()
    p0Vect = numpy.log(p0Num / p0Denom)  # change to log()
    return p0Vect, p1Vect, pAbusive
# ------------贝叶斯分类函数--------
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    # 求分子，由于之前log处理了，因此乘法变加法
    p1 = sum(vec2Classify * p1Vec) + numpy.log(pClass1)
    p0 = sum(vec2Classify * p0Vec) + numpy.log(1.0 - pClass1)
    #分母一样大不做比较，分子决定分类
    if p1 > p0:
        return 1
    else:
        return 0

def main():
    import random
    import numpy
    # 读取文件
    docList, fullText, classList = list_all_files('ham')
    trainSet = []
    testSet = []
    trainClasses = []
    testClasses= []
    testSet = docList
    randomList = random.sample(range(0, 24), 10)  # 表示从[A,B]间随机生成N个数，结果以列表返回
    for i in randomList:
        trainSet.append(docList[i])
        trainClasses.append(classList[i])
    for i in range(25):
        if i not in randomList:
            testSet.append(docList[i])
            testClasses.append(classList[i])
    print(trainSet, testSet, sep='\n')
    # 开始使用产生的训练集训练分类器
    teainMat = []
    vocabList = createVocabList(docList)# 获取不重复词表
    for file in trainSet:
        teainMat.append(setOfWords2Vec(vocabList, file))
    p0Vect, p1Vect, pAbusive = trainNB0(teainMat, trainClasses)
    errorCount = 0
    for i in range(len(testClasses)):
        wordVector = numpy.array(setOfWords2Vec(vocabList, testSet[i]))
        if classifyNB(wordVector, p0Vect, p1Vect, pAbusive) != testClasses[i]:
            errorCount +=1
    print("错误率为：{}".format(errorCount/len(testSet)))

main()

整个程序首先进行文件处理，读取了一个文件夹下面所有的文件内容并进行格式处理，构成一个列表。
　　然后开始训练分类器，在读取的25封邮件中随机选择10封（可以更改这个数字，那么分类结果也会随之改变）作为训练集，剩下的作为测试集
　　最后就调用之前的贝叶斯分类算法进行邮件分类，并将分类结果与真实结果进行比较，输出错分类错误率判断分类器好坏。

参考文档：
［1］《机器学习实战》第四章
［2］https://www.cnblogs.com/ybjourney/p/4779488.html