【计算机组成原理】补码加减法和溢出检测
文章目录
- 补码加法
- 补码减法
- 溢出概念及其检测方法
补码加法
补码加法运算基本公式
定点整数: [ x + y ] 补 = [ x ] 补 + [ y ] 补 ( 结 果 m o d 2 n + 1 ) [x+y]_补 = [x]_补+[y]_补 \quad (结果\ mod\ 2^{n+1}) [x+y]补=[x]补+[y]补(结果 mod 2n+1)
定点小数: [ x + y ] 补 = [ x ] 补 + [ y ] 补 ( 结 果 m o d 2 ) [x+y]_补 = [x]_补+[y]_补 \quad (结果\ mod\ 2) [x+y]补=[x]补+[y]补(结果 mod 2)
例1: x = + 1001 , y = + 0101 , 求 x + y x= +1001, y=+0101, 求x+y x=+1001,y=+0101,求x+y
∵ [ x ] 补 = 0 1001 , [ y ] 补 = 0 0101 \because \ [x]_补 = 0\ 1001,\quad [y]_补=0\ 0101 ∵ [x]补=0 1001,[y]补=0 0101

∴ x + y = + 1110 \therefore x+y = +1110 ∴x+y=+1110
例2: x = + 1011 , y = − 0101 , 求 x + y x=+1011, y=-0101, 求x+y x=+1011,y=−0101,求x+y
∵ [ x ] 补 = 0 1011 , [ y ] 补 = 1 1011 \because [x]_补=0\ 1011, [y]_补 = 1\ 1011 ∵[x]补=0 1011,[y]补=1 1011
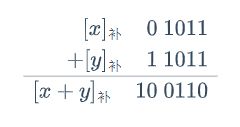
结果对 2 n + 1 2^{n+1} 2n+1取模
∴ x + y = + 0110 \therefore x+y = +0110 ∴x+y=+0110
计算机中加法是同过补码进行的, 这是为了在同一个运算器上另一种运算——减法. 两个数的补码相加等于两个分别求补码再相加, 最终结果对 2 n + 1 2^{n+1} 2n+1取模.
补码减法
补码减法基本运算公式
定点整数: [ x − y ] 补 = [ x ] 补 − [ y ] 补 = [ x ] 补 + [ − y ] 补 [x-y]_补 = [x]_补-[y]_补=[x]_补+[-y]_补 [x−y]补=[x]补−[y]补=[x]补+[−y]补
定点小数同上.
运算过程的重点是把 − [ y ] 补 ⇒ [ − y ] 补 -[y]_补 \Rightarrow [-y]_补 −[y]补⇒[−y]补
转换规则: 符号位和数值位均取反, 最后加1.
为什么符号位取反? 因为这个过程是把一个负数转换成一个正数, 所以符号位需要变.
为什么数值位取反? 取反后加1这个过程是对补码又求了一次补码, 最终数值位变成了原码, 又因为符号位取反, 所以这个数从负数变成了正数, 因此在这里又可以得出: 多次求补码, 可以使 原 码 ⇌ 互 转 补 码 原码 \overset{互转}{\rightleftharpoons} 补码 原码⇌互转补码.
例: 一个负数 [ − 001 ] ⇒ [ 1001 ] 原 ⇒ [ 1111 ] 补 ⟹ 再 求 补 码 [ 10001 ] 补 [-001] \Rightarrow [1001]_原 \Rightarrow [1111]_补 \overset{再求补码}{\Longrightarrow} [10001]_补 [−001]⇒[1001]原⇒[1111]补⟹再求补码[10001]补 , 此时的补码变成了原码.
溢出概念及其检测方法
当所存储的数超过二进制(固定长度)所能表示的值的范围时, 二进制所表示的数值出现错误, 这种现象称为溢出. 溢出并非都是坏处, 在将减法转换成加法(由补码完成)就利用了溢出的特性.
溢出分两种正溢出和负溢出, 当两个正数相加超出进制表示范围称为正溢出, 两个负数进行运算超出进制表示范围称为负溢出.
溢出只出现在良正数或负数相加.
溢出检测方法有两种: 变形补码判别法和单符号位法
变形补码采用双符号位表示补码, 任何正数的符号位都是"00", 任何负数的符号位都是"11", 运算后, 如果符号位变成"01"(正溢)或"10"(负溢)表示出现溢出.
| 符号位 | 结果 |
|---|---|
| 00 | 正数 |
| 01 | 溢出 |
| 10 | 溢出 |
| 11 | 负数 |
在电路中使用异或判断很方便.
单符号位法判断时采用1bit进位与符号位进行判断, 判断方式通上.
Q&A 请指正!