矩阵位移法计算三种桁架(静定,一次,二次超静定)
1
为 了 便 于 计 算 , 桁 架 弹 性 模 量 与 截 面 积 乘 积 E A = 1 , 所 有 杆 件 均 为 二 力 杆 \qquad为了便于计算,桁架弹性模量与截面积乘积EA=1,所有杆件均为二力杆 为了便于计算,桁架弹性模量与截面积乘积EA=1,所有杆件均为二力杆
只 讨 论 轴 向 变 形 。 三 结 构 均 在 左 上 节 点 受 一 水 平 向 右 , 和 竖 直 向 下 集 中 力 , 均 为 10 K N 只讨论轴向变形。三结构均在左上节点受一水平向右,和竖直向下集中力,均为10KN 只讨论轴向变形。三结构均在左上节点受一水平向右,和竖直向下集中力,均为10KN
import numpy as np
from math import sqrt,sin,cos,acos
np.set_printoptions(precision=2)
np.set_printoptions(suppress=True)
EA = 1
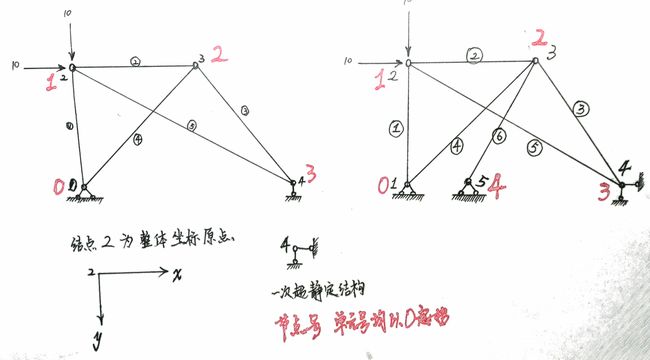
单 元 正 向 逆 时 针 旋 转 到 整 体 坐 标 系 X 轴 正 向 , 旋 转 角 不 得 大 于 π , 倒 数 第 二 个 必 须 是 [ 2 , 0 ] , 不 能 是 [ 0 , 2 ] 倒 数 第 一 个 必 须 是 [ 1 , 3 ] , 不 能 是 [ 3 , 1 ] 否 则 直 接 影 响 节 点 位 移 计 算 结 果 ! 单元正向逆时针旋转到整体坐标系X轴正向,旋转角不得大于\pi,\\ 倒数第二个必须是[2,0],不能是[0,2]\\ 倒数第一个必须是[1,3],不能是[3,1]\\ 否则直接影响节点位移计算结果! 单元正向逆时针旋转到整体坐标系X轴正向,旋转角不得大于π,倒数第二个必须是[2,0],不能是[0,2]倒数第一个必须是[1,3],不能是[3,1]否则直接影响节点位移计算结果!
nodeCoord = np.array([[0,-2],[0,0],[2,0],[3.5,-2]])
elemNode = np.array([[1,0],[1,2],[2,3],[2,0],[1,3]])
整 体 坐 标 系 下 单 元 刚 度 矩 阵 的 定 位 向 量 ( 单 刚 中 的 行 列 非 0 元 素 在 总 刚 中 的 位 置 ) 定 位 向 量 在 单 刚 组 装 成 总 刚 的 时 候 很 重 要 每 一 行 存 储 了 每 个 单 元 的 俩 端 节 点 约 束 信 息 分 别 为 u 1 , v 1 , u 2 , v 2 四 个 自 由 度 约 束 与 否 的 布 尔 值 定 位 向 量 非 0 元 素 为 结 构 中 尚 未 约 束 的 自 由 度 编 号 定 位 向 量 中 的 最 大 值 , 为 节 点 所 有 未 约 束 自 由 度 的 数 目 四 个 自 由 度 , 非 0 指 定 放 松 约 束 , 标 号 在 整 体 结 构 中 顺 次 递 增 整体坐标系下单元刚度矩阵的定位向量 (单刚中的行列非0元素 在总刚中的 位置)\\ 定位向量 在 单刚组装成总刚的时候很重要\\ 每一行存储了每个单元的俩端节点约束信息\\ 分别为u_1,v_1,u_2,v_2四个自由度约束与否的布尔值\\ 定位向量非0元素为 结构中尚未约束的自由度编号\\ 定位向量中的最大值,为节点所有未约束自由度的数目\\ 四个自由度,非0指定放松约束,标号在整体结构中顺次递增 整体坐标系下单元刚度矩阵的定位向量(单刚中的行列非0元素在总刚中的位置)定位向量在单刚组装成总刚的时候很重要每一行存储了每个单元的俩端节点约束信息分别为u1,v1,u2,v2四个自由度约束与否的布尔值定位向量非0元素为结构中尚未约束的自由度编号定位向量中的最大值,为节点所有未约束自由度的数目四个自由度,非0指定放松约束,标号在整体结构中顺次递增
lambda_k =np.array([[0,0,1,2],
[1,2,3,4],
[3,4,5,0],
[0,0,3,4],
[1,2,5,0]])
Forces = np.array([10,10,0,0,0])
上 面 的 定 位 矩 阵 第 四 行 [ 0 , 0 , 3 , 4 ] 改 成 了 [ 3 , 4 , 0 , 0 ] , 虽 然 位 移 计 算 结 果 依 然 正 确 但 是 [ 0 , 0 , 3 , 4 ] 对 应 的 杆 单 元 的 轴 力 变 成 了 正 解 相 反 数 上面的定位矩阵第四行[0,0,3,4]改成了[3,4,0,0],\\ 虽然位移计算结果依然正确\\ 但是[0,0,3,4]对应的杆单元 的轴力变成了正解相反数 上面的定位矩阵第四行[0,0,3,4]改成了[3,4,0,0],虽然位移计算结果依然正确但是[0,0,3,4]对应的杆单元的轴力变成了正解相反数
注 意 : 1 ) 单 元 正 向 逆 时 针 旋 转 到 整 体 坐 标 系 X 轴 正 向 , 旋 转 角 不 得 大 于 π , 这 必 须 满 足 2 ) 当 单 元 正 向 与 整 体 坐 标 系 X 轴 正 向 的 夹 角 小 于 90 ° 时 , 定 位 向 量 编 号 次 序 与 e l e m N o d e 单 元 节 点 次 序 一 致 , 3 ) 当 单 元 正 向 与 整 体 坐 标 系 X 轴 正 向 的 夹 角 大 于 90 ° 时 , 定 位 向 量 编 号 次 序 与 e l e m N o d e 单 元 节 点 次 序 相 反 , 所 以 l a m b d a _ k 第 四 行 单 元 节 点 次 序 为 [ 2 , 0 ] , 但 是 其 单 元 正 向 与 整 体 坐 标 系 X 轴 正 向 的 夹 角 大 于 90 ° , 故 其 定 位 向 量 编 号 次 序 为 [ 0 , 0 , 3 , 4 ] , 与 [ 2 , 0 ] 对 应 的 [ 3 , 4 , 0 , 0 ] 相 反 。 注意:1)单元正向逆时针旋转到整体坐标系X轴正向,旋转角不得大于\pi,这必须满足\\ \qquad\quad2)当单元正向与整体坐标系X轴正向的夹角小于90°时,\\ \qquad\quad定位向量编号次序与elemNode单元节点次序一致,\\ \qquad\quad3)当单元正向与整体坐标系X轴正向的夹角大于90°时,\\ \qquad\quad定位向量编号次序与elemNode单元节点次序相反,\\ 所以lambda\_k第四行单元节点次序为[2,0],\\ 但是其单元正向与整体坐标系X轴正向的夹角大于90°,\\ 故其定位向量编号次序为[0,0,3,4],与[2,0]对应的[3,4,0,0]相反。 注意:1)单元正向逆时针旋转到整体坐标系X轴正向,旋转角不得大于π,这必须满足2)当单元正向与整体坐标系X轴正向的夹角小于90°时,定位向量编号次序与elemNode单元节点次序一致,3)当单元正向与整体坐标系X轴正向的夹角大于90°时,定位向量编号次序与elemNode单元节点次序相反,所以lambda_k第四行单元节点次序为[2,0],但是其单元正向与整体坐标系X轴正向的夹角大于90°,故其定位向量编号次序为[0,0,3,4],与[2,0]对应的[3,4,0,0]相反。
nodeCoord = np.array([[0,-2],[0,0],[2,0],[3.5,-2]])
elemNode = np.array([[1,0],[1,2],[2,3],[2,0],[1,3]])
lambda_k =np.array([[0,0,1,2],
[1,2,3,4],
[3,4,0,0],
[0,0,3,4],
[1,2,0,0]])
Forces = np.array([10,10,0,0])
nodeCoord = np.array([[0,-2],[0,0],[2,0],[3.5,-2],[1,-2]])
elemNode = np.array([[1,0],[1,2],[2,3],[2,0],[1,3],[2,4]])
lambda_k =np.array([[0,0,1,2],
[1,2,3,4],
[3,4,0,0],
[0,0,3,4],
[1,2,0,0],
[0,0,3,4]])
Forces = np.array([10,10,0,0])
nodeX = nodeCoord[:,0]
nodeY = nodeCoord[:,1]
k_eL = EA*np.array([
[1,0,-1,0],
[0,0,0,0],
[-1,0,1,0],
[0,0,0,0]
])
def TransMatrix(angle):
return np.array([
[ cos(angle), sin(angle) , 0 , 0 ],
[-sin(angle), cos(angle), 0 , 0 ],
[ 0 , 0 , cos(angle), sin(angle)],
[ 0 , 0 ,-sin(angle), cos(angle)]
])
def K_e(i):
nodeIndex = elemNode[i,:]
node_X1_loc = nodeX[nodeIndex[0]]
node_Y1_loc = nodeY[nodeIndex[0]]
node_X2_loc = nodeX[nodeIndex[1]]
node_Y2_loc = nodeY[nodeIndex[1]]
L = sqrt((node_X2_loc - node_X1_loc) ** 2 + (node_Y2_loc - node_Y1_loc) ** 2)
angle = acos((node_X2_loc-node_X1_loc)/L)
k_e = k_eL / L
return np.matmul(np.matmul((TransMatrix(angle).T) , k_e),TransMatrix(angle))
for i in range(len(elemNode)):
print('')
print('K_e(%d) = '%i ,'\n', K_e(i))
numberOfDof = 2 * len(nodeCoord)
numberOfNodeFreeDof = np.max(lambda_k)
KK = np.zeros((numberOfNodeFreeDof,numberOfNodeFreeDof))
for i in range(len(elemNode)):
for j in lambda_k[i,:]:
if j != 0:
loc_kej = np.argwhere(lambda_k[i, :] == j)
for k in lambda_k[i,:]:
if k != 0:
loc_kek = np.argwhere(lambda_k[i, :] == k)
KK[j-1,k-1] += K_e(i)[loc_kej,loc_kek]
print('='*20)
print('KK = ','\n',KK)
displacement = np.linalg.inv(KK).dot(Forces)
print('\n','displacement:','\n',displacement)
a_e = np.zeros((lambda_k.shape),dtype=float)
a_e += lambda_k
print(a_e)
for i in range(len(elemNode)):
NoZeroIndex_raw = np.argwhere(lambda_k[i, :] != 0)
NoZeroNum = NoZeroIndex_raw.shape[0] * NoZeroIndex_raw.shape[1]
NoZeroIndex = NoZeroIndex_raw.reshape(1, NoZeroNum)
for j in range(NoZeroNum):
indexDof = int(a_e[i,:][NoZeroIndex[0,j]])-1
a_e[i, :][NoZeroIndex[0, j]] = displacement[indexDof]
print(a_e[i,:].shape)
print(a_e)
for i in range(len(elemNode)):
AxialForceXY[i, :] = np.matmul(K_e(i), a_e[i, :])
print('AxialForceXY','\n',AxialForceXY)
2
2.1 apdl命令流
finish
/clear
/prep7
k,1,0,-2,0
k,2,0,0,0
k,3,2,0,0
k,4,3.5,-2,0
k,5,1,-2,0
l,1,2
l,2,3
l,3,4
l,1,3
l,2,4
l,3,5!二次超静定这行保留,
ET,1,LINK1
R,1,4532
MP,EX,1,1/4532
MP,PRXY,1,0.3
LATT,1,1,1
LESIZE,ALL,,,1
LMESH,ALL
DK,1,UX,,,,UY
DK,4,UX,,,,UY
!DK,4,UY
DK,5,UX,,,,UY!约束可自行设置
FORCES = 10
FK,2,FX,FORCES
FK,2,FY,-FORCES
/SOLU
ANTYPE,0
SOLVE
FINISH
静 定 结 构 ( 很 惊 讶 滑 动 铰 支 座 水 平 位 移 如 此 之 大 ! ) 静定结构(很惊讶滑动铰支座水平位移如此之大!) 静定结构(很惊讶滑动铰支座水平位移如此之大!)
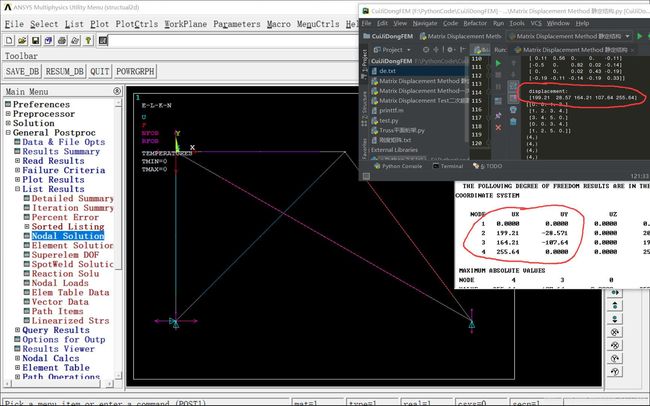
一 次 超 静 定 一次超静定 一次超静定
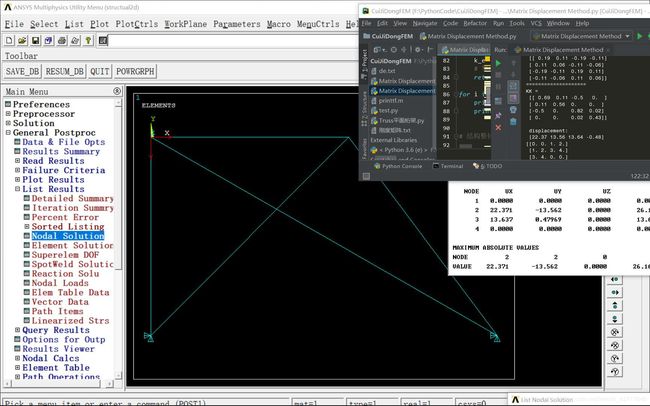
二 次 超 静 定 二次超静定 二次超静定
 哈 哈 , 数 据 基 本 上 是 吻 合 的 … … 哈哈,数据基本上是吻合的…… 哈哈,数据基本上是吻合的……
哈 哈 , 数 据 基 本 上 是 吻 合 的 … … 哈哈,数据基本上是吻合的…… 哈哈,数据基本上是吻合的……

 哈 哈 , 数 据 基 本 上 是 吻 合 的 … … 哈哈,数据基本上是吻合的…… 哈哈,数据基本上是吻合的……
哈 哈 , 数 据 基 本 上 是 吻 合 的 … … 哈哈,数据基本上是吻合的…… 哈哈,数据基本上是吻合的……
