关系模式设计优化（数据库学习重点，难点）

关系模型潜在的问题
1.添加异常（当在关系中添加数据时可能会导致数据的不一致）
2.修改异常（随意的修改关系中的一行记录也可能导致数据的不一致）
3.删除异常（当删除一定数量的记录时可能会导致一些其他信息的丢失）
4.数据冗余（主要是关系中存在了相互之间的约束依赖，使得某一属性的值确定后，另一个属性的值也就确定了）
坏关系
当关系中存在约束，特别是函数依赖，导致冗余，异常等发生就是一个坏关系，如果存在这些问题就需要对关系模式进行优化，而主要的优化技术就是“模式分解”。

第一范式 第二范式 第三范式 BCNF范式–详解连接

函数依赖

函数依赖 （FD）：可形式化表示为：X→Y,其中X和Y是属性集（读为：X决定Y或者Y依赖于X）。即关系R中给定两个元组，如果X属性值相等，则Y的值也必须相等。

函数依赖的作用：函数依赖起到检测冗余是否存在的作用，通过冗余的检测，就能很容易判断出这个关系是不是存在相应的插入，删除，更新异常。

函数依赖集（F）：由关系上一些函数依赖组成的集合叫函数依赖集

函数依赖集的闭包（F+）：由函数依赖集F所蕴含的所有函数依赖的集合

函数依赖和关系的键给定关系R(A,B,C),A→ABC表示A属性决定了R的所有属性，A决定了R，X→R意味着X是一个超键。
超码、候选码、主码 与 外码

不管是判断关系的好坏还是范式的分解都离不开函数依赖，Armstrong公理能够帮助我们从一个给定的函数依赖集推导出它所蕴含的所有的函数依赖。

Armstrong公理（X，Y，Z是属性集）
自反律：若 α为一属性集且 β ⊆ α，则 α→β成立。（比如CD→C，CD→D）
增补律：若α→β成立且γ为一属性集，则γα→γβ成立。
传递律：若α→β和 β→γ成立，则 α→γ成立。
Armstrong公理的重要推论
合并律：若 α→β和 α→γ成立，则α→βγ成立。
分解律：若 α→β成立，则α→β 和α→γ成立。
伪传递律：若α→β和 γβ→δ成立，αγ→δ则成立。
使用Armstrong公理计算F+

属性集闭包

属性集闭包定义
令α为一个属性集。我们将函数依赖集 F 下被α函数确定的所有属性的集合，称为 F 下α的 闭包，记为α+。
属性集闭包的求解
求 A+：将 A 置入 A+。对每一 FD，若左部属于 A+，则将右部置入 A+，一直重复至 A+不能扩大。

属性集闭包的作用
1.判断α是否为超键（即α决定R中的所有属性）：计算α+，检查α+是否包含R 中的所有属性。
2.判断函数依赖α→β是否成立：检查是否有β⊆α+ 。
3.计算函数依赖集的闭包F+：对任意γ⊆ R，找出其属性闭包γ+，对任意的S⊆γ+，输出一个函数依赖γ→S。

通过属性集闭包求函数依赖集F+的例子
已知 F={A→B, B→C },求 F+
第一步：构建一个空的二维表，行和列分别列处所有可能的属性组合

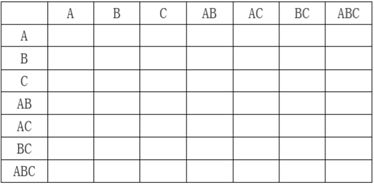
第二步：计算所有属性组合的属性集闭包
已A+为例：
已知 F={A→B, B→C },求 A+
A+ = A
考虑 A→B,A+ = AB
考虑 B→C,B 在 A+中,A+ = ABC
所以可求：A+= ABC ，同理可求

第三步：将包括在对应属性闭包里的属性都勾选出来

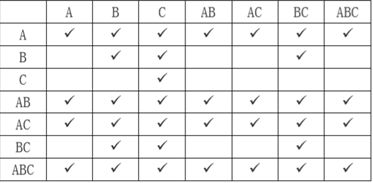
任何一个勾都表示一个函数依赖，比如第一行第六列这个勾表示A→BC（A决定BC）的函数依赖，所有的函数依赖关系组成了函数依赖集的闭包。

模式分解

模式分解的基本标准
1.无损连接分解（如果将R分解为R1和R2，应该满足分解后的两个关系实例能够通过连接组合为原来的关系，使信息不发生改变）

满足条件：
若R分解为R1和R2是无损分解，则下面至少一个成立的话，那么分解就是无损分解：
R1∩R2→R1(函数依赖)
R1∩R2→R2(函数依赖)
实际上将R分解为（UV）和（R-V），如果U→V在R上成立，那么分解时无损连接分解。
2.保持函数依赖
保持函数依赖的分解（直观上）就是R分解为X，Y，Z，函数依赖集（FDs）F在X，Y，Z上成立，那么FDs也会在R上成立。直观上无法在分解后的单一关系上验证原关系上的函数依赖，就表示无法保持函数依赖。

BCNF范式和第三范式

BCNF范式

对于R有函数依赖集F，如果R符合BCNF当且仅当每一个非平凡的FD满足：
1.对于每一个非平凡函数依赖X→Y中，X是R的超键（即X能决定R中的所有属性，所有非平凡函数依赖集F中的箭头左边是键）
2.函数依赖是平凡的（X→Y且Y是X的子集就是平凡函数依赖）

性质
如果R（A，B）只有两个属性，那么它符合BCNF（因为A，B的关系：１.AB之间没有相互一个依赖的关系２.A决定B３.B决定A，第一种情况是平凡函数依赖，第二种A是主键，第三种B是主键，箭头的左边都是我们的键，所以只要关系是两个属性的必然满足BCNF范式）

BCNF范式分解
当一个关系不符合BCNF：那么分解它时考虑到关系R和函数依赖集F，如果F中的函数依赖X→A违背BCNF，那么分解R为R-A和XA，重复这个操作就可以得到一个符合BCNF的关系集合。
BCNF分解一定是保持无损连接分解，通常情况下有多个函数违背BCNF，那么我们处理它们的顺序不同会导致分解的结果不同，得到不同的都符合BCNF的关系集。BCNF范式分解是符合函数依赖的，但是可能不满足保持函数依赖，有的也可能满足保持函数依赖。
例题：
关系模式 R,有U={A,B,C,D,E,G},F={B→G,CE→B,C→A,CE→G,B→D,C→D}
1.候选键
因为 B+ =(B,D,G)；C+=(A,C,D)；CE+=(A,B,C,D,E,G) 所以可知其候选码为 CE
2. 违反 BCNF 的函数依赖：C→A，B→G，B→D,C→D
3. 分解
1）R1={AC};F1={C→A}
R1’={BCDEG};F1’={B→G,CE→B,CE→G,B→D,C→D}；不满足 BCNF
2）R2={BG};F2={B→G} R2’={BCDE};F2’={CE→B,B→D,C→D}；不满足 BCNF
3）R3={BD};F3={B→D}R3’={BCE};F3’={CE→B}；

满足 BCNF 最终答案：R1={AC};R2={BG};R3={BD};R4={BCE};

3NF（三范式）

BCNF范式在有些情况是不能保持函数依赖的，而在更新上有效的检查函数依赖是否违背是很重要的，在BCNF范式的基础上将限制放松一点，从而让分解后的关系保持函数依赖，定义一个弱的关系—3NF。

R符合BCNF，那么R符合３NF，如果R符合3NF，可能存在一定的冗余，它是分解和性能的一种折中。3NF中函数依赖是否保持可以在单独的关系上检查，而不需要进行连接计算，3NF一般是保持无损连接分解和保持函数依赖的。

函数依赖集F符合3NF，当且仅当F中每一个函数依赖X→A（X⊆R and A⊆R）
符合下列描述中的一个：
1.A⊆X（平凡的FD）
2.X是超键
3.A是R的键的一部分

3NF分解

首先第一步是要计算正则覆盖Fc,然后将Fc中每一个函数依赖左右两边属性组合为一个新的关系Ri,再然后判断Ri是否包括R的某个候选键，如果没有包括，则将R的一个候选键属性集单独作为一个新的关系，最后判断一下所有的新关系是否有包含关系，如果有则合并。
例题1：
设有关系模式：R={A,B,C,G,H,I}
函数依赖集F={A→B A→C CG→H CG→I B→H},R如何“双保持”分解为一组3NF？（双保持：无损分解，函数依赖）
第一步：求F的正则覆盖（用合并律）
Fc={A→BC CG→HI B→H}
由于去掉任何属性都和原来的F不等价，所以没有多余的属性。
第二步：求R的3NF分解
A→BC R1=(A,B,C) F1={A→BC}
CG→HI R2=(CGHI) F2={CG→HI}
B→H R3={BH} F3={B→H}
第三步：确定是否添加R候选键做成的子模式
仅一个候选键AG
因为：(AG)+=AGBCHI
而：A+=ABCH G+=G
因该候选键未包含在R1，R2，R3中，需要产生子模式R4=(AG) F4=Ø

例题2
关系cust_bancker_branch(customer_id,employee_id,branch_name,type)
函数依赖集为
F={customer_id,employee_id->branch_name,type
employee_id->branch_name
customer_id,branch_name->employee_id}
首先计算函数依赖集的正则覆盖Fc，branch_name是多余的属性
Fc={customer_id,employee_id->type
employee_id->branch_name
customer_id,branch_name->employee_id}
然后根据Fc生成3个子模式
R1={customer_id,employee_id,type}
R2={employee_id,branch_name}
R3={customer_id,branch_name,employee_id}
候选键customer_id,employee_id是候选键，并且包括在R1中，因此不需要添加新的关系模式
又因为R3包括R2，因此删除R2得到最终的关系分解结果：
R1={customer_id,employee_id,type}
R3={customer_id,branch_name,employee_id}
例题3
关系模式 R,有 U={A,B,C,D,E,G},F={B→G,CE→B,C→A,CE→G,B→D,C→D}，求3NF分解
0.候选码
因为 B+=(B,D,G)；C+=(A,C,D)；CE+=(A,B,C,D,E,G)
所以可知其候选码为 CE
1.正则覆盖
1）运用算法和定义，可以合并 B→G,B→D 为 B→DG；合并
C→A,C→D 为 C→AD；合并 CE→B,CE→G 为 CE→BG。 得到函数依赖集 FC={B→DG,C→AD,CE→BG}
2) 消除无关属性
验证 G 是 CE→BG 的右方无关属性
FC’={B→DG,C→AD,CE→B}， (CE)FC’+=(CEBDG)，所以 FC’蕴含 FC 的 CE→BG，G 是 CE→BG 的右方无关属性,可以消除 正则覆盖 FC={B→DG,C→AD,CE→B}
2. 由FC={B→DG,C→AD,CE→B}可以分解 R1={BDG},F1={B→DG}
R2={ACD},F2={C→AD} R3={BCE},F3={CE→B}
3.检查 候选键 CE 包含在 R3 中，不需要添加子模式，每个子模式之间无包含关系 最后答案：R1={BDG} ，R2={ACD}，R3={BCE}；

正则覆盖

正则覆盖的定义
函数依赖集F 的正则覆盖 Fc，是 F 的最小函数依赖集，使得 F 与 Fc 相互蕴含。
正则覆盖必须满足的性质
1.Fc中任何函数依赖都不包含无关属性
2.Fc 中函数依赖的左半边都是唯一的
无关属性的定义
如果去除函数依赖中的一个属性，不改变该函数依赖集的闭包，则称该属性是无关的
无关属性的形式化定义
设函数依赖集 F 中有α→β 
1.如果 A∈α并且 F 逻辑蕴含（F – {α→β}）∪{(α- A) →β},则属性 A 在α中是无关的。 
2.如果 A∈β并且函数依赖集( F - { α→β} )∪{ α→( β- A ) }逻辑蕴含 F，则属性 A 在β中是无关的。（A逻辑蕴含B我感觉就是A能够推导出B）

正则覆盖计算过程


例题：
求 F={A→B,B→A,B→C,A→C,C→A},最小函数依赖集合Fc
1、利用分解规则，将所有的函数依赖变成右边都是单个属性的函数依赖
从题目来看，F中的任何一个函数依赖的右部仅含有一个属性{A→B,B→A,B→C,A→C,C→A}
2、去掉F 中多余的函数依赖
(即假设某个依赖冗余，删除该依赖后的函数依赖集中，在删除的依赖关系箭头左边的属性的闭包能够包含箭头右边的属性，说明冗余则删除，否则进行还原,最终得到的最小函数依赖集使用合并律进行合并得到正则覆盖)
（1）设A→B冗余
从F 中去掉A→B,则F1={B→A,B→C,A→C,C→A}。
根据F1 计算A+ =AC,但AC 不包含B，故A->B 不能从Ｆ中去掉。
（2）设B→A冗余从F 中去掉B→A，则F2={A→B,B→C,A→C,C→A}。
根据F2 计算B+ =ABC,包含所有属性，故B→A可从Ｆ中去掉。
（3）设B→C冗余
从F 中去掉B→C，则F3={A→B,A→C,C→A}。
根据F3 计算B+= B,不包含C，故B→C不是冗余的函数依赖，不能从F 中去掉。
（4）设A→C冗余
从F 中去掉A→C，则F4={A→B,B→C，C→A}。
根据F4 计算A+ =ABC，包含所有属性，故A→C可从Ｆ中去掉。
（5）设C→A冗余
从F 中去掉C→A，则F5={A→B,B→C}。
根据F5 计算C+= C 不包含A，故C→A不是冗余的函数依赖，不能从F 中去掉。
（6）至此
所有依赖均以验算完毕，故
F 最小函数依赖集合为：{A→B,B→C，C→A}

BCNF和3NF的比较
将一个关系分解为符合3NF的关系集合：
1.分解是无损的
2.分解是保持函数依赖的
将一个关系分解为符合BCNF的关系集合
1.分解是无损的
2.可能不保持函数依赖

总结

1.若分解无损分解为BCNF，可能不能保存函数依赖，若为保持函数依赖而不分解，可能存在数据冗余现象，各有利弊，需因应用需求而定。数据库优化的过程，一般是首先分解为BCNF
，如果分解成BCNF，发现丢失了重要的函数依赖，则返回到3NF，如果某些多表连接查询也非常重要，则返回到2NF甚至是1NF。
2.范式分解的方法
BCNF分解：
首先需要做的事情是分析关系的函数依赖集F中的函数依赖，找出不符合BCNF的函数依赖，将其箭头左右两端的属性取出，组合成一个新的关系，而从关系R中除掉箭头右端的属性后剩余的属性组成另外一个关系，之后再分析这两个关系是否符合BCNF，如果不符合需要进一步分解。

3NF分解
首先需要做的事情是找出关系的正则覆盖Fc,然后将正则覆盖的每一个函数依赖箭头两端的 属性组合成新的关系，之后检测关系R的候选键是否已经存在于新的关系中，如果没有则将候选键作为新的关系，最后审查一下所有关系，看是否有包含关系，有则合并。