数据结构与算法分析 收获总结 第7章 排序

先以老师上课所讲的经典面试题：
1.把两个排好序的数组，合并为一个数组，第一个数组后半部分刚好可以容纳第一个数组的元素，空间复杂度O(1)
解析：由于空间复杂度要求，所以不可再开一个temp数组之类的方法。

void sort(int Array1[],int n,int Array2[],int m)
{
     int p1=n-1,p2=m+n-1; 
     int t=m-1;
     while(p1!=p2)
     {
         if(p1==-1)
         {
             Array1[p2]=Array2[t];
             break;
         }     
         if(Array2[t]>=Array1[p1])
         Array1[p2--]=Array2[t--];
         else
         {
             Array1[p2--]=Array1[p1--];
         }
     }    

2.假设数组已经排好序，即如果把数组排好序，每个元素移动的距离不超过k，并且k相对于数组长度来说很小，请问选择什么排序法比较好。
3.判断数组中是否有重复值，空间复杂度为O(1)
4.荷兰国旗问题，对只包含0,1，2的整数数组进行排序，时间复杂度O(N)，空间复杂度O(1)
解析：三个指针
5.在行和列都排好序的矩阵中找给定的数，时间复杂度O(M+N)
如：

        0 1 2 5
        2 3 4 7
        4 4 4 8
        5 7 7 9

解析：右上角开始，找稍大向下走，找稍小向左走
6.在给定数组中，找到中间需要排序的子数组，时间复杂度O（N）,空间复杂度O(1)
如：1 3 5 6 4 7 2 8 9中子数组5 6 4 7 2需要排序

这一章的重点就是八大排序，根据以往考题，主要考察每个算法的执行过程，思想，方法以及时间（平均，最好，最坏），空间复杂度（辅助空间），以及通过理解每个算法来判断算法的稳定性（直接记住也行），考题里倒是没怎么涉及对每个算法代码的书写。

八大排序详解推荐这个超高阅读量帖子：
https://blog.csdn.net/hguisu/article/details/7776068

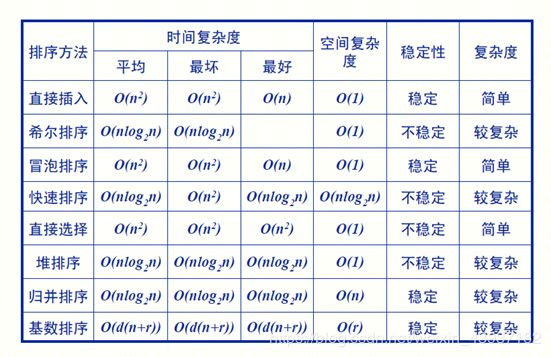
希尔排序的最好时间为n1.3次幂~n1.5次幂
自己的理解:
以下代码来自数据结构与算法分析（第三版）电子工业出版社
1.插入排序：从第二个开始，向之前序列插入当前元素，放在之前序列的正确位置

template<typename E，typename Comp>
void insertionsort(E  A[],int n){
  for(int i=1;i<=n;i++)  //插入第i个元素
    for(int j=i;(j>0)&&(Comp::prior(A[j],A[j-1]));j--)
      swap(A,j,j-1)l
}

2.希尔排序：折半，增量为n/2,n/4,n/8,…1，每一轮都间隔增量的元素进行比较并排序

template<typename E，typename Comp>
void inssort2(E A[],int n,int incr){
  for (int i=incr;i<n;i+= incr){  //对每一个增量制定的序列，从开头开始排序（进行下一个for循环），直到最后一个元素。保证该增量对应的序列有序
   for(int j=i;(j>=incr)&&(Comp::prior(A[j],A[j-incr]));j-=incr) //元素与前一个增量元素比较，如果确定小于，则减去增量并交换，再与前一个增量比较
     swap(A,j,j-incr);
           }
     }
     
template<typename E，typename Comp>
void shellsort(E A[],int n){
   for(int i=n/2;i>2;i/=2)  //对于每个增量increment从n/2开始，直到1
     for(int j=0;j<i;j++)
        inssort2<E,Comp>(&A[j],n-j,i);  //此时的n-j因为最后j个不需考虑，会通过前面进行排序的
     inssort2<E,Comp>(A,n,1);//增量为1时再进行一次排序（此时序列已经较整齐了）
}

3.冒泡排序：不断将每一轮最大值沉到底

template<typename E，typename Comp>
void bubblesort(E  A[],int n){
    for(int i=1;i<n-1;i++)  //向上冒泡，将较小的向上拿
      for(int j=n-1;j>i;j--)
        if(Comp::prior(A[j],A[j-1]))
           swap(A,j,j-1);
}

4.快速排序：选取标兵（开头/结尾）(轴值pivot)，统计比它大，比它小的，然后直接将它置于正确的位置，再对前后两序列再进行快排
推荐：https://blog.csdn.net/qq_36528114/article/details/78667034

void QuickSort(int* array,int left,int right)
{
	assert(array);
	if(left >= right)//表示已经完成一个组
	{
		return;
	}
	int index = PartSort(array,left,right);//枢轴的位置
	QuickSort(array,left,index - 1);
	QuickSort(array,index + 1,right);
}

5.选择排序：选择最大的置于n,在剩下的选择最大的置于n-1…

template<typename E，typename Comp>
void selectionsort(E  A[],int n){
  for(int i=0;i<n-1;i++){
      int lowindex=i;  //第lowindex小
      for(int j=n-1;j>i;j--)   //从最后向前搜索，直到到达i，因为i前都已经处于正确位置
        if(Comp::prior(A[j],A[lowindex]))  //（A[j]应该在A[lowindex]之前）
           lowindex = j;   //lowindex记录当前搜索的可能是第lowindex小的数的下标
        swap(A,i,lowindex);//前面for循环结束后，已找到第i小的元素，下标即为lowindex，交换后置于正确位置
      }
  }

6.堆排序：建堆，取堆顶元素（最大）于数组后（用于记录），再重建堆，再取堆顶（即第n-1大数）于数组后

template<typename E，typename Comp>
void heapsort(E A[],int n){
  E maxval;   //记录每次的最大值（堆顶）
  heap<E,Comp>H(A,n,n);  //建堆
  for (int i=0;i<n;i++)   
     maxval = H.removefirst();//取出maxval并放在最后
}

7.归并排序：先两两长度为1数并比较并排序，再两两长度为2序列比较并排序，…=>直到两个长度n/2，比较排序=>最终序列
递归实现:

template<typename E，typename Comp>
void mergesort(E  A[],E temp[],int left, int right){
  if((right->left)<=threshold){   //small list
     insertionsort<E,Comp>(&A[left],right-left+1);
     return;
     }
  int i,j,k,mid=(left+right)/2;
  mergesort<E,Comp>(A,temp,left,mid);
  mergesort<E,Comp>(A,temp,mid+1,right);
 //进行归并操作。第一，复制两个一半作为临时
  for(i=mid;i>=left;i--) temp[i]=A[i];
  for(j=1;j<=right-mid;j++)temp[right-j+1]=A[j+mid]; 
 //合并子表sublist作为A
  for(i=left,j=right,k=left;k<=right;k++)
     if(Comp::prior(temp[i],temp[j])) A[k]=temp[i++];
     else A[k] = temp[j--];
}

8.基数排序：桶式排序，第一轮个位放桶中，使个位有序；第二轮十位放个位，使十位有序，…（桶中先进先出）
https://blog.csdn.net/zhen921/article/details/80354096
https://blog.csdn.net/atskyline/article/details/7075333