AVL定义:
AVL的命名是由2个其发明者的名字组成的,G.M.Adelson-Velsky和E.M.Landis,两个俄罗斯人。AVL既有平衡二叉树的特性,又有二分搜索树的特性。
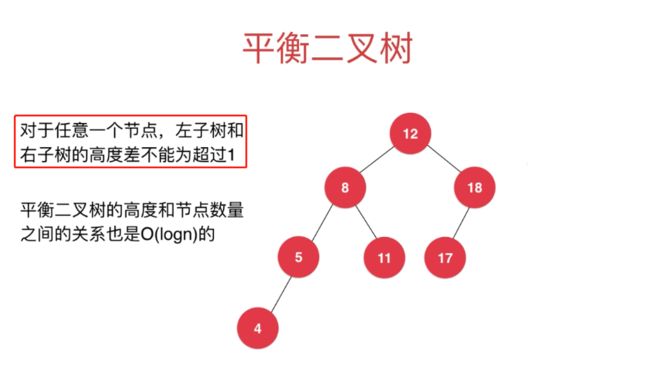
平衡二叉树:对于任意一个节点,左子树和右子树的高度差不能超过1。
二分搜索树:
1、二分搜索树的每个节点的值,大于其左子树的所有节点的值;小于其右子树的所有节点的值;
2、每一颗子树也是二分搜索树。
AVL结构:
因为AVL是二分搜索树,所以可以直接使用其结构,这里泛型使用了映射(Map),是为了符合更多的数据类型。然后新增了变量height,来表示当前节点的高度,其中叶子节点的高度为1。如下图:
public class AVLTree, V>{
private class Node{
//当前节点的值
public K key;
public V value;
//左节点
public Node left;
//右节点
public Node right;
// 节点高度,叶子结点为1
public int height;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
height = 1;
}
}
private Node root;
private int size;
获取节点的高度和平衡因子:
平衡因子:左孩子的高度减去右孩子的高度。
1、获取当前节点的高度:
// 获取节点node的高度
private int getHeight(Node node){
if (node == null) return 0;
return node.height;
}
2、获取当前节点的平衡因子:
// 获取节点node的平衡因子,平衡因子不在[-1,1]区间,说明不是平衡二叉树
private int getBalanceFactory(Node node){
if (node == null) return 0;
return getHeight(node.left) - getHeight(node.right);
}
判断该二叉树是否是一颗二分搜索树:
思路:因为二分搜索树的中序遍历会使元素自然排序,于是我们可以利用这个特性。对当前的二叉树进行中序遍历,把值存入一个集合List中,然后遍历这个List,看前一个元素是否小于后一个元素,如果有一个不满足返回false,直到全部元素遍历完才返回true。
// 判断该二叉树是否是一颗二分搜索树
public boolean isBST(){
// 二分搜索树的一个特性:中序遍历的结果是自然排序的
ArrayList keys = new ArrayList<>();
inOrder(root, keys);
for (int i = 1; i < keys.size(); i++) {
if (keys.get(i - 1).compareTo(keys.get(i)) > 0)
return false;
}
return true;
}
// 中序遍历
private void inOrder(Node node, ArrayList keys) {
if (node == null) return;
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right, keys);
}
判断该二叉树是否是一颗平衡二叉树:
思路:遍历判断当前节点的平衡因子balanceFactory是否 > 1,递归的终止条件为:1、执行到最后一个NULL元素,此时平衡因子为0,返回true;2、平衡因子>1,返回false。递归执行,只有左右孩子同时满足平衡二叉树的特性时才为true。
// 判断该二叉树是否是一颗平衡二叉树,看平衡因子
public boolean isBalanced(){
return isBalanced(root);
}
// 判断node为根的二叉树是否是一颗平衡二叉树,递归算法
private boolean isBalanced(Node node) {
if (node == null) return true;
int balanceFactory = getBalanceFactory(node);
if (Math.abs(balanceFactory) > 1)
return false;
// 左右子树递归都为true才行
return isBalanced(node.left) && isBalanced(node.right);
}
LL与AVL的右旋转:
在执行了添加元素或者删除元素之后,由于会对节点高度进行修改,很可能破坏AVL的平衡性。于是需要左旋转或者右旋转操作来使AVL重新获得平衡。
右旋转的时机:插入的元素在不平衡节点的左侧的左侧(LL)。
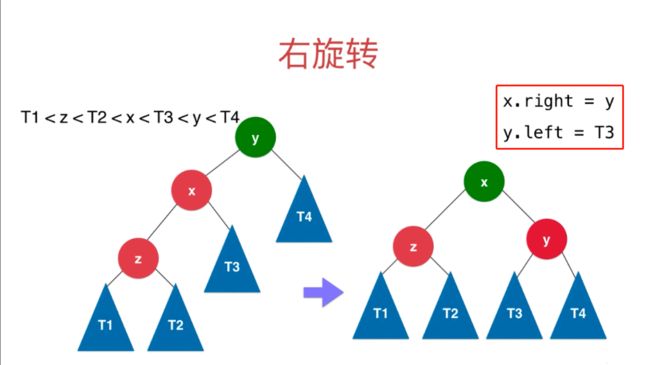
我们先看右旋转,如下图:
首先从新增或者删除的元素往上,找到第一个平衡因子=2的节点,如上图的 y,然后取出 x 的右子树 T3,然后使 y 的左子树 x 的右孩子指向 y,然后让 y 的左子树指向 T3。此时 x 成为了新的AVL的根节点,并且新的AVL即符合平衡二叉树的特性又符合二分搜索树的特性。
右旋转代码实现:
// 对节点y进行向右旋转操作,返回旋转后新的根节点x
// y x
// / \ / \
// x T4 向右旋转 (y) z y
// / \ - - - - - - - -> / \ / \
// z T3 T1 T2 T3 T4
// / \
// T1 T2
private Node rightRotate(Node y){
// 取出y 的左孩子x的右孩子T3
Node x = y.left;
Node T3 = x.right;
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
RR与AVL的左旋转:
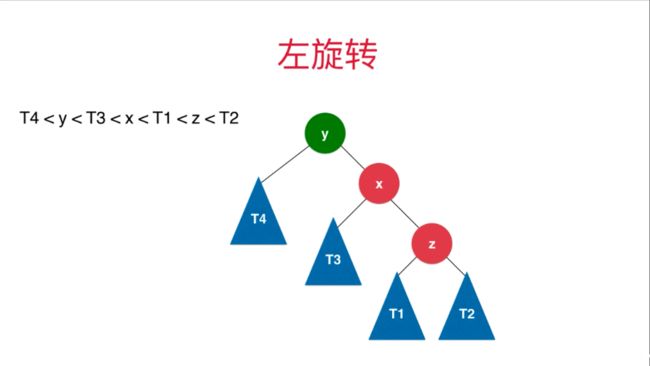
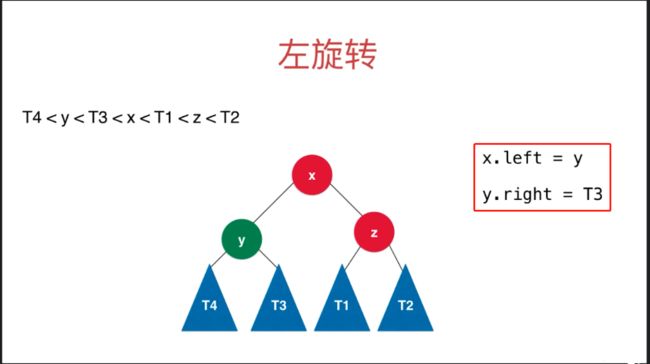
左旋转和右旋转刚好相反,于是实现机制是一样的。
左旋转的时机: 插入的元素在不平衡节点的右侧的右侧(RR)。
左旋转的代码实现:
// 对节点y进行向左旋转操作,返回旋转后新的根节点x
// y x
// / \ / \
// T4 x 向左旋转 (y) y z
// / \ - - - - - - - -> / \ / \
// T3 z T4 T3 T1 T2
// / \
// T1 T2
private Node leftRotate(Node y){
// 取出y 的右孩子x的左孩子T3
Node x = y.right;
Node T3 = x.left;
x.left = y;
y.right = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
LR:
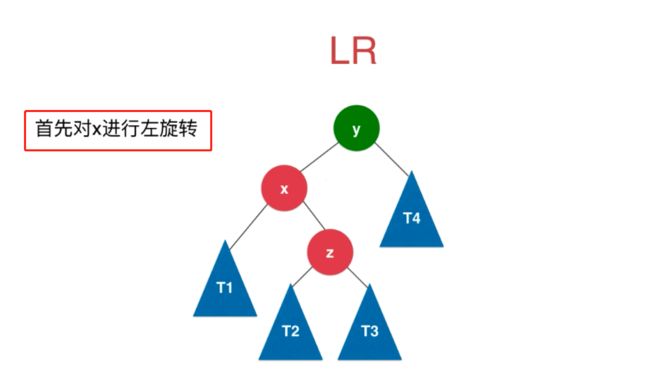
插入的元素在不平衡节点的左侧的右侧(LR)。
此时则需要让不平衡节点 y 的左孩子 x 进行左旋转,然后让不平衡节点 y 的左子树指向左旋转之后的新的二叉树的根节点 z。如下图:
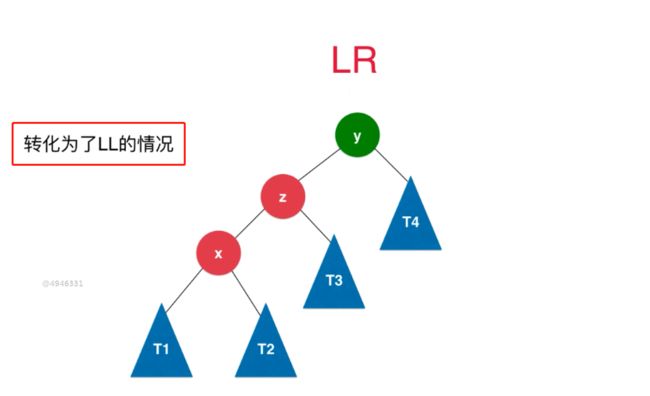
此时,已经俨然成为了LL的情况,于是 y 节点右旋转就解决了啦。
RL:
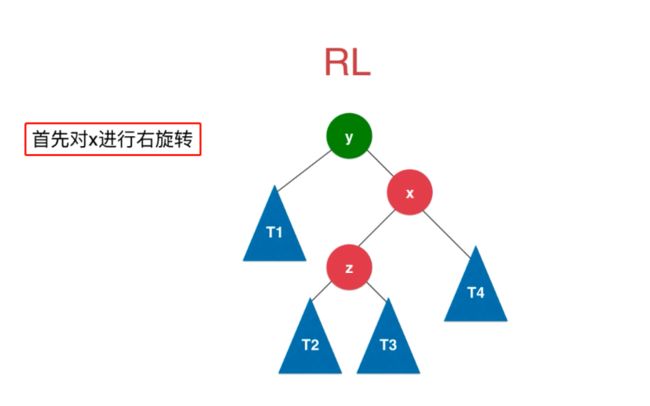
插入的元素在不平衡节点的右侧的左侧(RL)。
此时则需要让不平衡节点 y 的右孩子 x 进行右旋转,然后让不平衡节点 y 的右子树指向右旋转之后的新的二叉树的根节点 z。如下图:
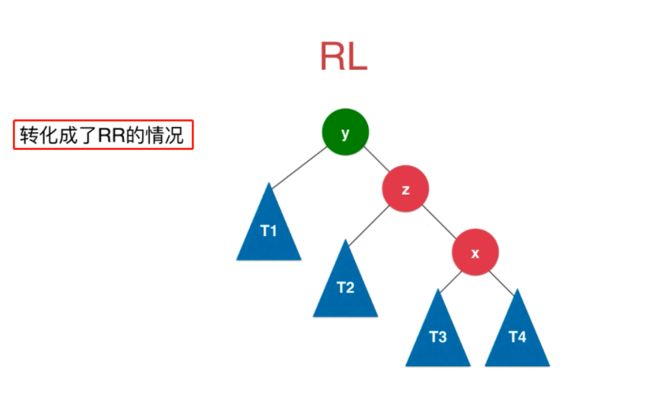
此时,已经俨然成为了RR的情况,于是 y 节点左旋转就解决了啦。
添加元素:
递归操作,递归的终止条件:当前节点为NULL,表示到达最后一个根节点NULL,则将新节点放入该位置。然后比较所给的key与当前node节点的key的大小,如果小于,则新增的节点放在左子树,于是往左子树递归;反之,往右子树递归;当二者相等时,则更新value值。然后更新node的height,计算node的平衡因子,如果平衡因子的绝对值 <= 1,则表示符合AVL特性,直接返回node;否则,就是已经破坏了AVL的平衡性,需要根据不同情况来进行左右旋转。
public void add(K key, V value) {
root = add(root, key, value);
}
// 向 node 为根的二分搜索树中添加新的元素(key, value)
// 返回插入新节点后的二分搜索树的根
private Node add(Node node, K key, V value) {
//递归终止条件
if (node == null) {
//表示到达最后一个根节点null,则将新节点放入该位置
size++;
return new Node(key, value);
}
if (key.compareTo(node.key) < 0){
//递归步骤,往往递归终止条件的参数是和递归步骤的参数对应的
//将插入新节点后的二分搜索树的根挂在当前树上
node.left = add(node.left, key, value);
}else if(key.compareTo(node.key) > 0){
node.right = add(node.right, key, value);
}else {
// 更新value值
node.value = value;
}
// 更新 height,左右孩子中大的height + 1
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
// 计算平衡因子
int balanceFactory = getBalanceFactory(node);
if (Math.abs(balanceFactory) <= 1) return node;
// 不符合平衡二叉树条件,需要平衡维护
if (balanceFactory > 1){
if (getBalanceFactory(node.left) >= 0){
// 插入的元素在不平衡节点的左侧的左侧(LL),采用右旋转
return rightRotate(node);
}else{
// 插入的元素在不平衡节点的左侧的右侧(LR),采用先左旋转再右旋转
node.left = leftRotate(node.left);
return rightRotate(node);
}
}
if (balanceFactory < -1){
if (getBalanceFactory(node.right) <= 0){
// 插入的元素在不平衡节点的右侧的右侧(RR),采用左旋转
return leftRotate(node);
}else {
// 插入的元素在不平衡节点的右侧的左侧(RL),采用右旋转再左旋转
node.right = rightRotate(node.right);
return leftRotate(node);
}
}
return node;
}
删除元素:
思路:依旧是递归执行,递归的终止条件:1、走到最后没有找到 key;2、找到key,即node.key.compareTo(key) == 0,此时也要分情况考虑,当左子树为空,则把右子树的根节点作为新二叉树的根节点,然后将node的右子树置为NULL,让GC回收;同理,右子树为空时,则把左子树的根节点作为新二叉树的根节点,然后将node的左子树置为NULL;当左右子树都不为空时,则找出右子树的最小值 successor 用来顶替待删除节点的位置(后继策略)。最后还是需要对上述操作之后返回的retNode进行平衡因子的判断,如果失去了平衡性,则需要根据不同情况进行左右旋转。
public V remove(K key) {
Node node = getNode(root, key);
if (node != null) {
root = remove(root, key);
return node.value;
}
return null;
}
// 删除以node为根的二分搜索树中的键为key的节点
// 返回删除节点后的新的二分搜索树
private Node remove(Node node, K key) {
// 递归终止条件: 1、走到最后没有找到key ; 2、找到key
if (node == null) return node;
Node retNode;
if (node.key.compareTo(key) == 0){
if (node.left == null){
// 待删除的节点左子树为空的情况
Node rightNode = node.right;
node.right = null;
size--;
retNode = rightNode;
} else if (node.right == null){
// 待删除的节点右子树为空的情况
Node leftNode = node.left;
node.left = null;
size--;
retNode = leftNode;
}else {
// 左右子树都不为空,则找出右子树的最小值,即采用e 的后继。然后用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
//由于removeMin 并未对删除元素之后进行平衡检查,所以要么加上,要不不用;
// 我们这里采用不用,直接使用remove,因为successor就是node.right子树的最小值
// successor.right = removeMin(node.right);
successor.right = remove(node.right, successor.key);
successor.left = node.left;
node.left = null;
node.right = null;
//注意:这里不需要size--,因为removeMin(node.right) 已经操作了size--
retNode = successor;
}
}else if (key.compareTo(node.key) < 0){
node.left = remove(node.left, key);
retNode = node;
}else {
node.right = remove(node.right, key);
retNode = node;
}
if (retNode == null) return retNode;
// 更新 height,左右孩子中大的height + 1
retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
// 计算平衡因子
int balanceFactory = getBalanceFactory(retNode);
// 不符合平衡二叉树条件,需要平衡维护
if (balanceFactory > 1){
if (getBalanceFactory(retNode.left) >= 0){
// 插入的元素在不平衡节点的左侧的左侧(LL),采用右旋转
return rightRotate(retNode);
}else{
// 插入的元素在不平衡节点的左侧的右侧(LR),采用先左旋转再右旋转
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
}
if (balanceFactory < -1){
if (getBalanceFactory(retNode.right) <= 0){
// 插入的元素在不平衡节点的右侧的右侧(RR),采用左旋转
return leftRotate(retNode);
}else {
// 插入的元素在不平衡节点的右侧的左侧(RL),采用右旋转再左旋转
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
}
return retNode;
}
小结:
至此,AVL的基本操作已经介绍完了,由于它不会像二分搜索树那样退化成链表,所以它的添加元素和删除元素的时间复杂度都是O(log n)。