推荐系统——Item2vec

一、背景

推荐系统中，传统的CF算法都是利用 item2item 关系计算商品间相似性。i2i数据在业界的推荐系统中起着非常重要的作用。传统的i2i的主要计算方法分两类，memory-based和model-based。

本文主要介绍了microsoft和airbnb两大公司如何将embedding技术应用于推荐／搜索业务。实践证明，embedding技术对于工业场景来说有着很大的价值和应用前景。

还有什么是 embedding？为什么说 embedding 是深度学习的基本操作？

简单来说，embedding 就是用一个低维的向量表示一个物体，可以是一个词，或是一个商品，或是一个电影等等。这个 embedding 向量的性质是能使距离相近的向量对应的物体有相近的含义，比如 Embedding(复仇者联盟)和 Embedding(钢铁侠)之间的距离就会很接近，但 Embedding(复仇者联盟)和 Embedding(乱世佳人)的距离就会远一些。

除此之外 Embedding 甚至还具有数学运算的关系，比如 Embedding（马德里）-Embedding（西班牙）+Embedding(法国)≈Embedding(巴黎)

从另外一个空间表达物体，甚至揭示了物体间的潜在关系，从某种意义上来说，Embedding 方法甚至具备了一些本体论的哲学意义。

言归正传，Embedding 能够用低维向量对物体进行编码还能保留其含义的特点非常适合深度学习。在传统机器学习模型构建过程中，我们经常使用 one hot encoding 对离散特征，特别是 id 类特征进行编码，但由于 one hot encoding 的维度等于物体的总数，比如阿里的商品 one hot encoding 的维度就至少是千万量级的。这样的编码方式对于商品来说是极端稀疏的，甚至用 multi hot encoding 对用户浏览历史的编码也会是一个非常稀疏的向量。而深度学习的特点以及工程方面的原因使其不利于稀疏特征向量的处理。因此如果能把物体编码为一个低维稠密向量再喂给 DNN，自然是一个高效的基本操作。

首先先了解一下word2vec,不太清楚朋友可以转补到
NLP–Word2Vec详解

二. Item Embedding

2.1 item2vec Microsoft

ITEM2VEC: NEURAL ITEM EMBEDDING FOR COLLABORATIVE FILTERING

这篇论文是微软将word2vec应用于推荐领域的一篇实用性很强的文章。该文的方法简单易用，可以说极大拓展了word2vec的应用范围，使其从NLP领域直接扩展到推荐、广告、搜索等任何可以生成sequence的领域。

2.1.1 SKip-gram with negative sampling

目标函数

$\frac{1}{K}{\sum }_{i=1}^K{\sum }_{-c\le j\le c,j\ne 0}\log p\left(w_{i+j}|w_i\right)$

其中

$\begin{array}{c}p\left(w_j|w_i\right)=\sigma \left(u_i^T{v}_k\right){\prod }_{k=1}^N\sigma \left(-u_i^T{v}_k\right)\\ \sigma (x)=1/1+\exp (-x)\end{array}$

为了] 对样本进行二次采样, 以一定概率丢弃样本

$p(\mathrm{discard}|w)=1-\sqrt{\frac{\rho }{f(w)}}$

2.1.2 item2vec

item出现在同一集合中为正例，否则为负例。同一集合可以根据具体场景定义，例如：用户同一订单下的商品。

目标函数变更为：

$\frac{1}{K}{\sum }_{i=1}^K{\sum }_{j\ne i}^K\log p\left(w_j|w_i\right)$

2.1.3 Experimental Results
数据集

1. Microsoft Xbox Music

   user-artist relation：用户播放了某个歌手的歌曲

2. Microsoft Store

用户同一订单下订购的商品

结果

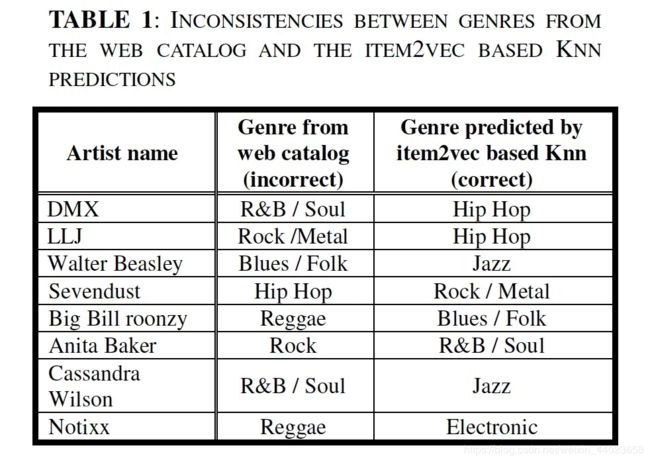
• 将用item2vec方式和SVD方式产出的artist embedding降维到2维空间，如图所示：

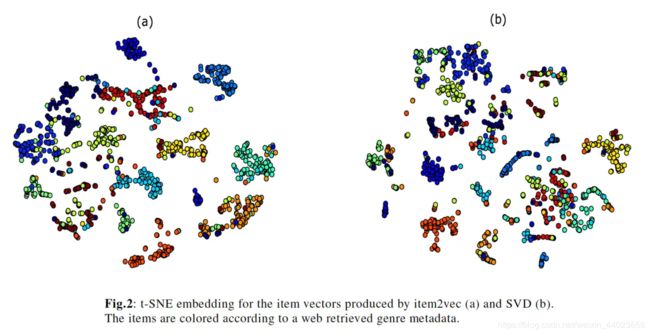并将同种类型的artists用相同颜色进行标识，结果显示，item2vec的聚合效果更好。

• 能够使用简单的KNN方式对网上artists的类型进行纠正和标注
  
  对topq的artists进行分类预测（KNN），准确率较高，且对历史数据较少的artists表示效果更好

• item2vec和SVD直观效果比较，表中列除了seed item以及与其最相似item
  可以得出结论：

1）item2vec可以探索出除了“类型”之外其他的相似性；

2）item2vec提供列更相关的item，且对于信息较少的情况下，表现较佳

2.2 item2vec Airbnb

Real-time Personalization using Embeddings for Search Ranking at Airbnb

Airbnb的这篇论文是KDD 2018的best paper。我们知道，airbnb是全世界最大的短租网站。在平台上，房东(host)可以向用户(user)提供房源(listing)，用户可以通过输入地点、价位等关键词搜索相关的房源信息，并做浏览选择。user和host的交互行为分成三种：user点击／预定listing，host拒绝预定。基于这样的业务背景，本文提出了两种embedding的方法分别去capture用户的短期兴趣和长期兴趣。利用用户click session和booking session序列，训练生成listing embedding 和 user-type&listing-tpye embedding，并将embedding特征输入到搜索场景下的rank模型，提升模型效果。下面会分别介绍这两种embedding方法。

2.2.1 Listing Embedding
数据.

利用用户的click session，定义点击listing序列，并基于此序列训练出listing embedding。

click session定义：用户在一次搜索中点击的listing序列。序列生成有两个限制条件：1) 停留时间超过30s，点击有效 2) 用户点击间隔时间超过30min，记为新序列

模型.

基于负采样的Skip-gram模型结构，并对目标函数进行了改造。

negative sampling方式训练的objective如下，采用随机梯度上升的方法更新参数。

$\underset{\theta }{\mathrm{argmax}}{\sum }_{(l,c)\in {\mathcal{D}}_p}\log \frac{1}{1+e^{-{\mathbf{v}}_c^{\prime }{\mathbf{v}}_l}}+{\sum }_{(l,c)\in {\mathcal{D}}_n}\log \frac{1}{1+e^{{\mathbf{v}}_c^{\prime }{\mathbf{v}}_l}}$

正样本：滑动窗口中的listing；负样本：listing集合中随机采样的样本。

Airbnb基于实际场景，针对业务特点，做了如下改造：

• 引入订购信息，将点击后最终订购的房源作为全局的上下文条件 (global context)，以正样本的形式加入到目标函数：

$\underset{\theta }{\mathrm{argmax}}{\sum }_{(l,c)\in {\mathcal{D}}_p}\log \frac{1}{1+e^{-{\mathrm{v}}_c^{\prime }{\mathrm{v}}_l}}+{\sum }_{(l,c)\in {\mathcal{D}}_n}\log \frac{1}{1+e^{{\mathrm{v}}_c^{\prime }{\mathrm{v}}_l}}+\sqrt{\log \frac{1}{1+e^{-{\mathrm{v}}_l^{\prime }}{\mathrm{v}}_l}}$

即不管这个booking listing是否在滑动窗口内，都会认为它与中心listing相关。直观上也很好理解，即浏览点击的房源和我最终预订目标一定是相似相关的。

• 考虑到线上预订旅行住所，用户搜索浏览的往往是单一地点（目的地）的listing。因此正样本往往都是在同一地点，而随机采样的负样本极有可能不在同一地点，这种不平衡往往会导致学不到最优解。为了更好地发现同一地点房源的差异性，修改目标函数如下：

$\underset{\theta }{\mathrm{argmax}}{\sum }_{(l,c)\in {\mathcal{D}}_p}\log \frac{1}{1+e^{-{\mathbf{v}}_c^{\prime }{\mathbf{v}}_l}}+{\sum }_{(l,c)\in {\mathcal{D}}_n}\log \frac{1}{1+e^{{\mathbf{v}}_c^{\prime }{\mathbf{v}}_l}}$
$+\log \frac{1}{1+e^{-{\mathbf{v}}_l^{\prime },{\mathbf{v}}_l}}+\sqrt{{\sum }_{l,m_n}{\sum }_{{\mathcal{D}}_{m_n}}\log \frac{1}{1+e^{{\mathbf{v}}_{m_n^{\prime }}}}}$

即加入另一组与中心房源地点相同的listing集合中进行随机抽样的negative samples。

此外，文中还提到了listing embedding冷启动问题的解决方法。平台每天都有新房源登记，房东登记房源往往会提供房源的地点、价格等基本信息，取附近的3个同样类型、相似价格的listing embedding平均值生成该房源的embedding，用这种方法可以覆盖98%新房源，不失为一个实用的工程经验。

评估.

生成的listing embedding向量捕捉了怎样的特征？做了如下验证。

基于学到的embedding使用k-means方法聚类，由图下2以看出，相近位置的房源聚集在了一起，embedding向量成功捕捉到房源的位置特征；此外，由表1&2可以看出，相同类型和价格范围的房源之间的余弦相似性远高于不同类型和不同价格的房源之间的相似性。房源类型、价格三类特征已很好地包含在embedding中。

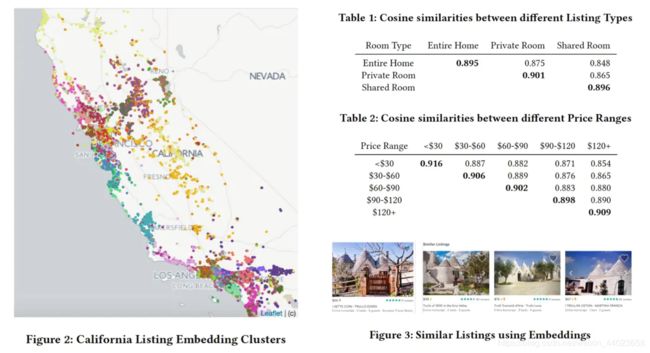
除了像价格这种可以不用学习直接可以拿到的房源信息特征，还有一些无法直接提取到的特征，例如建筑风格、设计风格、感觉等。为了直观上评估embedding的效果，Airbub做了一个验证工具，根据输入listing输出K个最近邻listings，由图中可以看出返回的房源建筑风格与目标房源有着相同的建筑风格。

2.2.2 User-type & Listing-type Embedding
点击行为可以反映用户的实时需求，但往往无法捕捉用户长期兴趣偏好。

使用booking session序列来捕捉用户长期兴趣，但是这里会遇到严重的数据稀疏问题。

数据.

booking session的数据稀疏问题

• book行为的数量远远小于click的行为
• 单一用户的book行为很少，大量用户在过去一年甚至只book过一个房源
• 大部分listing被book的次数较少

如何解决这些问题？利用User-type&Listing-type进行聚合。用户和房源属性如下表。

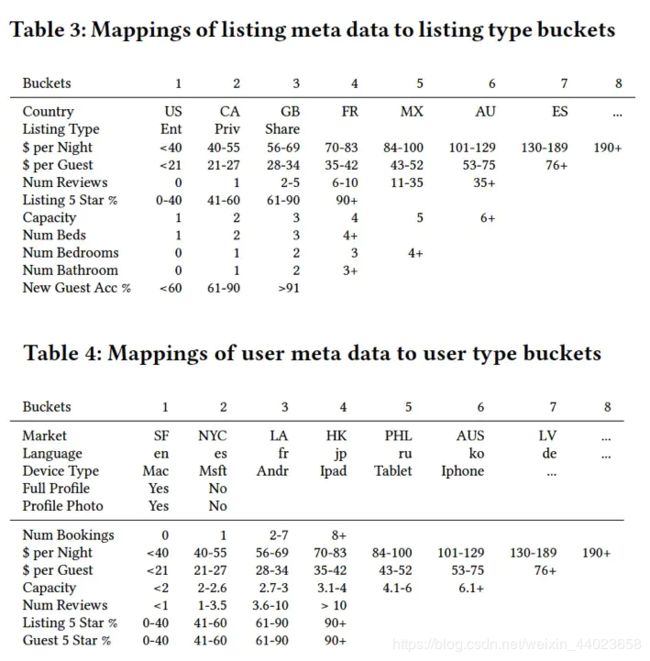最终序列由同一用户的预订序列构成（相同用户在不同时间段，user_type可能不同）：

$s_b=\left(u_{typ{e}_1}{l}_{typ{e}_1},\dots ,u_{typ{e}_M}{l}_{typ{e}_M}\right)\in {\mathcal{S}}_b$

模型

ser-type更新

$\underset{\theta }{\mathrm{argmax}}{\sum }_{\left(u_t,c\right)\in {\mathcal{D}}_{book}}\log \frac{1}{1+e^{-{\mathrm{v}}_c^{\prime }\mathrm{v}{u}_t}}+{\sum }_{\left(u_t,c\right)\in {\mathcal{D}}_{neg}}\log \frac{1}{1+e^{{\mathrm{v}}_c^{\prime }{v}_{u_t}}}$

isting_type更新

$\underset{\mathbf{\theta }}{\mathrm{argmax}}{\sum }_{\left(l_t,c\right)\in {\mathcal{D}}_{book}}\log \frac{1}{1+e^{-{\mathrm{v}}_c^{\prime }{\mathrm{v}}_{lt}}}+{\sum }_{\left(l_t,c\right)\in {\mathcal{D}}_{neg}}\log \frac{1}{1+e^{{\mathrm{v}}_c^{\prime }{\mathrm{v}}_{l_t}}}$

为了提高预订成功率，考虑房东可能会拒绝订购（可能用户信誉度不高）

${\mathrm{argmax}}_{\mathbf{\theta }}{\sum }_{\left(u_t,c\right)\in {\mathcal{D}}_{book}}\log \frac{1}{1+{\exp }^{-{\mathbf{v}}_c^{\prime }{\mathbf{v}}_{u_t}}}+{\sum }_{\left(u_t,c\right)\in {\mathcal{D}}_{neg}}\log \frac{1}{1+{\exp }^{{\mathrm{v}}_c^{\prime }{\mathbf{v}}_{u_t}}}$
$+{\sum }_{\left(u_t,l_t\right)\in {\mathcal{D}}_{\text{reject}}}\log \frac{1}{1+{\exp }_{l_t^{\prime }\mathrm{v}{u}_t}}$

${\mathrm{argmax}}_{\theta }{\sum }_{\left(l_t,c\right)\in {\mathcal{D}}_{book}}\log \frac{1}{1+{\exp }^{-v_c^{\prime }{v}_{lt}}}+{\sum }_{\left(l_t,c\right)\in {\mathcal{D}}_{neg}}\log \frac{1}{1+{\exp }^{v_c^{\prime }{v}_{lt}}}$
$+{\sum }_{\left(l_t,u_t\right)\in {\mathcal{D}}_{reject}}\log \frac{1}{1+{\exp }^{v_{u_t}^{\prime }{v}_{l_t}}}$

2.2.3 Embeddings for Search Ranking
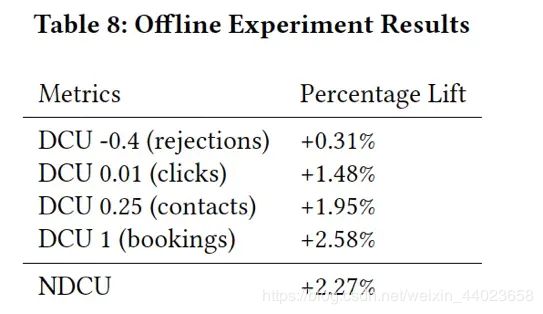
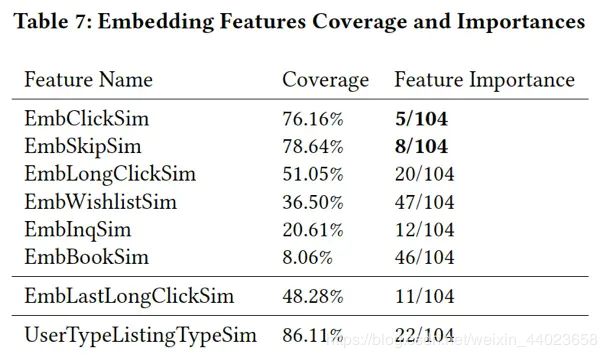
训练得到的embedding最终应用到search rank模型中。

Airbnb的搜索使用的模型是Gradient Boosting Decision Trees (GBDT)模型，模型使用了大约100个特征，如下：

embedding特征定义如下：

2.2.4 Evaluation
离线效果

embedding特征重要性

item2vec与MF的区别

首先，二者都应用了隐向量来表征实体特征，不同的是，传统的 MF 通常是 user-item 矩阵，而 Item2Vec 通过滑动窗口样本生成的方式构造出的则更像是 item-item 矩阵；另外，二者得到隐向量的方式也不同，MF 利用均方差损失，使预测得分与已有得分之间的误差尽可能地小，而 Item2Vec 则是利用空间信息并借助了最大似然估计的思想，使用对数损失，使上下文关系或者共现关系构造出的正样本的 item Pair 出现的概率可能地大；此外训练 Item2Vec 的时候还要引入负样本，这也是与 MF 不同的地方。

对于二者在推荐效果上的差异，一个经验是传统 MF 推荐会让热门内容经常性排在前面，而 Item2vec 能更好的学到中频内容的相似性。Iterm2Vec 加上较短的时间窗口，相似推荐会比 MF 好很多。

通俗点的Item2vec

把场景转换到一个新闻媒体如A公司。

在A公司的多个页面中，电商公司B有他们的一个主页，专门介绍他们公司一些产品促销，抢购和发布会什么的。

公司A目前有很多用户的浏览数据，如用户u浏览了公司A的页面a1，a2，a3等。

把这些数据处理一下，整合成word2vec能处理的数据，如下

U1  a1,a2,a3……

U2  a2,a3,a5,……

U3  a1,a3,a6,……

其中u1，u2，u3表示不同的用户，后面的一串表示这些用户的浏览记录，如U1 a1,a2,a3表示用户u1先浏览了页面a1，再浏览a2，然后浏览了a3,……

这些数据还不符合word2vec的输入数据格式，把第一列去掉，变成下面的样子

a1,a2,a3……

a2,a3,a5,……

a1,a3,a6,……

这些数据就可以作为word2vec的输入数据了。

就把这些数据作为word2vec的训练数据，词向量维度为3，进行训练，完成后得到下面的输出

A1  (0.3,-0.5,0.1)

A2  (0.1,0.4,0.2)

A3  (-0.3,0.7,0.8)

……

An  (0.7,-0.1,0.3)

就得到了每个页面的向量。

这些向量有啥意义呢？其实单个向量的意义不大，只是用这些向量可以计算一个东西——距离，这个距离是页面之间的距离，如页面a1和a2可以用欧式距离或者cos距离计算公式来计算一个距离，这个距离是有意义的，表示的是两个网页在用户浏览的过程中的相似程度（也可以认为是这两个页面的距离越近，被同一个人浏览的概率越大）。注意这个距离的绝对值本身也是没有意义的，但是这个距离的相对大小是有意义的，意思就是说，假设页面a1跟a2、a3、a4的距离分别是0.3、0.4、0.5，这0.3、0.4、0.5没啥意义，但是相对来说，页面a2与a1的相似程度就要比a3和a4要大。

那么这里就有玄机了，如果页面a1是电商公司B的主页，页面a2、a3、a4与a1的距离在所有页面里面是最小的，其他都比这三个距离要大，那么就可以认为同一个用户u浏览a1的同时，浏览a2、a3、a4的概率也比较大，那么反过来，一个用户经常浏览a2、a3、a4，那么浏览a1的概率是不是也比较大呢？从实验看来可以这么认为的。同时还可以得到一个推论，就是用户可能会喜欢a1这个页面对应的广告主的广告。

这个在实验中实际上也出现过的。这里模拟一个例子吧，如a1是匹克体育用品公司在媒体公司A上的官网，a2是湖人队比赛数据页，a3是热火队的灌水讨论区，a4是小牛队的球员讨论区。这个结果看起来是相当激动人心的。

根据这样的一个结果，就可以在广告主下单的那个页面上增加一个条件——经常浏览的相似页面推荐，功能就是——在广告主过来选条件的时候，可以选择那些经常浏览跟自己主页相似的页面的用户。举个例子就是，当匹克体育用品公司来下单的时候，页面上给它推荐了几个经常浏览页面的粉丝：湖人队比赛数据页，热火队的灌水讨论区，小牛队的球员讨论区。意思是说，目标人群中包括了经常浏览这三个页面的人。

这个功能上线后是获得过很多广告主的好评的。

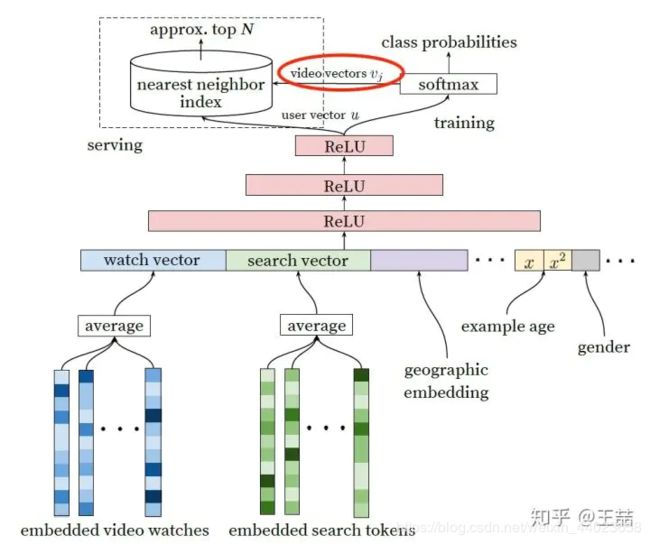
YouTube 的 user 和 video embedding 网络

参考自：
会飞的珊瑚虫
Emma
王喆的机器学习笔记