朴素贝叶斯算法--垃圾邮件过滤
文章目录
- 一、朴素贝叶斯概述
- 1、贝叶斯决策理论
- 2、条件概率
- 3、朴素贝叶斯
- 4、朴素贝叶斯一般过程
- 二、朴素贝叶斯算法--垃圾邮件
- 1、准备数据:从文本中构建词向量
- 2、训练算法:从词向量计算概率
- 3、测试算法:根据现实情况修改分类器
- 5、垃圾邮件分类
一、朴素贝叶斯概述
1、贝叶斯决策理论
假设现在我们有一个数据集,它由两类数据组成,我们现在用P1表示数据点属于类别1的概率,用P2表示数据点属于类别2的概率,那么对于一个新数据点X,可以用下面的规则来判断它的类别:
□如果P1(X)>P2(X), 那么类别为1。
□如果P1(X)
2、条件概率
条件概率就是就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
公式:P(A|B) = P(AB)/P(B)
3、朴素贝叶斯
贝叶斯准则告诉我们如何交换条件概率中的条件与结果,可以使用下面的计算方法:
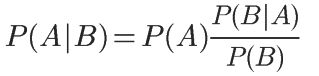
P(A)称为"先验概率",即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
朴素贝叶斯则做了条件独立性的假设,每个特征之间相互独立。
4、朴素贝叶斯一般过程
⑴收集数据:可以使用任何方法。
(2)准备数据:需要数值型或者布尔型数据。
(3)分析数据:有大量特征时,绘制特征作用不大,此时使用直方图效果更好。
(4)训练算法:计算不同的独立特征的条件概率。
(5)测试算法:计算错误率。
(6)使用算法:一个常见的朴素贝叶斯应用是文档分类。可以在任意的分类场景中使用朴素贝叶斯命类器,不一定非要是文本。
二、朴素贝叶斯算法–垃圾邮件
1、准备数据:从文本中构建词向量
把文本看成单词向量或者词条向量,也就是说将句子转换为向量。考虑出现在所有文档中的所有单词,再决定将哪些词纳人词汇表或者说所要的词汇集合,然后必须要将每一篇文档转换为词汇表上的向量。
词表到向量的转换函数:
第一个函数 loadDataSet() 创建了一些实验样本。该函数返回的第一个变量是进行词条切分后的文档集合,返回的第二个变量是一个类别标签的集合。函数createVocabList()会创建一个包含在所有文档中出现的不重复词的列表,为此使用set 数据类型。将词条列表输给set构造函数,set就会返回一个不重复词表。使用函数setOfWords2Vec(),该函数的输人参数为词汇表及某个文档,输出的是文档向量,向量的每一元素为1或0,分别表示词汇表中的单词在输人文档中是否出现。函数首先创建一个和词汇表等长的向量,并将其元素都设置为0 。接着,遍历文档中的所有词,如果出现了词汇表中的单词,则将输出的文档向量中的对应值设为1。
# 函数loadDataSet() 创建了一些实验样本。该函数返回的第一个变量是进行词条切分后的文档集合,第二个变量为自定义的类别
def loadDataSet():
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0, 1, 0, 1, 0, 1]
return postingList, classVec
# 创建不重复词库列表
def createVocabList(dataSet):
vocabSet = set([]) #创建一个空集
for document in dataSet:
vocabSet = vocabSet | set(document) #创建两个集合的并集
return list(vocabSet)
# 输出文档向量
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0]*len(vocabList) #创建一个元素都为0的向量
#遍历数据集单词
for word in inputSet:
#存在单词在词袋中则
if word in vocabList:
#index用于找到第一个与之匹配的下标
returnVec[vocabList.index(word)] = 1
else:
print ("the word: %s is not in my Vocabulary!" % word)
return returnVec
dataSet,classVec = loadDataSet()
vocabset = createVocabList(dataSet)
print(vocabset)
returnVec = setOfWords2Vec(vocabset,dataSet[0])
print(returnVec)
2、训练算法:从词向量计算概率
准备数据介绍了如何将一组单词转换为一组数字,接下来看看如何使用这些数字计算概率。
假设现在已经知道一个词是否出现在一篇文档中,也知道该文档所属的类别。接下来运用上面介绍的朴素贝叶斯公式计算概率:
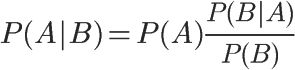
对每个类计算该值,然后比较这两个概率值的大小。
首先可以通过类别1中文档数除以总的文档数来计算概率P(A)。接下来计算P(B|A) , 这里就要用到朴素贝叶斯假设。如果将B展开为一个个独立特征,那么就可以将上述概率写作P(b1,b2,…bn|A)。这里假设所有词都互相独立,该假设也称作条件独立性假设,它意味着可以使用P(b1|A)(b2|A)(b3|A)…(bn|A)来计算上述概率,这就极大地简化了计算的过程。
from numpy import *
# 函数loadDataSet() 创建了一些实验样本。该函数返回的第一个变量是进行词条切分后的文档集合,第二个变量为自定义的类别
def loadDataSet():
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0, 1, 0, 1, 0, 1]
return postingList, classVec
# 创建不重复词库列表
def createVocabList(dataSet):
vocabSet = set([]) #创建一个空集
for document in dataSet:
vocabSet = vocabSet | set(document) #创建两个集合的并集
return list(vocabSet)
# 输出文档向量
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0]*len(vocabList) #创建一个元素都为0的向量
#遍历数据集单词
for word in inputSet:
#存在单词在词袋中则
if word in vocabList:
#index用于找到第一个与之匹配的下标
returnVec[vocabList.index(word)] = 1
else:
print ("the word: %s is not in my Vocabulary!" % word)
return returnVec
# 训练算法,求概率
"""
该函数的伪代码如下:
计算每个类别中的文档数目
对每篇训练文档:
对每个类别:
如果词条出现文档中―增加该词条的计数值
增加所有词条的计数值
对每个类别:
对每个词条:
将该词条的数目除以总词条数目得到条件概率
返回每个类别的条件概率
"""
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
# 初始化概率
p0Num = zeros(numWords); p1Num = zeros(numWords)
p0Denom = 0.0; p1Denom = 0.0
# 遍历文档,向量相加
for i in range(numTrainDocs):
if trainCategory[i] == 1: # 侮辱类文档,向量相加
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else: # 非侮辱类文档向量相加
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = p1Num/p1Denom # 各个单词在侮辱类中出现的概率
p0Vect = p0Num/p0Denom # 各个单词在非侮辱类中出现的概率
return p0Vect,p1Vect,pAbusive
dataSet, classVec = loadDataSet()
vocabset = createVocabList(dataSet)
trainMat = []
for postinDoc in dataSet:
trainMat.append(setOfWords2Vec(vocabset,postinDoc))
p0Vect, p1Vect, pAbusive = trainNB0(trainMat,classVec)
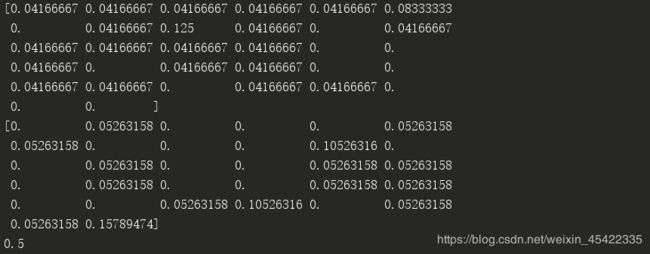
print(p0Vect) # 非侮辱类词向量概率
print(p1Vect) # 侮辱类词向量概率
print(pAbusive) #侮辱性文档的概率
3、测试算法:根据现实情况修改分类器
问题一:利用贝叶斯分类器对文档进行分类时,要计算多个概率的乘积以获得文档属于某个类别的概率,即计算P(b1|A)(b2|A)(b3|A)…(bn|A) 。如果其中一个概率值为0 ,那么最后的乘积也为0。
解决 :为降低这种影响,可以将所有词的出现数初始化为1,并将分母初始化为2。
p0Num = ones(numWords); p1Num = ones(numWords)
p0Denom = 2.0; p1Denom = 2.0
问题二:相乘值过小可能溢出。这是由于太多很小的数相乘造成的。当计算乘积P(b1|A)(b2|A)(b3|A)…(bn|A) ,由于大部分因子都非常小,所以程序会下溢出或者得到不正确的答案。
解决:在实际中对概率取对数的形式,可以防止相乘是溢出。
p1Vect = log(p1Num/p1Denom)
p0Vect = log(p0Num/p0Denom)
构建好完整的分类器后,进行测试分类。
from numpy import *
# 函数loadDataSet() 创建了一些实验样本。该函数返回的第一个变量是进行词条切分后的文档集合,第二个变量为自定义的类别
def loadDataSet():
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0, 1, 0, 1, 0, 1]
return postingList, classVec
# 创建不重复词库列表
def createVocabList(dataSet):
vocabSet = set([]) #创建一个空集
for document in dataSet:
vocabSet = vocabSet | set(document) #创建两个集合的并集
return list(vocabSet)
# 输出文档向量
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0]*len(vocabList) #创建一个元素都为0的向量
#遍历数据集单词
for word in inputSet:
#存在单词在词袋中则
if word in vocabList:
#index用于找到第一个与之匹配的下标
returnVec[vocabList.index(word)] = 1
else:
print ("the word: %s is not in my Vocabulary!" % word)
return returnVec
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = zeros(numWords); p1Num = zeros(numWords)
p0Denom = 0.0; p1Denom = 0.0
# 遍历文档,向量相加
for i in range(numTrainDocs):
if trainCategory[i] == 1: # 侮辱类文档,向量相加
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else: # 非侮辱类文档向量相加
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = p1Num/p1Denom # 各个单词在侮辱类中出现的概率
p0Vect = p0Num/p0Denom # 各个单词在非侮辱类中出现的概率
return p0Vect,p1Vect,pAbusive
# 测试算法
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
#计算abusive的概率
p1 = sum(vec2Classify * p1Vec) + log(pClass1)
#计算not abusive概率
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
#看哪个概率大
if p1 > p0:
return 1
else:
return 0
def testingNB():
# test_list=[]; test_class=[0,1]
#加载数据集
listOPosts,listClasses = loadDataSet()
#创建词汇袋
myVocabList = createVocabList(listOPosts)
trainMat=[]
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V,p1V,pAb = trainNB0(array(trainMat),array(listClasses))
testEntry = ['love', 'my', 'dalmation']
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print (testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
testEntry = ['stupid', 'garbage']
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print (testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
testingNB()
5、垃圾邮件分类
我们将每个词的出现与否作为一个特征,这可以被描述为词集模型。如果一个词在文档中出现不止一次,这可能意味着包含该词是否出现在文档中所不能表达的某种信息,这种方法被称为词袋模型化。
在词袋中,每个单词可以出现多次,而在词集中,每个词只能出现一次。为适应词袋模型,需要对函数setOfWords2Vec()稍加修改,修改后的函数称为bagOfWords2VecMN()。它与函数setOfWords2Vec()几乎
完全相同,唯一不同的是每当遇到一个单词时,它会增加词向量中的对应值,而不只是将对应的数值设为1。
数据:emai数据集
函数textParse():对文档句子进行切分、处理。
函数spamTest()对贝叶斯垃圾邮件分类器进行自动化处理。本例中共有50封电子邮件,并不是很多,其中的10封电子邮件被随机选择为测试集。进行误差测试,求出错误率。
from numpy import *
#统计列表中所有不重复的单词,词汇袋
def createVocabList(dataSet):
#定义词汇集
vocabSet = set([]) #set集合为不会有重复词的集合
#遍历数据集
for document in dataSet:
#把每个文档合并到词汇袋中
vocabSet = vocabSet | set(document) #union of the two sets
return list(vocabSet)
# 训练算法
def trainNB0(trainMatrix,trainCategory):
#计算文档的数目
numTrainDocs = len(trainMatrix)
#计算词袋单词的数目
numWords = len(trainMatrix[0])
#计算类别的概率 abusive的文档站文档总数的百分比
pAbusive = sum(trainCategory)/float(numTrainDocs)
#初始化计数器,1行*numWords列
#p0是not abusive p1是abusive
#为什么是不是0矩阵?
#因为如果是0的话,按照贝叶斯公式,p(W0|1)*p(W1|1)
#如果任意概率为0则全为0所以初始值为1
#同时下面分母初始化2
p0Num = ones(numWords); p1Num = ones(numWords)
#初始化分母
p0Denom = 2.0; p1Denom = 2.0
#遍历数据集中每个文档
for i in range(numTrainDocs):
#如果这文档是abusive类的计算它的abusive比例
if trainCategory[i] == 1:
#储存每个词在abusive下出现次数
p1Num += trainMatrix[i]
#储存abusive词的总数目
p1Denom += sum(trainMatrix[i])
else:
#储存每个词在not abusive的出现次数
p0Num += trainMatrix[i]
#储存not abusive词的总数目
p0Denom += sum(trainMatrix[i])
#使用log是为了防止数据向下溢出
# 计算abusive下每个词出现的概率
p1Vect = log(p1Num/p1Denom) #change to log()各个单词在侮辱类中出现的概率
# 计算not abusive下每个词出现的概率
p0Vect = log(p0Num/p0Denom) #change to log()各个单词在非侮辱类中出现的概率
#返回词出现的概率和文档为abusice的概率
return p0Vect,p1Vect,pAbusive
#贝叶斯分类
#第一个参数是要被训练的向量
#后面三个参数是根据上面一个函数处理训练样本后得到的参数
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
#计算abusive的概率
p1 = sum(vec2Classify * p1Vec) + log(pClass1)
#计算not abusive概率
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
#看哪个概率大
if p1 > p0:
return 1
else:
return 0
#计算文档单词在某个词袋中出现的次数
# 把单词转换成向量,用对比已经有得词袋,计算词出现的次数
def bagOfWords2VecMN(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
return returnVec
# 输入字符串,输出单词列表
def textParse(bigString):
import re
listOfTokens = re.split(r'\W+', bigString)
return [tok.lower() for tok in listOfTokens if len(tok) > 2]
def spamTest():
# 定义docList文档列表,classList类别列表,fullText所有文档词汇
docList=[]; classList = []; fullText =[]
#遍历文件夹内文件
for i in range(1,26):
# 定义并读取垃圾邮件文件的词汇分割列表
wordList = textParse(open('email/spam/%d.txt' % i).read())
# 将词汇列表加到文档列表中
docList.append(wordList)
# 将所有词汇列表汇总到fullText中
fullText.extend(wordList)
# 文档类别为1,spam
classList.append(1)
# 读取非垃圾邮件的文档
wordList = textParse(open('email/ham/%d.txt' % i).read())
# 添加到文档列表中,注意append和extend的区别,append直接加列表,extend加元素
docList.append(wordList)
# 添加到所有词汇列表中
fullText.extend(wordList)
# 类别为0,非垃圾邮件
classList.append(0)
# 创建词汇列表
vocabList = createVocabList(docList)
# 定义训练集的索引和测试集
trainingSet = list(range(50)); testSet=[]
# 随机的选择10个作为测试集
for i in range(10):
#随机索引
randIndex = int(random.uniform(0,len(trainingSet)))
#将随机选择的文档加入测试集
testSet.append(trainingSet[randIndex])
#从训练集中删除随机选择的文档
del(trainingSet[randIndex])
#定义训练集的矩阵和类别
trainMat=[]; trainClasses = [];
# test_list=[];test_class=[]
#遍历训练集,求先验概率和条件概率
for docIndex in trainingSet:
#将词汇列表变成向量放到trainList中
trainMat.append(bagOfWords2VecMN(vocabList, docList[docIndex]))
#添加训练集的类标签
trainClasses.append(classList[docIndex])
#计算先验概率,条件概率
p0V,p1V,pSpam = trainNB0(array(trainMat),array(trainClasses))
errorCount = 0
#对测试集分类
for docIndex in testSet: #classify the remaining items
#将测试集向量化
wordVector = bagOfWords2VecMN(vocabList, docList[docIndex]) #bagOfWords2VecMN函数将词汇向量化和计算次数 setOfWords2Vec将词汇向量化
# 对测试数据进行分类
if classifyNB(array(wordVector),p0V,p1V,pSpam) != classList[docIndex]:
#错误的话错误计数加一
errorCount += 1
print( "classification error",docList[docIndex])
print ('the error rate is: ',float(errorCount)/len(testSet))
return vocabList,fullText
spamTest()