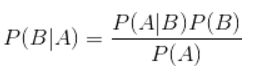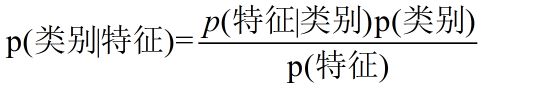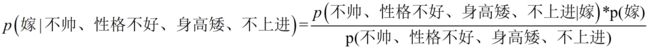机器学习十大经典算法之朴素贝叶斯分类
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。
分类问题
从数学角度来说,分类问题可做如下定义:已知集合 C = y 1 , y 2 , . . . . y n C={{y_{1},y_{2},....y_{n}} } C=y1,y2,....yn和 I = x 1 , x 2 , x 3 . . . . . . x n I=x_{1}, x_{2}, x_{3}......x_{n} I=x1,x2,x3......xn,确定映射规则y = f(),使得任意 x i ϵ I x_{i}\epsilon I xiϵI有且仅有一个$y_{i}\epsilon C , 使 得 ,使得 ,使得y_{i}\epsilon f(x_{i} ) $成立。
其中C叫做类别集合,其中每一个元素是一个类别,而I叫做项集合(特征集合),其中每一个元素是一个待分类项,f叫做分类器。分类算法的任务就是构造分类器f。
下面以一个实例来讲解:
朴素贝叶斯分类
那么既然是朴素贝叶斯分类算法,它的核心算法是下面这个贝叶斯公式:
也可以换成如下表达式:
所以我们最终求的p(类别|特征)即可!
例题分析
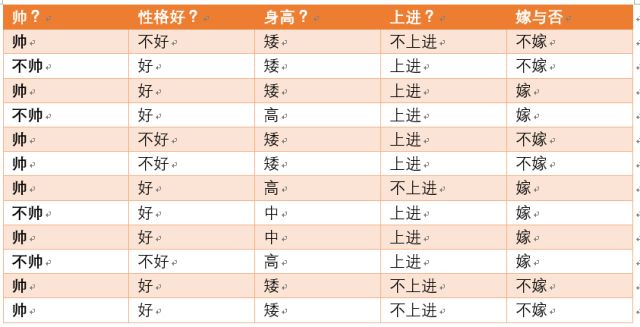
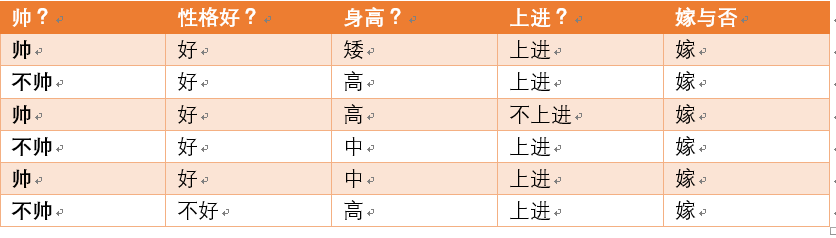
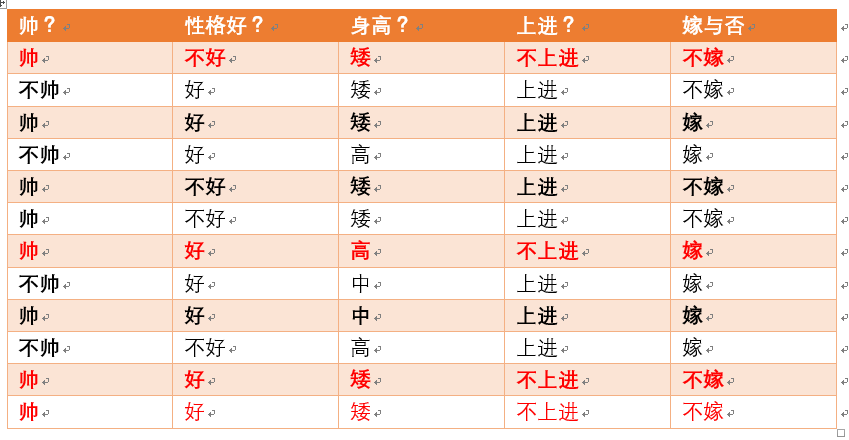
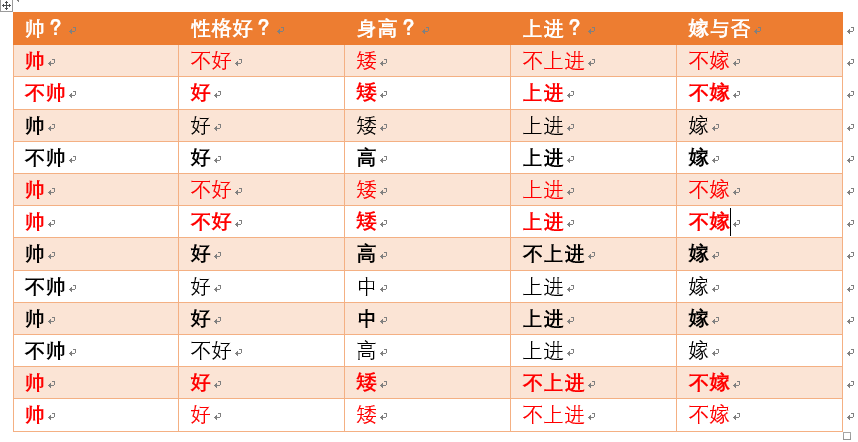
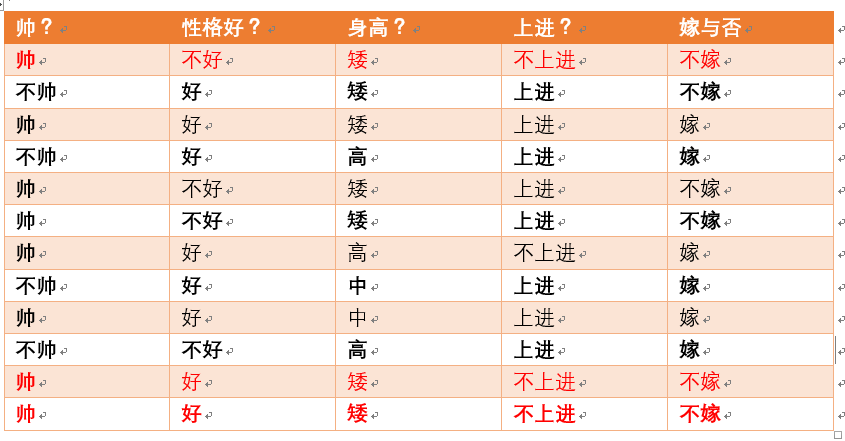
给定数据如下:
现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!
这里我们联系到朴素贝叶斯公式:
我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量,p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)(至于为什么能求,后面会讲,那么就太好了,将待求的量转化为其它可求的值,这就相当于解决了我们的问题!)
那么这三个量是如何求得?
是根据已知训练数据统计得来,下面详细给出该例子的求解过程。
回忆一下我们要求的公式如下:
那么我只要求得p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)即可,好的,下面我分别求出这几个概率,最后一比,就得到最终结果。
p(不帅、性格不好、身高矮、不上进|嫁) = p(不帅|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁),那么我就要分别统计后面几个概率,也就得到了左边的概率!
为什么这个等式成立呢?要使这个成立,需要各个特征互相独立。朴素贝叶斯分类有朴素一词的来源,就是假设各个特征之间相互独立,那么这个等式就成立了!
我们将上面公式整理一下如下:
下面我将一个一个的进行统计计算(在数据量很大的时候,根据中心极限定理,频率是等于概率的,这里只是一个例子,所以我就进行统计即可)。
p(嫁)=?
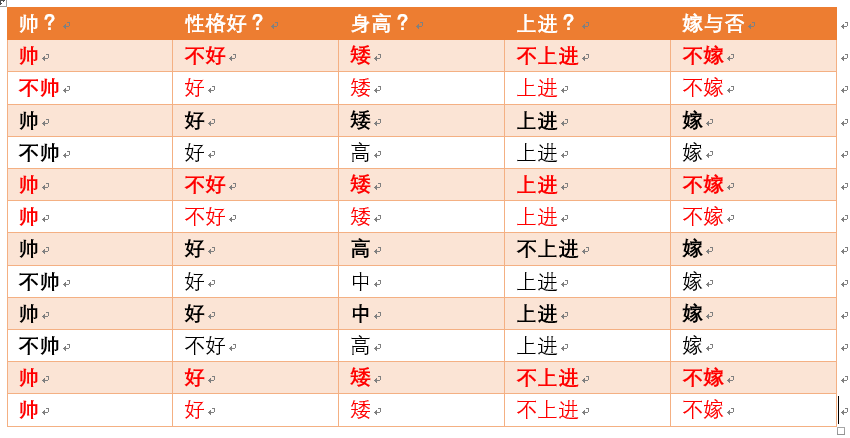
首先我们整理训练数据中,嫁的样本数如下:
则 p(嫁) = 6/12(总样本数) = 1/2
p(不帅|嫁)=?统计满足样本数如下:
则p(不帅|嫁) = 3/6 = 1/2
p(性格不好|嫁)= ?统计满足样本数如下:
则p(性格不好|嫁)= 1/6
p(矮|嫁) = ?统计满足样本数如下:
则p(矮|嫁) = 1/6
p(不上进|嫁) = ?统计满足样本数如下:
则p(不上进|嫁) = 1/6
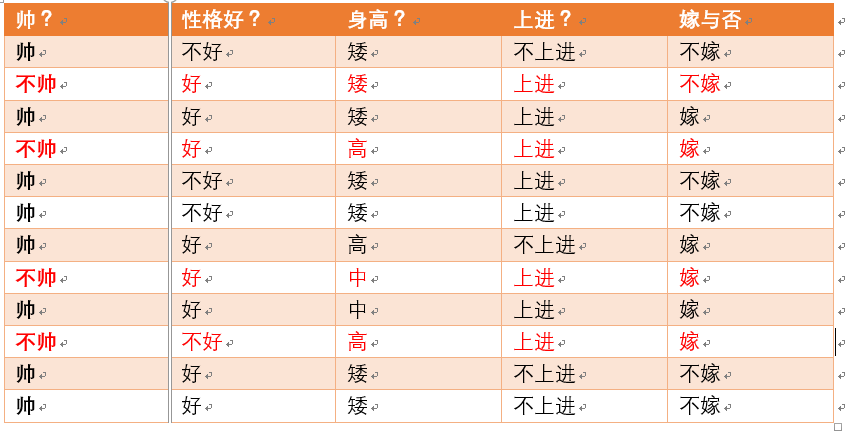
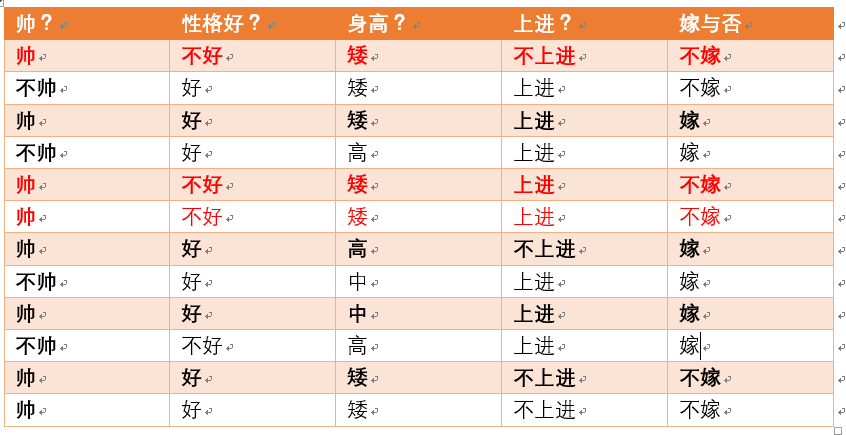
下面开始求分母,p(不帅),p(性格不好),p(矮),p(不上进)
统计样本如下:
不帅统计如上红色所示,占4个,那么p(不帅) = 4/12 = 1/3
性格不好统计如上红色所示,占4个,那么p(性格不好) = 4/12 = 1/3
身高矮统计如上红色所示,占7个,那么p(身高矮) = 7/12
不上进统计如上红色所示,占4个,那么p(不上进) = 4/12 = 1/3
到这里,要求p(不帅、性格不好、身高矮、不上进|嫁)的所需项全部求出来了,下面我带入进去即可,
= (1/2*1/6*1/6*1/6*1/2)/(1/3*1/3*7/12*1/3)
下面我们根据同样的方法来求p(不嫁|不帅,性格不好,身高矮,不上进),完全一样的做法,为了方便理解,我这里也走一遍帮助理解。首先公式如下:
下面我也一个一个来进行统计计算,这里与上面公式中,分母是一样的,于是我们分母不需要重新统计计算!
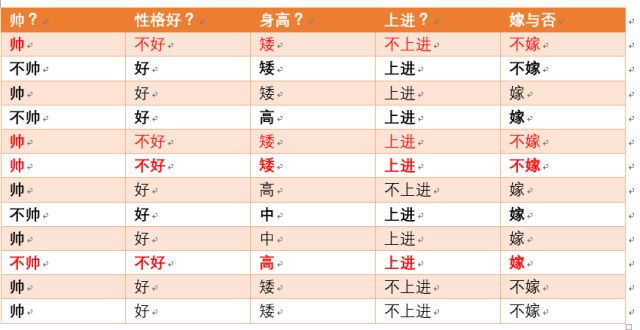
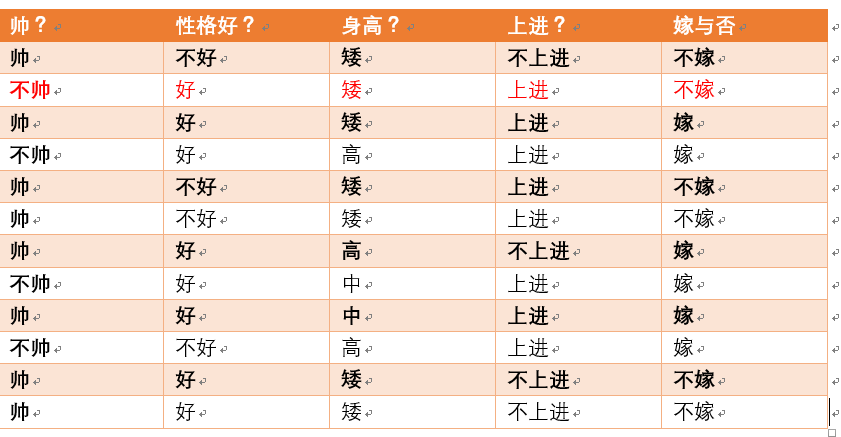
p(不嫁)=?根据统计计算如下(红色为满足条件):
则p(不嫁)=6/12 = 1/2
p(不帅|不嫁) = ?统计满足条件的样本如下(红色为满足条件):
则p(不帅|不嫁) = 1/6
p(性格不好|不嫁) = ?据统计计算如下(红色为满足条件):
则p(性格不好|不嫁) =3/6 = 1/2
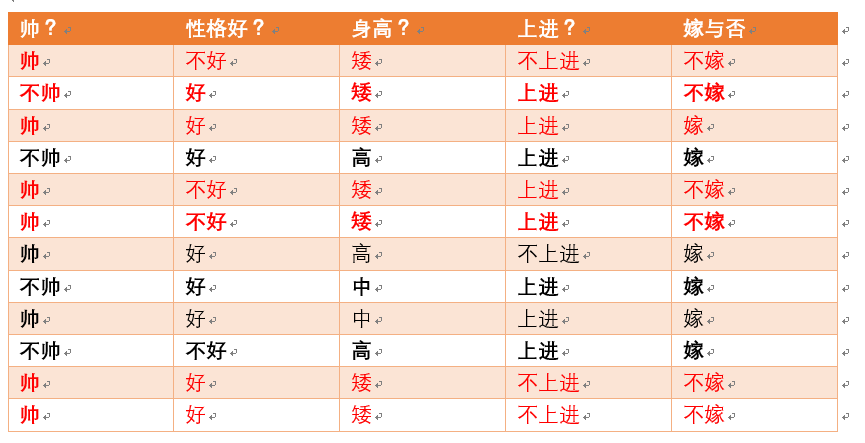
p(矮|不嫁) = ?据统计计算如下(红色为满足条件):
则p(矮|不嫁) = 6/6 = 1
p(不上进|不嫁) = ?据统计计算如下(红色为满足条件):
则p(不上进|不嫁) = 3/6 = 1/2
那么根据公式:
p (不嫁|不帅、性格不好、身高矮、不上进) = ((1/6*1/2*1*1/2)*1/2)/(1/3*1/3*7/12*1/3)
很显然(1/6*1/2*1*1/2) > (1/2*1/6*1/6*1/6*1/2)
于是有p (不嫁|不帅、性格不好、身高矮、不上进)>p (嫁|不帅、性格不好、身高矮、不上进)
所以我们根据朴素贝叶斯算法可以给这个女生答案,是不嫁!!!!
算法流程
实际应用方式:
- 若任务对预测速度要求较高,则对给定的训练集,可将朴素贝叶斯分类器涉及的所有概率估值事先计算好存储起来,这样在进行预测时只需要 “查表” 即可进行判别;
- 若任务数据更替频繁,则可采用 “懒惰学习” (lazy learning) 方式,先不进行任何训练,待收到预测请求时再根据当前数据集进行概率估值;
- 若数据不断增加,则可在现有估值的基础上,仅对新增样本的属性值所涉及的概率估值进行计数修正即可实现增量学习。
朴素贝叶斯分类算法实现
https://github.com/Asia-Lee/Naive_Bayes
参考文献
李航博士《统计学习方法》
知乎专栏:https://zhuanlan.zhihu.com/p/26262151