排列组合算法的代码实现——附Python源码

一、问题描述

假设我们从数组[1,2,3,4,5,6]中，取出三个不重复的数，求所有可能的组合，数据不多，我们手动列举一下：

二、枚举法

看着几个三角形，是不是觉得很有规律，让人立刻想到是递归，但是递归式很容易让人混乱的算法，最简单的实现方法无疑是暴力枚举法，先写为敬，代码如下：

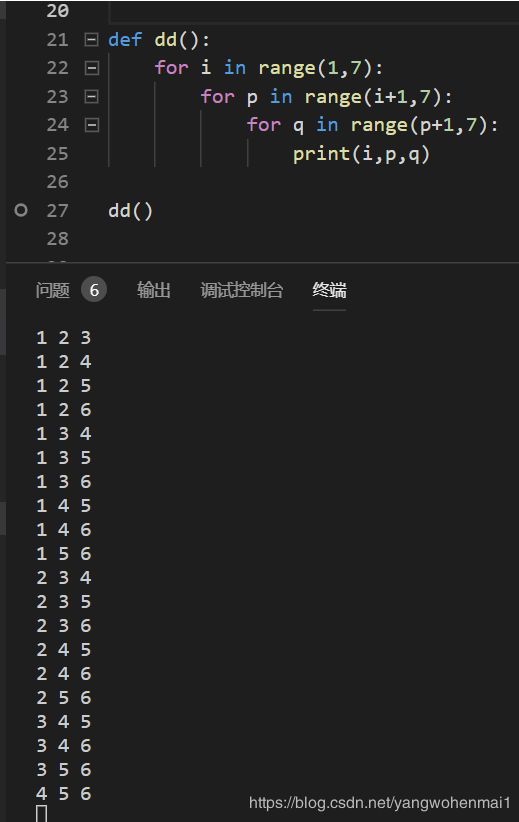
def dd():
    for i in range(1,7):
        for p in range(i+1,7):
            for q in range(p+1,7):
                print(i,p,q)

dd()

这里的range(1,7)可以理解为一个数组的索引，实现了这个数组索引的所有组合，数组中的元素的所有组合也自然就列出来了，运行结果如下：

三、递归法

当然，无法否认暴力破解永远是最low的方法，递归看起来就高大上很多。

递归的思想其实也很清晰，如果是从m个数据中取n个数，我们就要构建那个游标，按顺序取数，每一次移动最后一个游标，最后一个游标移动到数组末尾后，开始移动上一级游标，这样依次调整就完成了递归。

比如长度为6的数组中取3个数，我们就要假设有3个游标，i1，i2，i3。i1指向1，i2指向2，i3指向3。算法开始时，我们首先移动最后一个游标i3：

i3初始指向3，输出1，2，3

i3移动到4，输出1，2，4

i3移动到5，输出1，2，5

i3移动到6，输出1，2，6

此时i3已经移动到数组末尾，我们开始调整上一级游标，此时i1指向1，i2指向3，i3指向4。算法开始时，我们首先移动最后一个游标i3：

i3初始指向4，输出：1，3，4

i3移动到5，输出：1，3，5

i3移动到6，输出：1，3，6

此时i3已经移动到数组末尾，我们开始调整上一级游标，此时i1指向1，i2指向4，i3指向5。算法开始时，我们首先移动最后一个游标i3：

i3初始指向5，输出：1，3，4

i3移动到6，输出：1，3，6

…………

…………

通过上述算法不断的移动游标，就是实现了递归算法，下面看两种递归的写法：

data = [1, 2, 3, 4, 5, 6]
def combine(data, l):
    result = []
    tmp = [0]*l
    length = len(data)
    def next_num(li=0, ni=0):
        if ni == l:
            result.append(copy.copy(tmp))
            return
        for lj in range(li,length):
            tmp[ni] = data[lj]
            next_num(lj+1, ni+1)
    next_num()
    print(result)
    return result


combine(data,3)

#target每组要输出的元素个数，step游标
def combine(data, step, select_data, target_num):
    #如果已经凑齐一组完成的组合，输出当前组
    if len(select_data) == target_num:
        print(select_data)
        return
    #如果游标超过数组长，说明后续元素都被遍历完成，跳转到上一个元素的循环
    if step >= len(data):
        return
    #把选中的元素加入临时输出列表中，n个一组作为输出
    select_data.append(data[step])
    #递归调整最后一位
    combine(data, step + 1, select_data, target_num)
    #构建一个新组合，首先要删掉上次输出组中药排除的元素
    select_data.pop()
    #递归向上调整一位元素                         
    combine(data, step + 1, select_data, target_num)

if __name__ == '__main__':
    data = [1, 2, 3, 4, 5, 6]
    combine(data, 0, [], 3)

 

 参考资料：

https://blog.csdn.net/zhaoshuaiwjm/article/details/78189003

https://blog.csdn.net/Deeven123/article/details/82970560