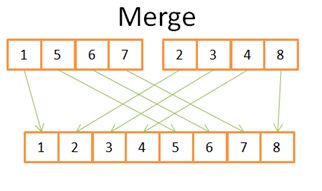
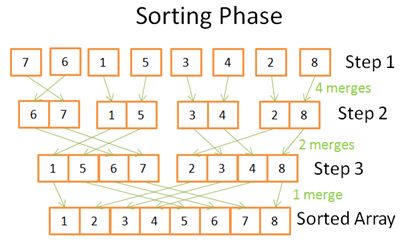
- Google earth studio 简介
陟彼高冈yu
旅游
GoogleEarthStudio是一个基于Web的动画工具,专为创作使用GoogleEarth数据的动画和视频而设计。它利用了GoogleEarth强大的三维地图和卫星影像数据库,使用户能够轻松地创建逼真的地球动画、航拍视频和动态地图可视化。网址为https://www.google.com/earth/studio/。GoogleEarthStudio是一个基于Web的动画工具,专为创作使用G
- 关于提高复杂业务逻辑代码可读性的思考
编程经验分享
开发经验java数据库开发语言
目录前言需求场景常规写法拆分方法领域对象总结前言实际工作中大部分时间都是在写业务逻辑,一般都是三层架构,表示层(Controller)接收客户端请求,并对入参做检验,业务逻辑层(Service)负责处理业务逻辑,一般开发都是在这一层中写具体的业务逻辑。数据访问层(Dao)是直接和数据库交互的,用于查数据给业务逻辑层,或者是将业务逻辑层处理后的数据写入数据库。简单的增删改查接口不用多说,基本上写好一
- SQL Server_查询某一数据库中的所有表的内容
qq_42772833
SQLServer数据库sqlserver
1.查看所有表的表名要列出CrabFarmDB数据库中的所有表(名),可以使用以下SQL语句:USECrabFarmDB;--切换到目标数据库GOSELECTTABLE_NAMEFROMINFORMATION_SCHEMA.TABLESWHERETABLE_TYPE='BASETABLE';对这段SQL脚本的解释:SELECTTABLE_NAME:这个语句的作用是从查询结果中选择TABLE_NAM
- 深入理解 MultiQueryRetriever:提升向量数据库检索效果的强大工具
nseejrukjhad
数据库python
深入理解MultiQueryRetriever:提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域,高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用,但仍存在一些局限性。本文将介绍一种创新的解决方案:MultiQueryRetriever,它通过自动生成多个查询视角来增强检索效果,提高结果的相关性和多样性。MultiQueryRetriever的工
- MongoDB Oplog 窗口
喝醉酒的小白
MongoDB运维
在MongoDB中,oplog(操作日志)是一个特殊的日志系统,用于记录对数据库的所有写操作。oplog允许副本集成员(通常是从节点)应用主节点上已经执行的操作,从而保持数据的一致性。它是MongoDB副本集实现数据复制的基础。MongoDBOplog窗口oplog窗口是指在MongoDB副本集中,从节点可以用来同步数据的时间范围。这个窗口通常由以下因素决定:Oplog大小:oplog的大小是有限
- python os 环境变量
CV矿工
python开发语言numpy
环境变量:环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里,比如数据库密码,个人账户密码,如果写进自己本机的环境变量里,程序用的时候通过os.environ.get()取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量:os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
- 【PG】常见数据库、表属性设置
江无羡
数据库
PG的常见属性配置方法数据库复制、备份相关表的复制标识单表操作批量表操作链接数据库复制、备份相关表的复制标识单表操作通过ALTER语句单独更改一张表的复制标识。ALTERTABLE[tablename]REPLICAIDENTITYFULL;批量表操作通过代码块的方式,对某个schema中的所有表一起更新其复制标识。SELECTtablename,CASErelreplidentWHEN'd'TH
- nosql数据库技术与应用知识点
皆过客,揽星河
NoSQLnosql数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
- insert into select 主键自增_mybatis拦截器实现主键自动生成
weixin_39521651
insertintoselect主键自增mybatisdelete返回值mybatisinsert返回主键mybatisinsert返回对象mybatisplusinsert返回主键mybatisplus插入生成id
前言前阵子和朋友聊天,他说他们项目有个需求,要实现主键自动生成,不想每次新增的时候,都手动设置主键。于是我就问他,那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成,因此为了项目稳定性,不会切换id的生成方式。朋友问我有没有什么实现思路,他们公司的orm框架是mybatis,我就建议他说,不然让你老大把mybatis切换成mybatis-plus。mybat
- 关于Mysql 中 Row size too large (> 8126) 错误的解决和理解
秋刀prince
mysqlmysql数据库
提示:啰嗦一嘴,数据库的任何操作和验证前,一定要记得先备份!!!不会有错;文章目录问题发现一、问题导致的可能原因1、页大小2、行格式2.1compact格式2.2Redundant格式2.3Dynamic格式2.4Compressed格式3、BLOB和TEXT列二、解决办法1、修改页大小(不推荐)2、修改行格式3、修改数据类型为BLOB和TEXT列4、其他优化方式(可以参考使用)4.1合理设置数据
- Java爬虫框架(一)--架构设计
狼图腾-狼之传说
java框架java任务html解析器存储电子商务
一、架构图那里搜网络爬虫框架主要针对电子商务网站进行数据爬取,分析,存储,索引。爬虫:爬虫负责爬取,解析,处理电子商务网站的网页的内容数据库:存储商品信息索引:商品的全文搜索索引Task队列:需要爬取的网页列表Visited表:已经爬取过的网页列表爬虫监控平台:web平台可以启动,停止爬虫,管理爬虫,task队列,visited表。二、爬虫1.流程1)Scheduler启动爬虫器,TaskMast
- MongoDB知识概括
GeorgeLin98
持久层mongodb
MongoDB知识概括MongoDB相关概念单机部署基本常用命令索引-IndexSpirngDataMongoDB集成副本集分片集群安全认证MongoDB相关概念业务应用场景:传统的关系型数据库(如MySQL),在数据操作的“三高”需求以及应对Web2.0的网站需求面前,显得力不从心。解释:“三高”需求:①Highperformance-对数据库高并发读写的需求。②HugeStorage-对海量数
- Mongodb Error: queryTxt ETIMEOUT xxxx.wwwdz.mongodb.net
佛一脚
errorreactmongodb数据库
背景每天都能遇到奇怪的问题,做个记录,以便有缘人能得到帮助!换了一台电脑开发nextjs程序。需要连接mongodb数据,对数据进行增删改查。上一台电脑好好的程序,新电脑死活连不上mongodb数据库。同一套代码,没任何修改,搞得我怀疑人生了,打开浏览器进入mongodb官网毫无问题,也能进入线上系统查看数据,网络应该是没问题。于是我尝试了一下手机热点,这次代码能正常跑起来,连接数据库了!!!是不
- 入门MySQL——查询语法练习
K_un
前言:前面几篇文章为大家介绍了DML以及DDL语句的使用方法,本篇文章将主要讲述常用的查询语法。其实MySQL官网给出了多个示例数据库供大家实用查询,下面我们以最常用的员工示例数据库为准,详细介绍各自常用的查询语法。1.员工示例数据库导入官方文档员工示例数据库介绍及下载链接:https://dev.mysql.com/doc/employee/en/employees-installation.h
- 博客网站制作教程
2401_85194651
javamaven
首先就是技术框架:后端:Java+SpringBoot数据库:MySQL前端:Vue.js数据库连接:JPA(JavaPersistenceAPI)1.项目结构blog-app/├──backend/│├──src/main/java/com/example/blogapp/││├──BlogApplication.java││├──config/│││└──DatabaseConfig.java
- ubuntu安装wordpress
lissettecarlr
1安装nginx网上安装方式很多,这就就直接用apt-get了apt-getinstallnginx不用启动啥,然后直接在浏览器里面输入IP:80就能看到nginx的主页了。如果修改了一些配置可以使用下列命令重启一下systemctlrestartnginx.service2安装mysql输入安装前也可以更新一下软件源,在安装过程中将会让你输入数据库的密码。sudoapt-getinstallmy
- 深入浅出 -- 系统架构之负载均衡Nginx的性能优化
xiaoli8748_软件开发
系统架构系统架构负载均衡nginx
一、Nginx性能优化到这里文章的篇幅较长了,最后再来聊一下关于Nginx的性能优化,主要就简单说说收益最高的几个优化项,在这块就不再展开叙述了,毕竟影响性能都有多方面原因导致的,比如网络、服务器硬件、操作系统、后端服务、程序自身、数据库服务等,对于性能调优比较感兴趣的可以参考之前《JVM性能调优》中的调优思想。优化一:打开长连接配置通常Nginx作为代理服务,负责分发客户端的请求,那么建议开启H
- 【RabbitMQ 项目】服务端:数据管理模块之绑定管理
月夜星辉雪
rabbitmq分布式
文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字:交换机的路由交换算法中会用到没有是否持久化的标志,因为绑定是否持久化取决于交换机和队列是否持久化,只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子,两端连接着交换机和队列,当一方不存在,它就没有存在的必要了定义绑定持久化类构造函数:如果数据库文件不存在则创建,打开数据库,创建binding_table插入
- 计算机毕业设计PHP仓储综合管理系统(源码+程序+VUE+lw+部署)
java毕设程序源码王哥
php课程设计vue.js
该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程。欢迎交流项目运行环境配置:phpStudy+Vscode+Mysql5.7+HBuilderX+Navicat11+Vue+Express。项目技术:原生PHP++Vue等等组成,B/S模式+Vscode管理+前后端分离等等。环境需要1.运行环境:最好是小皮phpstudy最新版,我们在这个版本上开发的。其他版本理论上也可以。2.开发
- 3.增删改查--连接查询
问女何所忆
关系型数据库的一个特点就是,多张表之间存在关系,以致于我们可以连接多张表进行查询操作,所以连接查询会是关系型数据库中最常见的操作。连接查询主要分为三种,交叉连接、内连接和外连接,我们一个个说。1、交叉连接交叉连接其实连接查询的第一个阶段,它简单表现为两张表的笛卡尔积形式,具体例子:如果你没学过数学中的笛卡尔积概念,你可以这样简单的理解这里的交叉连接:两张表的交叉连接就是一个连接合并的过程,T1表中
- docker from指令的含义_多个FROM-含义
weixin_39722188
dockerfrom指令的含义
小编典典什么是基本图片?一组文件,加上EXPOSE端口ENTRYPOINT和CMD。您可以添加文件并基于该基础图像构建新图像,Dockerfile并以FROM指令开头:后面提到的图像FROM是新图像的“基础图像”。这是否意味着如果我neo4j/neo4j在FROM指令中声明,则在运行映像时,neo数据库将自动运行并且可在端口7474的容器中使用?仅当您不覆盖CMD和时ENTRYPOINT。但是图像
- Redis:缓存击穿
我的程序快快跑啊
缓存redisjava
缓存击穿(热点key):部分key(被高并发访问且缓存重建业务复杂的)失效,无数请求会直接到数据库,造成巨大压力1.互斥锁:可以保证强一致性线程一:未命中之后,获取互斥锁,再查询数据库重建缓存,写入缓存,释放锁线程二:查询未命中,未获得锁(已由线程一获得),等待一会,缓存命中互斥锁实现方式:redis中setnxkeyvalue:改变对应key的value,仅当value不存在时执行,以此来实现互
- mysql学习教程,从入门到精通,TOP 和MySQL LIMIT 子句(15)
知识分享小能手
大数据数据库MySQLmysql学习oracle数据库开发语言adb大数据
1、TOP和MySQLLIMIT子句内容在SQL中,不同的数据库系统对于限制查询结果的数量有不同的实现方式。TOP关键字主要用于SQLServer和Access数据库中,而LIMIT子句则主要用于MySQL、PostgreSQL(通过LIMIT/OFFSET语法)、SQLite等数据库中。下面将分别详细介绍这两个功能的语法、语句以及案例。1.1、TOP子句(SQLServer和Access)1.1
- ERROR 1064 (42000): You have an error in your SQL syntax; check the manual that corresponds to your
†徐先森®
Oracle数据库Web相关错误集
createtablestudents(idintunsignedprimarykeyauto_increment,namevarchar(50)notnull,ageintunsigned,highdecimal(3,2),genderenum('男','女','中性','保密','妖')default'保密',cls_idintunsigned);在对数据库插入如上带有中文带有默认值的字段的时
- Redis 有哪些危险命令?如何防范?
花小疯
redis缓存数据库危险命令大数据
Redis有哪些危险命令?Redis的危险命令主要有以下几个:1.keys客户端可查询出所有存在的键。2.flushdb删除Redis中当前所在数据库中的所有记录,并且此命令从不会执行失败。3.flushall删除Redis中所有数据库中的所有记录,不止是当前所在数据库,并且此命令从不会执行失败。4.config客户端可修改Redis配置。怎么禁用和重命名危险命令?看下redis.conf默认配置
- 【Golang】 Golang 的 GORM 库中的 Rows 函数
不爱洗脚的小滕
golang开发语言后端
文章目录前言一、Rows函数解释二、代码实现三、总结前言在使用Go语言进行数据库操作时,GORM(GoObject-RelationalMapping)库是一个常用的工具。它提供了一种简洁和强大的方式来处理数据库操作。本文将介绍GORM库中的Rows函数,这是一个用于执行原生SQL查询并返回结果的函数。一、Rows函数解释在GORM库中,Rows函数用于执行原生SQL查询并返回*sql.Rows结
- 接口测试如何设计测试用例
李蕴Ronnie
接口测试用例设计方式针对每个必填参数,都设计一条参数为空的测试用例必填参数不存在传的参数值在数据库中不存在添加数据接口,传入已有的数据重复添加编辑数据接口,各个字段分别编辑,合并编辑参数数据类型限制,针对每个参数设计一条参数值类型不符合的逆向用例参数自身取值范围,针对所有参数,设计一条每个参数值在取值范围内最大值的正向测试用例是否满足前提条件(token、headers),几个前提条件几条用例针对
- Hadoop架构
henan程序媛
hadoop大数据分布式
一、案列分析1.1案例概述现在已经进入了大数据(BigData)时代,数以万计用户的互联网服务时时刻刻都在产生大量的交互,要处理的数据量实在是太大了,以传统的数据库技术等其他手段根本无法应对数据处理的实时性、有效性的需求。HDFS顺应时代出现,在解决大数据存储和计算方面有很多的优势。1.2案列前置知识点1.什么是大数据大数据是指无法在一定时间范围内用常规软件工具进行捕捉、管理和处理的大量数据集合,
- 非关系型数据库
天秤-white
nosql
一、为什么要用Nosql1.单机MySQL的时代。一个基本的网站访问量一般不会太大,单个数据库完全足够。那时候更多使用的静态网页html,服务器根本没有太大压力。这时候网站的瓶颈是什么?-数据量如果太大,一个机器放不下。-数据量太大需要建立数据的索引(B+Tree),一个服务器内存放不下。-访问量读写混合,一个服务器承受不了。2.memcached缓存+MySQL+垂直拆分(读写分离)。网站80%
- 六、全局锁和表锁:给表加个字段怎么有这么多阻碍
nieniemin
数据库锁设计的初衷是处理并发问题。作为多用户共享的资源,当出现并发访问的时候,数据库需要合理地控制资源的访问规则。而锁就是用来实现这些访问规则的重要数据结构。根据加锁的范围,MySQL里面的锁大致可以分成全局锁、表级锁和行锁三类。6.1全局锁全局锁就是对整个数据库实例加锁。MySQL提供了一个加全局读锁的方法,命令是Flushtableswithreadlock(FTWRL)。当你需要让整个库处于
- 枚举的构造函数中抛出异常会怎样
bylijinnan
javaenum单例
首先从使用enum实现单例说起。
为什么要用enum来实现单例?
这篇文章(
http://javarevisited.blogspot.sg/2012/07/why-enum-singleton-are-better-in-java.html)阐述了三个理由:
1.enum单例简单、容易,只需几行代码:
public enum Singleton {
INSTANCE;
- CMake 教程
aigo
C++
转自:http://xiang.lf.blog.163.com/blog/static/127733322201481114456136/
CMake是一个跨平台的程序构建工具,比如起自己编写Makefile方便很多。
介绍:http://baike.baidu.com/view/1126160.htm
本文件不介绍CMake的基本语法,下面是篇不错的入门教程:
http:
- cvc-complex-type.2.3: Element 'beans' cannot have character
Cb123456
springWebgis
cvc-complex-type.2.3: Element 'beans' cannot have character
Line 33 in XML document from ServletContext resource [/WEB-INF/backend-servlet.xml] is i
- jquery实例:随页面滚动条滚动而自动加载内容
120153216
jquery
<script language="javascript">
$(function (){
var i = 4;$(window).bind("scroll", function (event){
//滚动条到网页头部的 高度,兼容ie,ff,chrome
var top = document.documentElement.s
- 将数据库中的数据转换成dbs文件
何必如此
sqldbs
旗正规则引擎通过数据库配置器(DataBuilder)来管理数据库,无论是Oracle,还是其他主流的数据都支持,操作方式是一样的。旗正规则引擎的数据库配置器是用于编辑数据库结构信息以及管理数据库表数据,并且可以执行SQL 语句,主要功能如下。
1)数据库生成表结构信息:
主要生成数据库配置文件(.conf文
- 在IBATIS中配置SQL语句的IN方式
357029540
ibatis
在使用IBATIS进行SQL语句配置查询时,我们一定会遇到通过IN查询的地方,在使用IN查询时我们可以有两种方式进行配置参数:String和List。具体使用方式如下:
1.String:定义一个String的参数userIds,把这个参数传入IBATIS的sql配置文件,sql语句就可以这样写:
<select id="getForms" param
- Spring3 MVC 笔记(一)
7454103
springmvcbeanRESTJSF
自从 MVC 这个概念提出来之后 struts1.X struts2.X jsf 。。。。。
这个view 层的技术一个接一个! 都用过!不敢说哪个绝对的强悍!
要看业务,和整体的设计!
最近公司要求开发个新系统!
- Timer与Spring Quartz 定时执行程序
darkranger
springbean工作quartz
有时候需要定时触发某一项任务。其实在jdk1.3,java sdk就通过java.util.Timer提供相应的功能。一个简单的例子说明如何使用,很简单: 1、第一步,我们需要建立一项任务,我们的任务需要继承java.util.TimerTask package com.test; import java.text.SimpleDateFormat; import java.util.Date;
- 大端小端转换,le32_to_cpu 和cpu_to_le32
aijuans
C语言相关
大端小端转换,le32_to_cpu 和cpu_to_le32 字节序
http://oss.org.cn/kernel-book/ldd3/ch11s04.html
小心不要假设字节序. PC 存储多字节值是低字节为先(小端为先, 因此是小端), 一些高级的平台以另一种方式(大端)
- Nginx负载均衡配置实例详解
avords
[导读] 负载均衡是我们大流量网站要做的一个东西,下面我来给大家介绍在Nginx服务器上进行负载均衡配置方法,希望对有需要的同学有所帮助哦。负载均衡先来简单了解一下什么是负载均衡,单从字面上的意思来理解就可以解 负载均衡是我们大流量网站要做的一个东西,下面我来给大家介绍在Nginx服务器上进行负载均衡配置方法,希望对有需要的同学有所帮助哦。
负载均衡
先来简单了解一下什么是负载均衡
- 乱说的
houxinyou
框架敏捷开发软件测试
从很久以前,大家就研究框架,开发方法,软件工程,好多!反正我是搞不明白!
这两天看好多人研究敏捷模型,瀑布模型!也没太搞明白.
不过感觉和程序开发语言差不多,
瀑布就是顺序,敏捷就是循环.
瀑布就是需求、分析、设计、编码、测试一步一步走下来。而敏捷就是按摸块或者说迭代做个循环,第个循环中也一样是需求、分析、设计、编码、测试一步一步走下来。
也可以把软件开发理
- 欣赏的价值——一个小故事
bijian1013
有效辅导欣赏欣赏的价值
第一次参加家长会,幼儿园的老师说:"您的儿子有多动症,在板凳上连三分钟都坐不了,你最好带他去医院看一看。" 回家的路上,儿子问她老师都说了些什么,她鼻子一酸,差点流下泪来。因为全班30位小朋友,惟有他表现最差;惟有对他,老师表现出不屑,然而她还在告诉她的儿子:"老师表扬你了,说宝宝原来在板凳上坐不了一分钟,现在能坐三分钟。其他妈妈都非常羡慕妈妈,因为全班只有宝宝
- 包冲突问题的解决方法
bingyingao
eclipsemavenexclusions包冲突
包冲突是开发过程中很常见的问题:
其表现有:
1.明明在eclipse中能够索引到某个类,运行时却报出找不到类。
2.明明在eclipse中能够索引到某个类的方法,运行时却报出找不到方法。
3.类及方法都有,以正确编译成了.class文件,在本机跑的好好的,发到测试或者正式环境就
抛如下异常:
java.lang.NoClassDefFoundError: Could not in
- 【Spark七十五】Spark Streaming整合Flume-NG三之接入log4j
bit1129
Stream
先来一段废话:
实际工作中,业务系统的日志基本上是使用Log4j写入到日志文件中的,问题的关键之处在于业务日志的格式混乱,这给对日志文件中的日志进行统计分析带来了极大的困难,或者说,基本上无法进行分析,每个人写日志的习惯不同,导致日志行的格式五花八门,最后只能通过grep来查找特定的关键词缩小范围,但是在集群环境下,每个机器去grep一遍,分析一遍,这个效率如何可想之二,大好光阴都浪费在这上面了
- sudoku solver in Haskell
bookjovi
sudokuhaskell
这几天没太多的事做,想着用函数式语言来写点实用的程序,像fib和prime之类的就不想提了(就一行代码的事),写什么程序呢?在网上闲逛时发现sudoku游戏,sudoku十几年前就知道了,学生生涯时也想过用C/Java来实现个智能求解,但到最后往往没写成,主要是用C/Java写的话会很麻烦。
现在写程序,本人总是有一种思维惯性,总是想把程序写的更紧凑,更精致,代码行数最少,所以现
- java apache ftpClient
bro_feng
java
最近使用apache的ftpclient插件实现ftp下载,遇见几个问题,做如下总结。
1. 上传阻塞,一连串的上传,其中一个就阻塞了,或是用storeFile上传时返回false。查了点资料,说是FTP有主动模式和被动模式。将传出模式修改为被动模式ftp.enterLocalPassiveMode();然后就好了。
看了网上相关介绍,对主动模式和被动模式区别还是比较的模糊,不太了解被动模
- 读《研磨设计模式》-代码笔记-工厂方法模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
package design.pattern;
/*
* 工厂方法模式:使一个类的实例化延迟到子类
* 某次,我在工作不知不觉中就用到了工厂方法模式(称为模板方法模式更恰当。2012-10-29):
* 有很多不同的产品,它
- 面试记录语
chenyu19891124
招聘
或许真的在一个平台上成长成什么样,都必须靠自己去努力。有了好的平台让自己展示,就该好好努力。今天是自己单独一次去面试别人,感觉有点小紧张,说话有点打结。在面试完后写面试情况表,下笔真的好难,尤其是要对面试人的情况说明真的好难。
今天面试的是自己同事的同事,现在的这个同事要离职了,介绍了我现在这位同事以前的同事来面试。今天这位求职者面试的是配置管理,期初看了简历觉得应该很适合做配置管理,但是今天面
- Fire Workflow 1.0正式版终于发布了
comsci
工作workflowGoogle
Fire Workflow 是国内另外一款开源工作流,作者是著名的非也同志,哈哈....
官方网站是 http://www.fireflow.org
经过大家努力,Fire Workflow 1.0正式版终于发布了
正式版主要变化:
1、增加IWorkItem.jumpToEx(...)方法,取消了当前环节和目标环节必须在同一条执行线的限制,使得自由流更加自由
2、增加IT
- Python向脚本传参
daizj
python脚本传参
如果想对python脚本传参数,python中对应的argc, argv(c语言的命令行参数)是什么呢?
需要模块:sys
参数个数:len(sys.argv)
脚本名: sys.argv[0]
参数1: sys.argv[1]
参数2: sys.argv[
- 管理用户分组的命令gpasswd
dongwei_6688
passwd
NAME: gpasswd - administer the /etc/group file
SYNOPSIS:
gpasswd group
gpasswd -a user group
gpasswd -d user group
gpasswd -R group
gpasswd -r group
gpasswd [-A user,...] [-M user,...] g
- 郝斌老师数据结构课程笔记
dcj3sjt126com
数据结构与算法
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
- yii2 cgridview加上选择框进行操作
dcj3sjt126com
GridView
页面代码
<?=Html::beginForm(['controller/bulk'],'post');?>
<?=Html::dropDownList('action','',[''=>'Mark selected as: ','c'=>'Confirmed','nc'=>'No Confirmed'],['class'=>'dropdown',])
- linux mysql
fypop
linux
enquiry mysql version in centos linux
yum list installed | grep mysql
yum -y remove mysql-libs.x86_64
enquiry mysql version in yum repositoryyum list | grep mysql oryum -y list mysql*
install mysq
- Scramble String
hcx2013
String
Given a string s1, we may represent it as a binary tree by partitioning it to two non-empty substrings recursively.
Below is one possible representation of s1 = "great":
- 跟我学Shiro目录贴
jinnianshilongnian
跟我学shiro
历经三个月左右时间,《跟我学Shiro》系列教程已经完结,暂时没有需要补充的内容,因此生成PDF版供大家下载。最近项目比较紧,没有时间解答一些疑问,暂时无法回复一些问题,很抱歉,不过可以加群(334194438/348194195)一起讨论问题。
----广告-----------------------------------------------------
- nginx日志切割并使用flume-ng收集日志
liyonghui160com
nginx的日志文件没有rotate功能。如果你不处理,日志文件将变得越来越大,还好我们可以写一个nginx日志切割脚本来自动切割日志文件。第一步就是重命名日志文件,不用担心重命名后nginx找不到日志文件而丢失日志。在你未重新打开原名字的日志文件前,nginx还是会向你重命名的文件写日志,linux是靠文件描述符而不是文件名定位文件。第二步向nginx主
- Oracle死锁解决方法
pda158
oracle
select p.spid,c.object_name,b.session_id,b.oracle_username,b.os_user_name from v$process p,v$session a, v$locked_object b,all_objects c where p.addr=a.paddr and a.process=b.process and c.object_id=b.
- java之List排序
shiguanghui
list排序
在Java Collection Framework中定义的List实现有Vector,ArrayList和LinkedList。这些集合提供了对对象组的索引访问。他们提供了元素的添加与删除支持。然而,它们并没有内置的元素排序支持。 你能够使用java.util.Collections类中的sort()方法对List元素进行排序。你既可以给方法传递
- servlet单例多线程
utopialxw
单例多线程servlet
转自http://www.cnblogs.com/yjhrem/articles/3160864.html
和 http://blog.chinaunix.net/uid-7374279-id-3687149.html
Servlet 单例多线程
Servlet如何处理多个请求访问?Servlet容器默认是采用单实例多线程的方式处理多个请求的:1.当web服务器启动的