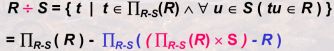数据库：关系代数

关系代数概述

关系代数运算的特点：

基于集合，提供了一系列的关系代数操作：并、差、笛卡尔积、选择、投影和更名等基本操作

以及交、连接和关系除等扩展操作，是一种集合思维的操作语言。

关系代数操作以一个或多个关系为输入，结果是有一个新的关系。

用对关系的运算来表达刚查询，需要指明所用操作，具有一定过程性。

是一种抽象的语言，是学习其他数据库语言，如SQL等的基础。

关系代数运算的基本操作

集合操作和纯关系操作：

关系代数运算的约束

并相容性

参与运算的两个关系及其相关属性之间有一定的对应性、可比性或意义关联性

定义：关系R与关系S存在相容性，当且仅当：

1  关系R和关系S的属性数目必须相同；

2 对于任意i，关系R的第i个属性的域必须和关系S的第i个属性的域相同

    假设:R(A2,A2,...,An),S(B1,B2,...,Bm)

    R和S满足并相容性：n=m并且Domain(Ai)=Domain(Bi)

示例：

    STUDENT(SID char(10), Sname char(8), Age char(3))
    PROFESSOR(PID char(10), Pname char(8), Age char(3))
    关系STUDENT 与关系PROFESSOR 是相容的，因为：
    (1)  关系R 和关系S 的属性数目都是3
    (2)  关系R 的属性SID 与关系S 的属性PID 的域都是char(10)
    (3)  关系R 的属性Sname 与关系S 的属性Sname 的域都是char(8)

    (4)  关系R 的属性Age 与关系S 的属性Age 的域都是char(3)

关系代数之基本操作

并(Uion)

定义：假设关系R和关系S并相容的，则关系R与关系S的并运算结果也是一个关系，记作：R∪S, 它由或者出现在关系R中，或者出现在S中的元组构成。

数学描述 ： R∪S ={ t | t∈R V t∈S }  中 ，其中t是元组。

并运算是将两个关系的元组合并成一个关系，在合并时去掉重复的元组。

R∪S和 S∪R运算的结果是同一个关系。

差(Difference)

定义：假设关系R和关系S是并相容的，则关系R与关系S的差运算结果也是一个关系，记作：R-S，它是由出现在关系R中但不出现在关系S中的元组构成。

数学描述： R-S ={ t | t∈RΛ t∉S }  中 ，其中t是元组。

R-S与S-R是不同的。

广义笛卡尔积(Cartesion Product)

 定义：关系R ()  与关系S()  的广义笛卡尔积( 简称广义积, 或 积 或笛卡尔积)  运算结果也是一个关系，记作： R x S, 它由关系R 中的元组与关系S 的元组进行所有可能的拼接( 或串接) 构成。

数学描述 ： R x S ={ | ∈R ^ ∈S }

选择(Select)

定义 ：给定一个关系R,  同时给定一个选择的条件condition( 简记con), 选择运算结果也是一个关系，记作选择运算结果也是一个关系，记作σcon (R) ,  它从关系R 中选择出满足给定条件condition 的元组构成。

数学描述 ：σcon (R)={t | t∈RΛcon(t) = ‘ 真’} ，

设R(A 1 ,A 2  , … ,A n ), t 是R 的元组, t 的分量记为的分量记为t[A i ],  或简写为A i

条件con 由逻辑运算符连接比较表达式组成

逻辑运算符：and , or, not

比较表达式：XθY, 其中X, Y是t的分量、常量或简单函数, θ是比较运算符,  θ∈{ > , ≥ , ＜ , ≤, ＝ ,  ≠}

投影(Project)

定义：给定一个关系R，投影运算结果也是一个关系，记作ΠA(R)，它从关系R中选出属性包含在A中的列构成。

设R{A1,A2,...,An}

{Ai1,Ai2,...,Aik}∈{A1,A2,...,An}

t[Ai]表示元组t中相应属性的分量

投影运算可以对原关系的列在投影后重新排列

投影操作从给定关系中选出某些列组成新的关系，而选择操作是从给定关系中选出某些行组成新的关系

关系代数之扩展操作

交(Intersection)

  定义：假设关系R 和关系S 是并相容的，则关系R 与关系S的交运算结果也是一个关系，记作：R ∩S,  它由同时出现在系关系R和关系S 中的元组构成。

数学描述 ： R∩S ={ t | t∈RΛt∈S } 中 ，其中t 是元组。

R∩S 和 和 S ∩R  运算的结果是同一个关系

交运算可以通过差运算来实现：R∩S = R - (R - S) = S- (S - R)

“θ-连接”操作

  定义系 ：给定关系R 和关系S, R 与S 的θ连接运算结果也是一个关系，记作 ，它由关系它由关系R 和关系S 

的笛卡尔积中,  选取R 中属性A与S中属性B 之间满足θ条件的元组构成。

数学描述 ：

设R(A1,A2,… ,An), A∈{A1,A2,… ,An}S(B1,B2,… ,Bm), B∈{B1,B2,…,Bm}

t是关系R 中的元组，s是关系S中的元组属性A和属性B具有可比性

在实际应用中，θ- 连接操作经常与投影、选择操作一起使用

关系代数之复杂扩展操作

“除”操作

前提条件：给定关系R(A1,A2,...,An)为n度关系，关系S(B1,B2,...,Bm)为m度关系。如果可以进行关系R与关系S的除运算，当且仅当：属性集{B1,B2,...,Bm}是属性集{A1,A2,...,An}的真子集，即m

定义：关系R和关系S除运算结果也是一个关系，记作R÷S分两部分来定义。

1 属性：

设属性集{C1,C2,...,Ck,}={A1,A2,...,An}-{B1,B2,...,Bm}，则有k=n-m，则R÷S结果关系是一k度(n-m度)关系，由{C1,C2,...,Ck}属性构成。

2 元组：

再设关系R()和关系S()，那么R÷S结果关系为元组的集合，且满足下述条件：

元组与S中每一个元组组合形成一个新元组都是R中的某一个元组。

数学描述：

“外连接”操作

定义：两个关系R与S进行连接是，如果关系R（或S）中的元组在S（或R）中找不到相匹配的元组，则为了避免该元组信息丢失，从而将该元组与S（或R）中假定存在的全为空值的元组形成连接，放置在结果关系中，这种连接称为外连接(Outer Join)。

 外连接 =  自然连接 ( 或θ连接) +  失配的元组( 与全空元组形成的连接)

外连接的形式：左外连接、右外连接、全外连接

左外连接 =  自然连接( 或θ连接) +  左侧表中失配的元组

右外连接 =  自然连接( 或θ连接) +  右侧表中失配的元组

全外连接 =  自然连接( 或θ连接) +  两侧表中失配的元组