2021秋招-算法-BFS-DFS
LeetCode刷题总结-DFS、BFS和回溯法篇
一、深度优先搜索
一、字符匹配问题
[1.lc-301. 删除无效的括号-困难]
二、数组或字符串问题
[1. lc-329. 矩阵中的最长递增路径-困难]
[2. lc-488. 祖玛游戏-困难]
[3. lc-491. 递增子序列-中等]
三、特定场景应用问题
[1. lc-679. 24 点游戏-困难]
[2. lc-1254. 统计封闭岛屿的数目-中等]
二、广度优先搜索
一、数组或字符串问题
[1. lc-127. 单词接龙-中等]
[2. lc-1091. 二进制矩阵中的最短路径-中等]
二、特定场景应用问题
[1. lc-773. 滑动谜题-困难]
[2. lc-815. 公交路线-困难]
三、回溯法
数组或字符串问题
[1. 题号:47. 全排列 II-中等]
[2. 题号:51. N皇后-困难]
[3. 题号:131. 分割回文串-中等]
BFS-DFS总结
知乎-搜索思想—DFS & BFS(基础基础篇) 提供两种搜索思想伪代码、框架 (⭐⭐⭐)
知乎-LeetCode|一文帮你搞定BFS、DFS算法(python版)⭐⭐⭐
同样总结了模板以及常见的问题类型;
BFS-大佬写的框架,后面也是搬运此文章 ⭐⭐⭐⭐
BFS 的核心思想应该不难理解的,就是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,我们写 BFS 算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列。
BFS 相对 DFS 的最主要的区别是:BFS 找到的路径一定是最短的,但代价就是空间复杂度比 DFS 大很多,至于为什么,我们后面介绍了框架就很容易看出来了。
本文就由浅入深写两道 BFS 的典型题目,分别是「二叉树的最小高度」和「打开密码锁的最少步数」,手把手教你怎么写 BFS 算法。
一、BFS-算法框架
要说框架的话,我们先举例一下 BFS 出现的常见场景好吧,问题的本质就是让你在一幅「图」中找到从起点start到终点target的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿。
把枯燥的本质搞清楚了,再去欣赏各种问题的包装才能胸有成竹嘛。
这个广义的描述可以有各种变体,比如走迷宫,有的格子是围墙不能走,从起点到终点的最短距离是多少?如果这个迷宫带「传送门」可以瞬间传送呢?
再比如说两个单词,要求你通过某些替换,把其中一个变成另一个,每次只能替换一个字符,最少要替换几次?
再比如说连连看游戏,两个方块消除的条件不仅仅是图案相同,还得保证两个方块之间的最短连线不能多于两个拐点。你玩连连看,点击两个坐标,游戏是如何判断它俩的最短连线有几个拐点的?
再比如……
净整些花里胡哨的,这些问题都没啥奇技淫巧,本质上就是一幅「图」,让你从一个起点,走到终点,问最短路径。这就是 BFS 的本质,框架搞清楚了直接默写就好。

记住下面这个框架就 OK 了:
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj())
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
/* 划重点:更新步数在这里 */
step++;
}
}
# python
def BFS(start, target):
queue = [] # 核心数据结构
visited = set() # 避免走回头路
queue.append(start) # 将起点加入队列
visited.add(start)
step = 0 # 记录扩散的步数
while queue:
queue_size = len(queue) # 当前step 队列中的元素
# 将当前队列中所有节点向四周扩散
for i in range(queue_size):
curNode = queue.pop(0) # 获取当前节点
# 划重点:这里判断是否到达终点
if curNode is target:
return step
# 将curNode 的相邻节点加入队列
for (Node -x in curNode.adj()):
if (x not in visited):
queue.append(x)
visited.add(x) # 不存在pop(), 故可以保留历史信息
# 划重点: 更新步数在这里
step += 1
队列q就不说了,BFS 的核心数据结构;cur.adj()泛指cur相邻的节点,比如说二维数组中,cur上下左右四面的位置就是相邻节点;visited的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要visited。
二、二叉树的最小高度:leetcode-111-简单
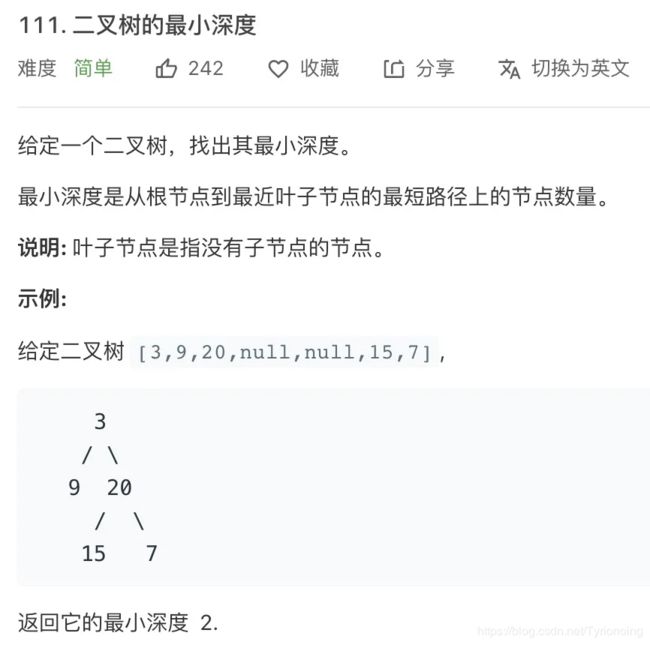
怎么套到 BFS 的框架里呢?首先明确一下起点start和终点target是什么,怎么判断到达了终点?
显然起点就是root根节点,终点就是最靠近根节点的那个「叶子节点」嘛,叶子节点就是两个子节点都是null的节点:
if not curNode.left and not curNode.right:
# 达到叶子节点
那么,按照我们上述的框架稍加改造来写解法即可:
int minDepth(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// root 本身就是一层,depth 初始化为 1
int depth = 1;
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
/* 判断是否到达终点 */
if (cur.left == null && cur.right == null)
return depth;
/* 将 cur 的相邻节点加入队列 */
if (cur.left != null)
q.offer(cur.left);
if (cur.right != null)
q.offer(cur.right);
}
/* 这里增加步数 */
depth++;
}
return depth;
}
python提交代码
# python -
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def minDepth(self, root: TreeNode) -> int:
# BFS: 时间复杂度相对DFS较低, 但是空间复杂度O(N) > DFS:O(log N)
if not root:
return 0
queue = [root] # BFS使用队列
depth = 1 # 初始化高度/深度
while queue:
# 记录队列中元素数量: 二叉树每一层node数量
queue_size = len(queue)
# 遍历二叉树一层node, 并将周围节点加入 队列
for i in range(queue_size):
# 取最先进入队列元素
curNode = queue.pop(0)
# 判断是否到达终点
if not curNode.left and not curNode.right:
return depth
# 将当前节点周围node加入队列
if curNode.left:
queue.append(curNode.left)
if curNode.right:
queue.append(curNode.right)
# 遍历一层, 深度 +1
depth += 1
二叉树是很简单的数据结构,我想上述代码你应该可以理解的吧,其实其他复杂问题都是这个框架的变形,在探讨复杂问题之前,我们解答两个问题:
1、为什么 BFS 可以找到最短距离,DFS 不行吗?
首先,你看 BFS 的逻辑,depth每增加一次,队列中的所有节点都向前迈一步,这保证了第一次到达终点的时候,走的步数是最少的。
DFS 不能找最短路径吗?其实也是可以的,但是时间复杂度相对高很多。
你想啊,DFS 实际上是靠递归的堆栈记录走过的路径,你要找到最短路径,肯定得把二叉树中所有树杈都探索完才能对比出最短的路径有多长对不对?
而 BFS 借助队列做到一次一步「齐头并进」,是可以在不遍历完整棵树的条件下找到最短距离的。
形象点说,DFS 是线,BFS 是面;DFS 是单打独斗,BFS 是集体行动。这个应该比较容易理解吧。
2、既然 BFS 那么好,为啥 DFS 还要存在?
BFS 可以找到最短距离,但是空间复杂度高,而 DFS 的空间复杂度较低。
还是拿刚才我们处理二叉树问题的例子,假设给你的这个二叉树是满二叉树,节点总数为N,对于 DFS 算法来说,空间复杂度无非就是递归堆栈,最坏情况下顶多就是树的高度,也就是O(logN)。
但是你想想 BFS 算法,队列中每次都会储存着二叉树一层的节点,这样的话最坏情况下空间复杂度应该是树的最底层节点的数量,也就是N/2,用 Big O 表示的话也就是O(N)。
由此观之,BFS 还是有代价的,一般来说在找最短路径的时候使用 BFS,其他时候还是 DFS 使用得多一些**(主要是递归代码好写)**。
好了,现在你对 BFS 了解得足够多了,下面来一道难一点的题目,深化一下框架的理解吧。
三、解开密码锁的最少次数:leetcode-752-中等

题目中描述的就是我们生活中常见的那种密码锁,若果没有任何约束,最少的拨动次数很好算,就像我们平时开密码锁那样直奔密码拨就行了。
但现在的难点就在于,不能出现deadends,应该如何计算出最少的转动次数呢?
第一步,我们不管所有的限制条件,不管deadends和target的限制,就思考一个问题:如果让你设计一个算法,穷举所有可能的密码组合,你怎么做?
穷举呗,再简单一点,如果你只转一下锁,有几种可能?总共有 4 个位置,每个位置可以向上转,也可以向下转,也就是有 8 种可能对吧。
比如说从"0000"开始,转一次,可以穷举出"1000", “9000”, “0100”, “0900”…共 8 种密码。然后,再以这 8 种密码作为基础,对每个密码再转一下,穷举出所有可能…
仔细想想,这就可以抽象成一幅图,每个节点有 8 个相邻的节点,又让你求最短距离,这不就是典型的 BFS 嘛,框架就可以派上用场了,先写出一个「简陋」的 BFS 框架代码再说别的:
// 将s[j] 向上拨动一次
String plusOne(String s, int j){
char [] ch = s.toCharArray();
if (ch[j == '9')
ch[j] = '0';
else
ch[j] += 1;
return new String(ch)
}
// 将s[i] 向下拨动一次
// BFS框架, 打印所有可能的密码
void BFS(String target){
# 初始化队列
Queue q = new LinkedList<>();
q.offer('0000')
while (!q.isEmpty()){
int sz = q.size();
// 将当前队列中的所有节点向周围扩散
for (int i = 0; i < sz; i++){
String cur = q.poll();
// 判断是否到达终点
System.out.println(cur)
// 将一个节点的相邻节点加入队列
for (int j = 0; j < 4; j++){
String up = plusOne(cur, j);
String down = minusOne(cur, j);
q.offer(up);
q.offer(down);
}
}
// 增加步数
。。。
}
return ;
}
# python版本
# s[j]向上拨动一次
def plusOne(s, j): # s: [] j:位置j
if s[j] == 9:
s[j] = 0
else:
s[j] += 1
return s
# s[i] 向下拨动一次
def minusOne(s, j):
if s[j] == 0:
s[j] = 9
else:
s[j] -= 1
return s
# BFS框架
def BFS(start, target):
queue = [[0, 0 , 0, 0]]
while queue:
queue_size = len(queue)
# 将当前节点向周围扩散
for i in range(queue_size):
curNode = queue.pop(0)
# 判断当前是否到达终点:第一次到达就返回, 就是最短路径?
if curNode == target:
return steps
# 将一个节点的相邻节点加入队列: 4位依次遍历
for j in range(4):
up = plusOne(curNode, j)
down = minusOne(curNode, j)
queue.appen(up)
queue.append(down)
steps += 1
return steps
PS:这段代码当然有很多问题,但是我们做算法题肯定不是一蹴而就的,而是从简陋到完美的。不要完美主义,咱要慢慢来,好不。
这段 BFS 代码已经能够穷举所有可能的密码组合,但显然不能完成题目,有如下问题需要解决:
1、会走回头路。比如说我们从"0000"拨到"1000",但是等从队列拿出"1000"时,还会拨出一个"0000",这样的话会产生死循环。
2、没有终止条件,按照题目要求,我们找到target就应该结束并返回拨动的次数。
3、没有对deadends的处理,按道理这些「死亡密码」是不能出现的,也就是说你遇到这些密码的时候需要跳过。
如果你能够看懂上面那段代码,真得给你鼓掌,只要按照 BFS 框架在对应的位置稍作修改即可修复这些问题:
class Solution {
// 将 s[j] 向上拨动一次
String plusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '9')
ch[j] = '0';
else
ch[j] += 1;
return new String(ch);
}
// 将 s[i] 向下拨动一次
String minusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '0')
ch[j] = '9';
else
ch[j] -= 1;
return new String(ch);
}
public int openLock(String[] deadends, String target) {
// 记录需要跳过的死亡密码
Set<String> deads = new HashSet<>();
for (String s : deadends) deads.add(s);
// 记录已经穷举过的密码,防止走回头路
Set<String> visited = new HashSet<>();
Queue<String> q = new LinkedList<>();
// 从起点开始启动广度优先搜索
int step = 0;
q.offer("0000");
visited.add("0000");
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向周围扩散 */
for (int i = 0; i < sz; i++) {
String cur = q.poll();
/* 判断是否到达终点 */
if (deads.contains(cur))
continue;
if (cur.equals(target))
return step;
/* 将一个节点的未遍历相邻节点加入队列 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up)) {
q.offer(up);
visited.add(up);
}
String down = minusOne(cur, j);
if (!visited.contains(down)) {
q.offer(down);
visited.add(down);
}
}
}
/* 在这里增加步数 */
step++;
}
// 如果穷举完都没找到目标密码,那就是找不到了
return -1;
}
}
python代码
class Solution:
def openLock(self, deadends: List[str], target: str) -> int:
# block[j] 向上拨动一次
def plusOne(block, j):
block = [int(s) for s in block]
if block[j] == 9:
block[j] = 0
else:
block[j] += 1
return ''.join([str(b) for b in block])
# block[j] 向下拨动一次
def minusOne(block, j):
block = [int(s) for s in block]
if block[j] == 0:
block[j] = 9
else:
block[j] -= 1
return ''.join([str(b) for b in block])
# 死亡密码记录
deads = set(deadends)
# 记录已经访问过的密码,路径 , 防止走回头路
# 后面添加记得 list-->
visited = set(['0000'])
# 使用队列,记录当前步数下的密码
queue = ['0000']
# 从起点开始 BFS
step = 0
while queue:
queue_size = len(queue)
# 将当前队列中的节点向周围扩散
for i in range(queue_size):
curNode = queue.pop(0)
print('-----curNode-----:', curNode)
# 判断是否到达终点
if curNode in deads:
continue
if curNode == target:
return step
# 将一个节点的未遍历相邻节点加入队列, 8个相邻
for j in range(4):
up = plusOne(curNode, j)
# 限制不走回头路
if up not in visited:
visited.add(up)
queue.append(up)
print('up_add:', up)
down = minusOne(curNode, j)
if down not in visited:
visited.add(down)
queue.append(down)
print('down_add:', down)
# 步数增加
step += 1
# 遍历完毕,未找到合适路径
return -1
至此,我们就解决这道题目了。有一个比较小的优化:可以不需要dead这个哈希集合,可以直接将这些元素初始化到visited集合中,效果是一样的,可能更加优雅一些。
四、双向 BFS 优化
你以为到这里 BFS 算法就结束了?恰恰相反。BFS 算法还有一种稍微高级一点的优化思路:双向 BFS,可以进一步提高算法的效率。
篇幅所限,这里就提一下区别:传统的 BFS 框架就是从起点开始向四周扩散,遇到终点时停止;而双向 BFS 则是从起点和终点同时开始扩散,当两边有交集的时候停止。
为什么这样能够能够提升效率呢?其实从 Big O 表示法分析算法复杂度的话,它俩的最坏复杂度都是O(N),但是实际上双向 BFS 确实会快一些,我给你画两张图看一眼就明白了:
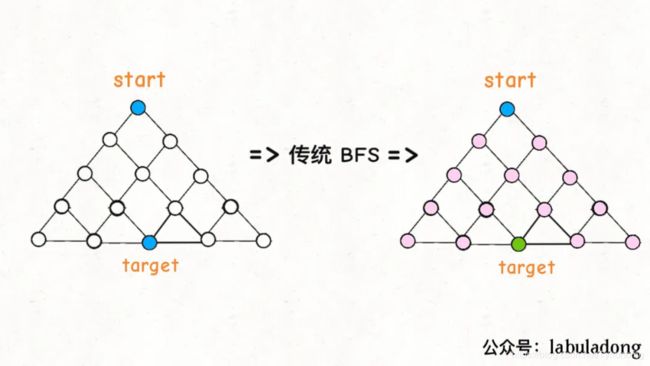
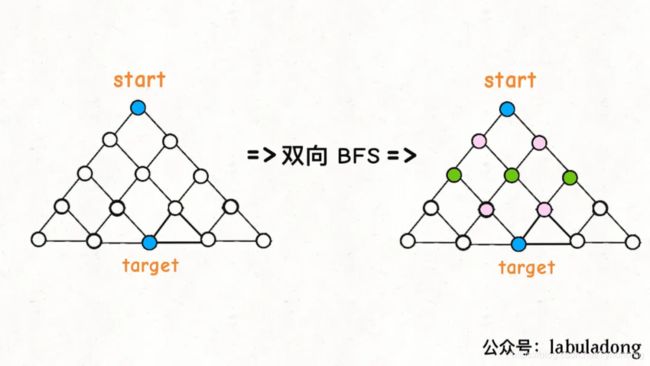
图示中的树形结构,如果终点在最底部,按照传统 BFS 算法的策略,会把整棵树的节点都搜索一遍,最后找到target;而双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离。从这个例子可以直观地感受到,双向 BFS 是要比传统 BFS 高效的。
不过,双向 BFS 也有局限,因为你必须知道终点在哪里。比如我们刚才讨论的二叉树最小高度的问题,你一开始根本就不知道终点在哪里,也就无法使用双向 BFS;但是第二个密码锁的问题,是可以使用双向 BFS 算法来提高效率的,代码稍加修改即可:
int openLock(String[] deadends, String target) {
Set deads = new HashSet<>();
for (String s : deadends) deads.add(s);
// 用集合不用队列,可以快速判断元素是否存在
Set q1 = new HashSet<>();
Set q2 = new HashSet<>();
Set visited = new HashSet<>();
int step = 0;
q1.add("0000");
q2.add(target);
while (!q1.isEmpty() && !q2.isEmpty()) {
// 哈希集合在遍历的过程中不能修改,用 temp 存储扩散结果
Set temp = new HashSet<>();
/* 将 q1 中的所有节点向周围扩散 */
for (String cur : q1) {
/* 判断是否到达终点 */
if (deads.contains(cur))
continue;
if (q2.contains(cur))
return step;
visited.add(cur);
/* 将一个节点的未遍历相邻节点加入集合 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up))
temp.add(up);
String down = minusOne(cur, j);
if (!visited.contains(down))
temp.add(down);
}
}
/* 在这里增加步数 */
step++;
// temp 相当于 q1
// 这里交换 q1 q2,下一轮 while 就是扩散 q2
q1 = q2;
q2 = temp;
}
return -1;
}
双向 BFS 还是遵循 BFS 算法框架的,只是不再使用队列,而是使用 HashSet 方便快速判断两个集合是否有交集。
另外的一个技巧点就是 while 循环的最后交换q1和q2的内容,所以只要默认扩散q1就相当于轮流扩散q1和q2。
其实双向 BFS 还有一个优化,就是在 while 循环开始时做一个判断:
// ...
while (!q1.isEmpty() && !q2.isEmpty()) {
if (q1.size() > q2.size()) {
// 交换 q1 和 q2
temp = q1;
q1 = q2;
q2 = temp;
}
// ...
为什么这是一个优化呢?
因为按照 BFS 的逻辑,队列(集合)中的元素越多,扩散之后新的队列(集合)中的元素就越多;在双向 BFS 算法中,如果我们每次都选择一个较小的集合进行扩散,那么占用的空间增长速度就会慢一些,效率就会高一些。
不过话说回来,无论传统 BFS 还是双向 BFS,无论做不做优化,从 Big O 衡量标准来看,空间复杂度都是一样的,只能说双向 BFS 是一种 trick 吧,掌握不掌握其实都无所谓。最关键的是把 BFS 通用框架记下来,反正所有 BFS 算法都可以用它套出解法。
BFS-相关题目
后期做题都尽量使用此模板进行套用
一些说明记录:
1. 列表的pop(0)方法复杂度时O(N),不能用来做队列。可以用collections.deque或queue.Queue
1.1 from collections import deque # 导入 deque包
1.2 queue = deque() # 实例化、初始化一个 队列 queue = []
1.3 queue.append((i, j)) # 队列中添加元素
1.4 queue.popleft() # queue.pop(0)
# python
def BFS(start, target):
queue = [] # 核心数据结构
visited = set() # 避免走回头路
queue.append(start) # 将起点加入队列
visited.add(start)
step = 0 # 记录扩散的步数
while queue:
# queue_size: 本质作用, 记录一步或者一层 队列中有几个元素; 如果结果不结算层、不计算多少步, 其实也没必要的;
queue_size = len(queue) # 当前step 队列中的元素
# 将当前队列中所有节点向四周扩散
for i in range(queue_size):
curNode = queue.pop(0) # 获取当前节点
# 划重点:这里判断是否到达终点
if curNode is target:
return step
# 将curNode 的相邻节点加入队列
for (Node -x in curNode.adj()):
if (x not in visited):
queue.append(x)
visited.add(x) # 不存在pop(), 故可以保留历史信息
# 划重点: 更新步数在这里
step += 1
1. leetcode-111-二叉树的最小高度-简单
2. leetcode-752-解开密码锁的最小次数-中等
3.leetcode-102. 二叉树的层序遍历-中等
102. 二叉树的层序遍历
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
# 套框架: 终止条件发生变化 ,不再是选择最短路径
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
# 思路: 使用队列,BFS
res = []
if not root:
return res
queue = [root]
while queue:
line_res = [] # 存储当前层的节点
queue_size = len(queue)
# 将当前队列节点向四周扩散
for i in range(queue_size):
curNode = queue.pop(0)
# 划重点: 判断是否到达终点
# if curNode: 不必判断: curNode.left 和 curNode.right 都已经满足了, curNode必然满足;
line_res.append(curNode.val)
# 将相邻节点加入
if curNode.left:
queue.append(curNode.left)
if curNode.right:
queue.append(curNode.right)
# 将一层节点加入result
res.append(line_res)
return res
4. leetcode-107. 二叉树的层次遍历 II-简单
107. 二叉树的层次遍历 II
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其自底向上的层次遍历为:
[
[15,7],
[9,20],
[3]
]
# 层次遍历结果反转
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
# 思路: 使用队列,BFS
res = []
if not root:
return res
queue = [root]
while queue:
line_res = [] # 存储当前层的节点
queue_size = len(queue)
# 将当前队列节点向四周扩散
for i in range(queue_size):
curNode = queue.pop(0)
# 划重点: 判断是否到达终点
# if curNode: 不必判断: curNode.left 和 curNode.right 都已经满足了, curNode必然满足;
line_res.append(curNode.val)
# 将相邻节点加入
if curNode.left:
queue.append(curNode.left)
if curNode.right:
queue.append(curNode.right)
# 将一层节点加入result
res.append(line_res)
return res[::-1]
5.leetcode-103. 二叉树的锯齿形层次遍历-中等
103. 二叉树的锯齿形层次遍历
给定一个二叉树,返回其节点值的锯齿形层次遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回锯齿形层次遍历如下:
[
[3],
[20,9],
[15,7]
]
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
# 层次遍历,使用队列
res = []
if not root:
return res
queue = [root]
row = 1
while queue:
line_res = []
queue_size = len(queue)
# 当前队列节点向四周扩散
for i in range(queue_size):
curNode = queue.pop(0)
# 划重点: 判断是否到达终点
line_res.append(curNode.val)
if curNode.left:
queue.append(curNode.left)
if curNode.right:
queue.append(curNode.right)
if row % 2 == 0:
# line_res = sorted(line_res, reverse = True) 按元素排序,出错
line_res.reverse()
# line_res = line_res[::-1]
print(line_res)
row += 1
res.append(line_res)
return res
6. leetcode-101. 对称二叉树-简单
101. 对称二叉树
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
# 非递归 方法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
# 非递归: BFS判断当前层元素是否为对称
# 时间复杂度:
# 空间复杂度:
res = []
if not root:
return True
queue = [root]
row = 1
while queue:
line_res = []
queue_size = len(queue)
# 将当前队列元素向四周扩散
for i in range(queue_size):
curNode = queue.pop(0)
# 划重点: 判断是否到达终止
if curNode:
line_res.append(curNode.val)
queue.append(curNode.left)
queue.append(curNode.right)
else:
line_res.append('null')
# 判断当前层是否符合镜像二叉树要求
if len(line_res) % 2 != 0 and row != 1:
return False
back = line_res[::-1]
if line_res != back:
return False
row += 1
return True
# 递归方法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isMirror(self,t1,t2):
if not t1 and not t2:
return True
if not t1 or not t2:
return False
return t1.val == t2.val and self.isMirror(t1.right,t2.left) and self.isMirror(t1.left,t2.right)
def isSymmetric(self, root: TreeNode) -> bool:
return self.isMirror(root,root)
7.leetcode-200.岛屿数量-中等
200. 岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
大佬解答1-DFS + BFS + 并查集(Python 代码、Java 代码)
说明:以下介绍的算法,除了并查集以外,DFS 和 BFS 都属于很基础的算法内容,也非常好理解,写法也相对固定,读者需要多写,发现并记录自己的问题,我也是在写了几遍甚至是在写本题解的过程中,才发现出自己的问题。
这道题是可以使用一个经典的算法来解决的,那就是 Flood fill,以下的定义来自 维基百科:Flood fill 词条。
Flood fill 算法是从一个区域中提取若干个连通的点与其他相邻区域区分开(或分别染成不同颜色)的经典 算法。因为其思路类似洪水从一个区域扩散到所有能到达的区域而得名。在 GNU Go 和 扫雷 中,Flood Fill算法被用来计算需要被清除的区域。
“Flood” 我查了一下,作为动词是 “淹没;充满” 的意思,作为名词是 “洪水” 的意思。下面我们简单解释一下这个算法:
从一个区域中提取若干个连通的点与其他相邻区域区分开
从一个点扩散开,找到与其连通的点,这不是什么高深的算法,其实就是从一个点开始,进行一次 “深度优先遍历” 或者 “广度优先遍历”,通过 “深度优先遍历” 或者 “广度优先遍历” 发现一片连着的区域,对于这道题来说,就是从一个是 “陆地” 的格子开始进行一次 “深度优先遍历” 或者 “广度优先遍历”,把与之相连的所有的格子都标记上,视为发现了一个 “岛屿”。
说明:这里做 “标记” 的意思是,通过 “深度优先遍历” 或者 “广度优先遍历” 操作,我发现了一个新的格子,与起始点的那个格子是连通的,我们视为 “标记” 过,也可以说 “被访问过”。
那么每一次进行 “深度优先遍历” 或者 “广度优先遍历” 的条件就是:
1、这个格子是陆地 1,如果是水域 0 就无从谈论 “岛屿”;
2、这个格子不能是之前发现 “岛屿” 的过程中执行了 “深度优先遍历” 或者 “广度优先遍历” 操作,而被标记的格子(这句话说得太拗口了,大家意会即可,意会不了不是您的问题,是我表达的问题,直接看代码会清楚很多)。
方法一:深度优先遍历
方法二:广度优先遍历
除了 “深度优先遍历”,你还可以使用 “广度优先遍历”,此时你就不用回溯了。“广度优先遍历” 需要一个 “辅助队列”。
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
![]()

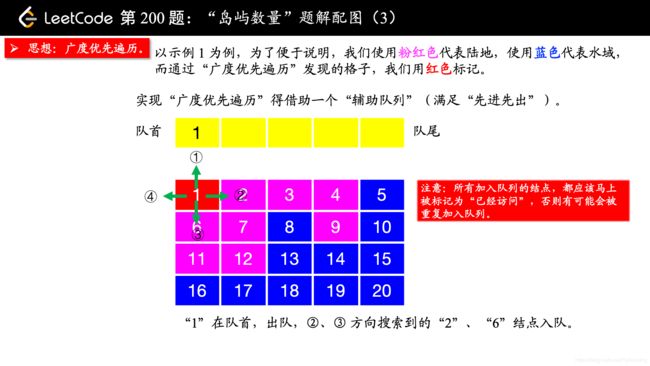
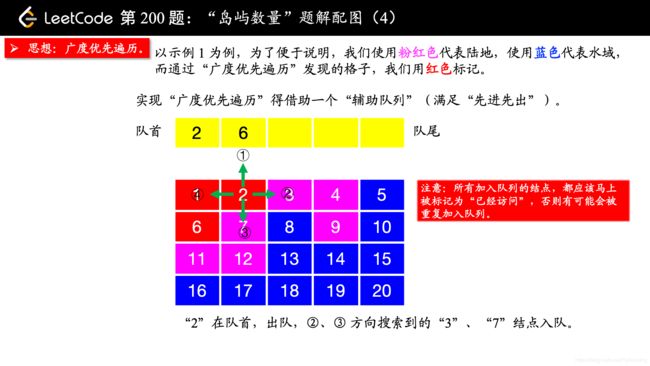
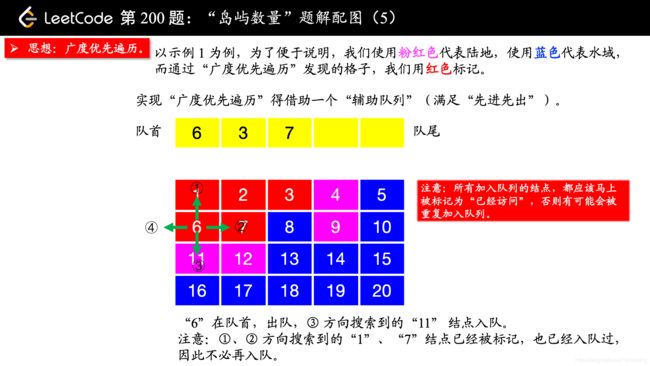
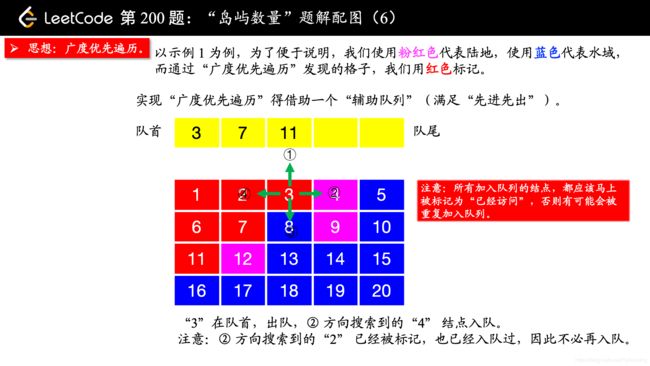
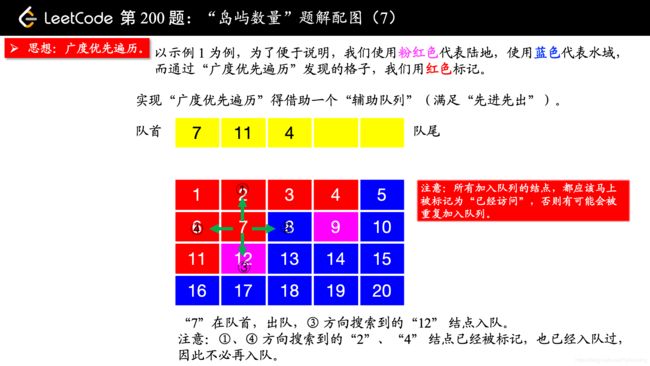
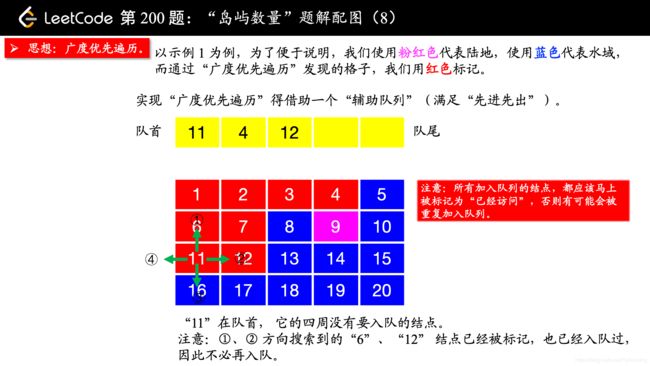
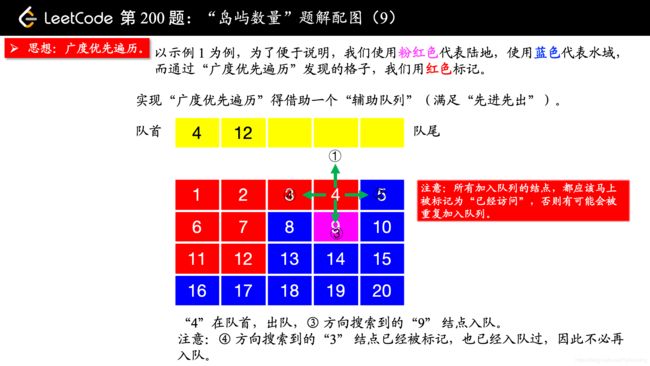
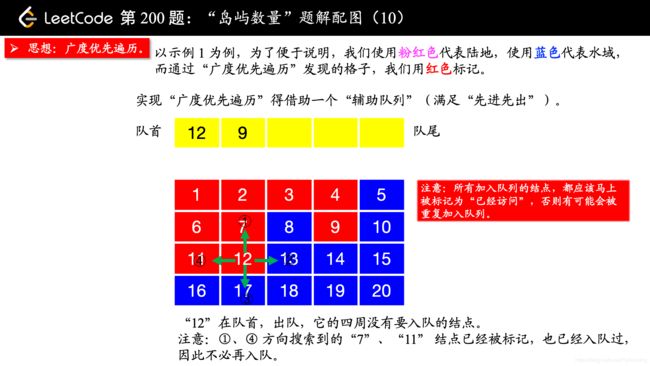
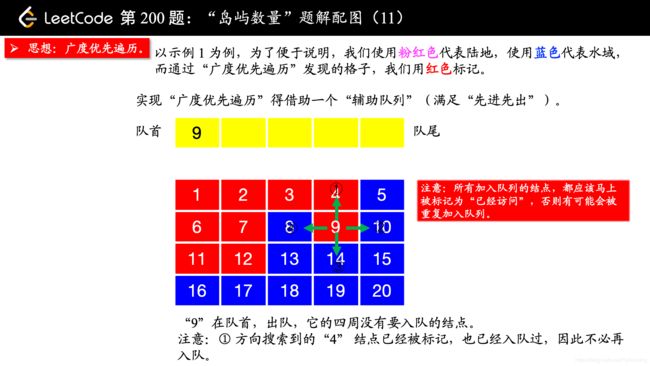
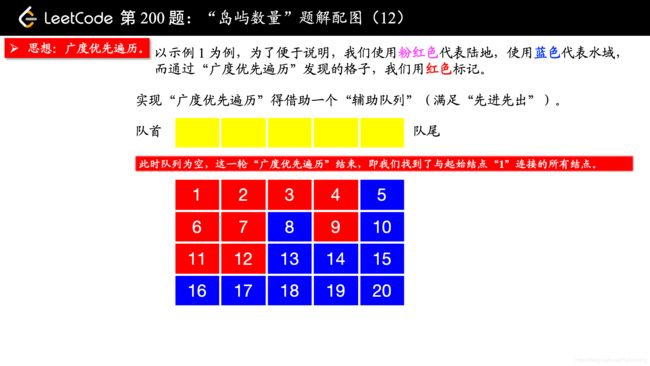
在写 “广度优先遍历” 的时候,要注意一点:
所有加入队列的结点,都应该马上被标记为 “已经访问”,否则有可能会被重复加入队列。
我一开始在编写的时候,等到队列出队的时候才标记 “已经访问”,事实上,这种做法是错误的。因为如果不在刚刚入队列的时候标记 “已经访问”,相同的结点很可能会重复入队,如果你遇到“超时”的提示,你不妨把你的队列打印出来看一下,就很清楚看到我说的这一点。
大佬代码:
from typing import List
from collections import deque
class Solution:
# x-1,y
# x,y-1 x,y x,y+1
# x+1,y
# 方向数组,它表示了相对于当前位置的 4 个方向的横、纵坐标的偏移量,这是一个常见的技巧
directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]
def numIslands(self, grid: List[List[str]]) -> int:
m = len(grid)
# 特判
if m == 0:
return 0
n = len(grid[0])
marked = [[False for _ in range(n)] for _ in range(m)]
count = 0
# 从第 1 行、第 1 格开始,对每一格尝试进行一次 DFS 操作
for i in range(m):
for j in range(n):
# 只要是陆地,且没有被访问过的,就可以使用 BFS 发现与之相连的陆地,并进行标记
if not marked[i][j] and grid[i][j] == '1':
# count 可以理解为连通分量,你可以在广度优先遍历完成以后,再计数,
# 即这行代码放在【位置 1】也是可以的
count += 1
queue = deque()
queue.append((i, j))
# 注意:这里要标记上已经访问过
marked[i][j] = True
while queue:
cur_x, cur_y = queue.popleft()
# 得到 4 个方向的坐标
for direction in self.directions:
new_i = cur_x + direction[0]
new_j = cur_y + direction[1]
# 如果不越界、没有被访问过、并且还要是陆地,我就继续放入队列,放入队列的同时,要记得标记已经访问过
if 0 <= new_i < m and 0 <= new_j < n and not marked[new_i][new_j] and grid[new_i][new_j] == '1':
queue.append((new_i, new_j))
#【特别注意】在放入队列以后,要马上标记成已经访问过,语义也是十分清楚的:反正只要进入了队列,你迟早都会遍历到它
# 而不是在出队列的时候再标记
#【特别注意】如果是出队列的时候再标记,会造成很多重复的结点进入队列,造成重复的操作,这句话如果你没有写对地方,代码会严重超时的
marked[new_i][new_j] = True
#【位置 1】
return count
if __name__ == '__main__':
grid = [['1', '1', '1', '1', '0'],
['1', '1', '0', '1', '0'],
['1', '1', '0', '0', '0'],
['0', '0', '0', '0', '0']]
solution = Solution()
result = solution.numIslands(grid)
print(result)
自己python再次实现一次(基本抄大佬)
class Solution:
# x-1,y
# x,y-1 x,y x,y+1
# x+1,y
# 方向数组,它表示了相对于当前位置的 4 个方向的横、纵坐标的偏移量,这是一个常见的技巧
directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]
def numIslands(self, grid: List[List[str]]) -> int:
# 求岛屿数量: 将二维网格看作图, 本质上是搜索满足条件的点。
# 怎样识别使用BFS? 搜索邻接岛屿
# BFS框架
# res = []
# queue = [root] // 队列数据结构
#
# // 使用队列进行遍历
# while queue:
# queue_size = len(queue)
#
# // 将当前队列元素向四周扩散
# for i in range(queue_szie):
# curNode = queue.pop(0)
#
# // 划重点: 判断是否到达终止位置
# if curNode is target:
# return step
# ...
#
# // 当前节点相邻节点添加
# for (Node x in curNode.adj()):
# // 去除已经访问等干扰因素
# if Node x not in visited:
# queue.append(x)
# visited.append(x)
# // 划重点: 更新步数
# step += 1
'''
grid list: 待搜索图
return num : 岛屿数量
'''
# 边界处理: grid:[]
if not grid:
return 0
rows, cols = len(grid), len(grid[0])
# marked: 类似于 visited, 用来标注 坐标是否访问过
marked = [[False for _ in range(cols)] for _ in range(rows)]
count = 0
# 由于 start、target都未知, 所有节点都可能为 start, 所以需要遍历整个网格,选择start
# 从第一行、第一格 开始, 对每一个格子尝试进行一次 BFS 操作
for row in range(rows):
for col in range(cols):
# 只要是 陆地(value=1), 且未被访问过的, 就可以使用 BFS 发现与之相连的陆地, 并进行标记
if not marked[row][col] and grid[row][col] == '1':
# count 可以理解为联通分量, 可以在 BFS 遍历完成之后(【位置1】),再计数,也可以在此处(必定有一个结果)
# // 进入 BFS的标准化模板
queue = [(row, col)]
# 注意这里要标记已经访问过
marked[row][col] = True
# 利用队列进行遍历
while queue:
# queue_size: 本质作用, 记录一步或者一层 队列中有几个元素; 如果结果不结算层、不计算多少步, 其实也没必要的;
queue_size = len(queue)
# 划重点: 将当前队列中的所有节点向四周
for i in range(queue_size):
curNode = queue.pop(0)
curNode_x, curNode_y = curNode
# print(curNode_x, curNode_y)
# 划重点: 判断是否到达终止条件, 本题终止为: 队列中元素为空
# 划重点: 当前节点的相邻节点加入, 记得判断是否访问, 能不能访问
for direction in self.directions:
new_row = curNode_x + direction[0]
new_col = curNode_y + direction[1]
# print('new_row, new_col', new_row, new_col)
# 如果1) 不越界; 2) 未被访问; 3) 为 陆地; 继续放入队列, 放入队列同时标注: 已访问过
if 0<=new_row本题一些新的启发、创新
1. BFS搜索中 start、target均未知, 需要遍历 grid网格中所有点, 从当前点作为 start进行BFS;
2. BFS中计数问题: 每次BFS必有一个结果;
3. BFS框架中 队列中元素数量统计是为了 记录当前层、当前行、当前步骤 , 如果问题中不涉及,可以不考虑,最终遍历完 队列queue就行;
4. visited列表、marked 网格grid都是必不可少的,代码可读性会很强;
5. directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]向四个方向遍历相邻节点的学习
8.leetcode-542. 01 矩阵-中等-未AC
9.leetcode-1162. 地图分析-中等-未AC
自己一些思路和思考
1. 典型网格问题 BFS, start节点可以有很多,
2. 没想明白最大距离怎么计算?
10. 涂色问题、连通块问题、01宫格问题、全排列问题
11.leetcode-695. 岛屿的最大面积-中等-AC
695. 岛屿的最大面积-
给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
示例 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ,因为岛屿只能包含水平或垂直的四个方向的 1 。
示例 2:
[[0,0,0,0,0,0,0,0]]
对于上面这个给定的矩阵, 返回 0。
大佬参考代码
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
if not grid:
return 0
areas = []
visit = [[0 for _ in range(len(grid[0]))] for __ in range(len(grid))]
steps = [[1, 0], [0, -1], [-1, 0], [0, 1]] # 四个方向走
def BFS(x, y):
area = 1
queue = [(x, y)]
visit[x][y] = 1
while queue:
p = queue.pop(0)
for i in steps:
dx, dy = p[0] + i[0], p[1] + i[1]
if 0 <= dx < len(grid) and 0 <= dy < len(grid[0]) and grid[dx][dy] == 1 and visit[dx][dy] == 0:
visit[dx][dy] = 1
area += 1
queue.append((dx, dy))
areas.append(area)
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 1 and visit[i][j] == 0:
BFS(i, j)
return max(areas) if areas else 0
自己按照大佬思路实现
class Solution:
# 套路: 沿着四个方向遍历
directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
# 经典BFS, 同样问题, start可以是任意节点; 保留各个 queue搜索到的 max(areas)
if not grid:
return 0
# res: 记录每次搜索到的岛屿面机
res = []
rows, cols = len(grid), len(grid[0])
visited = [[False for _ in range(cols)] for _ in range(rows)]
# BFS框架
def BFS(start_x, start_y):
area = 1
queue = [(start_x, start_y)]
visited[start_x][start_y] = True
# 开始使用队列遍历
while queue:
queue_size = len(queue)
# 划重点: 将队列元素向四周扩散
for i in range(queue_size):
curNode = queue.pop(0)
curNode_x, curNode_y = curNode
# 划重点: 判断是否终止
# 划重点: 当前节点相邻节点加入队列
for direction in self.directions:
new_row = curNode_x + direction[0]
new_col = curNode_y + direction[1]
# 新节点进行条件判断
# 如果: 1)不越界; 2) 土地; 3)未被访问; 继续放入队列,并且标注已访问
if 0<=new_row12. 剑指 Offer 13. 机器人的运动范围-中等-自己AC
剑指 Offer 13. 机器人的运动范围
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,
它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。
例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],
因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
自己首先思路
1. 简单BFS题目, 且给定起点 start , 难点在于 限制条件的理解;
class Solution:
# 网格BFS周围套路
directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]
def sumBit(self, x, y):
s = list(map(str,[x,y])) #将a,b移入列表中
s1 = list(map(int,list(s[0])))
s2 = list(map(int, list(s[1])))
return sum(s1) + sum(s2)
def movingCount(self, m: int, n: int, k: int) -> int:
# 思路: BFS搜索一次结果;
# 套模板就行
if m <= 0 or n <= 0 or k < 0:
return 0
# 初始化grid, visited
grid = [[0 for _ in range(n)] for _ in range(m)]
visited = [[False for _ in range(n)] for _ in range(m)]
queue = [(0, 0)]
visited[0][0] = True
res = 1
while queue:
queue_size = len(queue)
# 划重点: 当前队列元素向四周扩散
for i in range(queue_size):
curNode = queue.pop(0)
curNode_x, curNode_y = curNode
# 划重点: 判断是否到达终止条件
# 划重点: 将当前队列节点 相邻节点加入队列
for direction in self.directions:
new_row = curNode_x + direction[0]
new_col = curNode_y + direction[1]
# 判断节点的可行性
# 1) 不越界; 2) 未访问; 3) 满足 数位之和小于K
if 0<=new_row13. leetcode-733. 图像渲染-简单
有一幅以二维整数数组表示的图画,每一个整数表示该图画的像素值大小,数值在 0 到 65535 之间。
给你一个坐标 (sr, sc) 表示图像渲染开始的像素值(行 ,列)和一个新的颜色值 newColor,让你重新上色这幅图像。
输入:
image = [[1,1,1],[1,1,0],[1,0,1]]
sr = 1, sc = 1, newColor = 2
输出: [[2,2,2],[2,2,0],[2,0,1]]
解析:
在图像的正中间,(坐标(sr,sc)=(1,1)),
在路径上所有符合条件的像素点的颜色都被更改成2。
注意,右下角的像素没有更改为2,
因为它不是在上下左右四个方向上与初始点相连的像素点。
python- BFS、DFS
class Solution:
def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
# 思路1: BFS
# 思路2: DFS, 本质依然是找最大联通面积
directions = [(-1, 0), (1, 0), (0, 1), (0, -1)]
def BFS(image, sr, sc, newColor, originColor):
# 初始化queue
queue = [(sr, sc)]
image[sr][sc] = newColor
while queue:
queue_len = len(queue)
# 换重点: 队列中元素像四周扩散
for i in range(queue_len):
curNode = queue.pop(0)
curNode_row, curNode_col = curNode
# 划重点: 终止条件判断
# 划重点: 当前节点向 邻居扩散
for direction in directions:
new_row = curNode_row + direction[0]
new_col = curNode_col + direction[1]
# 合法性判断: 1) 不越界; 2) 未访问; 3) 等于orginCol
if 0<=new_row1293. 网格中的最短路径
- python实现:
class Solution:
def shortestPath(self, grid: List[List[int]], k: int) -> int:
# 思路: BFS, 但是对于具体障碍的清除没想清楚;
directions = [(-1, 0), (1, 0), (0, 1), (0, -1)]
m, n = len(grid), len(grid[0])
if m == 1 and n == 1:
return 0
k = min(k, m+n-3)
visited = set([0, 0, k])
queue = [[0, 0, k]]
step = 0
while queue:
queue_len = len(queue)
print(queue)
# 当前queue中元素分别向四周扩散
for i in range(queue_len):
curNode = queue.pop(0)
curNode_x, curNode_y, rest = curNode
# 终止条件
if curNode_x == m-1 and curNode_y == n - 1:
return step
# 当前节点向四周进行扩散;
for direction in directions:
new_x = curNode_x + direction[0]
new_y = curNode_y + direction[1]
# 队列加入元素合法性判断: 1) 不越界;
if 0<=new_x0 and (new_x, new_y, rest-1) not in visited:
queue.append((new_x, new_y, rest-1))
visited.add((new_x, new_y, rest-1))
# 这时候看看具体怎么需要,走一步算一步可能放这了。
step = step + 1
return -1
DFS-大佬总结框架
一. DFS-
算法框架
例题1:
例题2:
DFS-相关题目
1.leetcode-200.岛屿数量-中等
200. 岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
大佬解答1-DFS + BFS + 并查集(Python 代码、Java 代码)
方法一:深度优先遍历
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
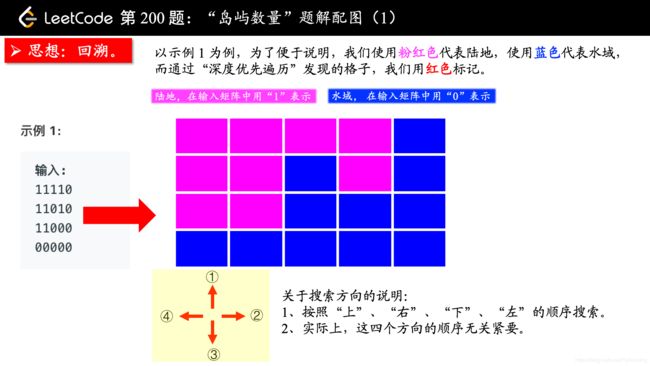
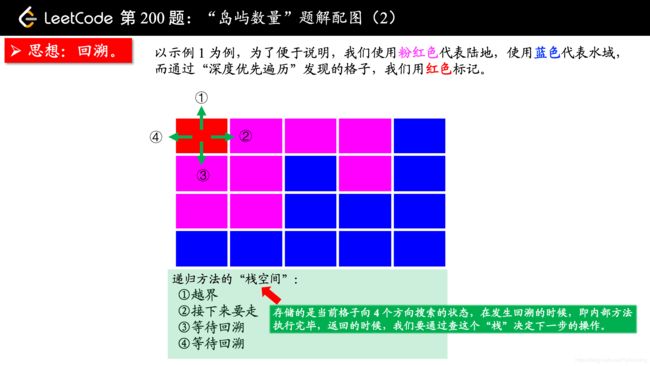
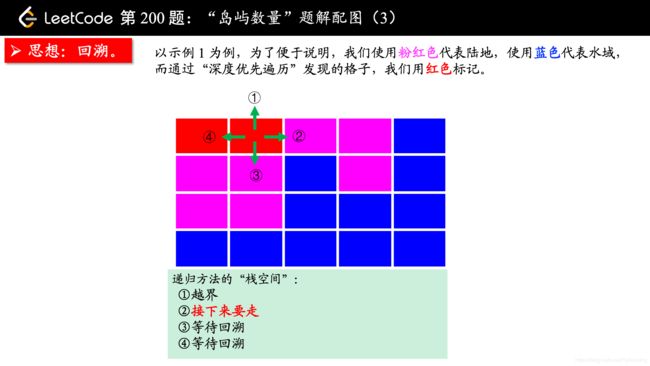
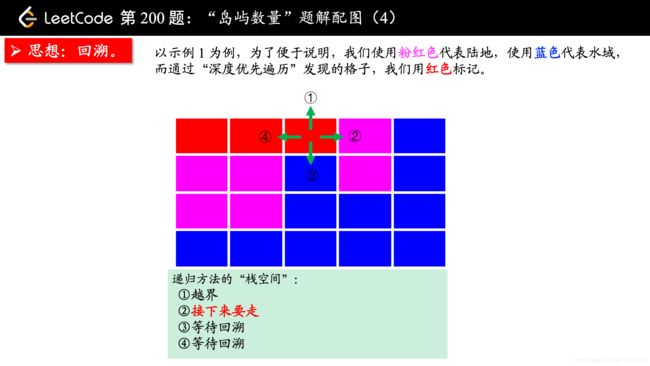
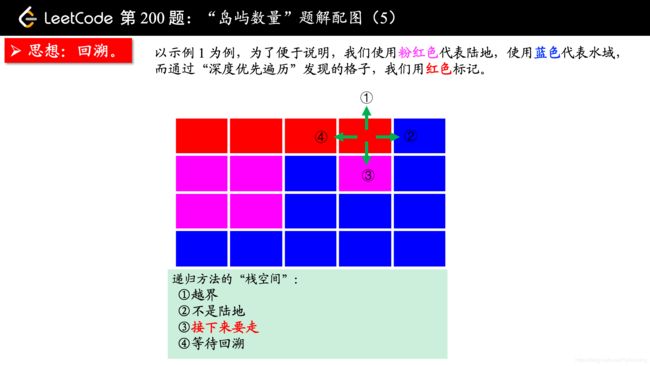
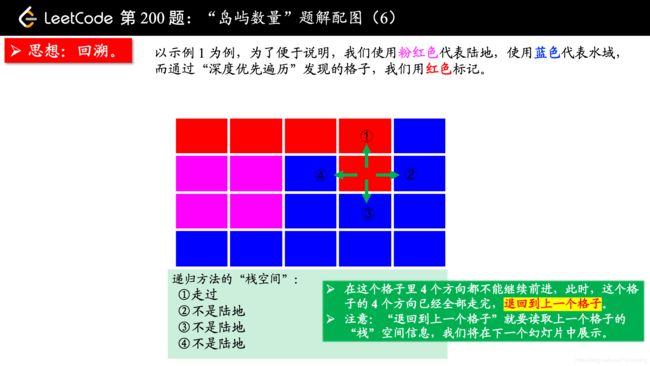
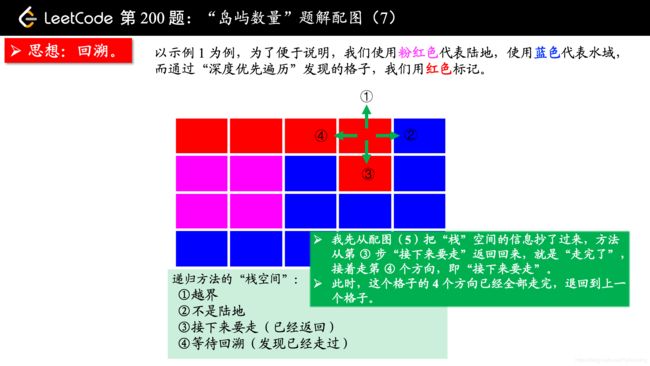
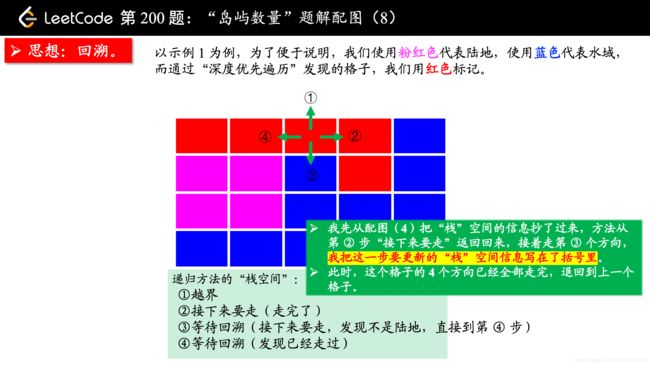
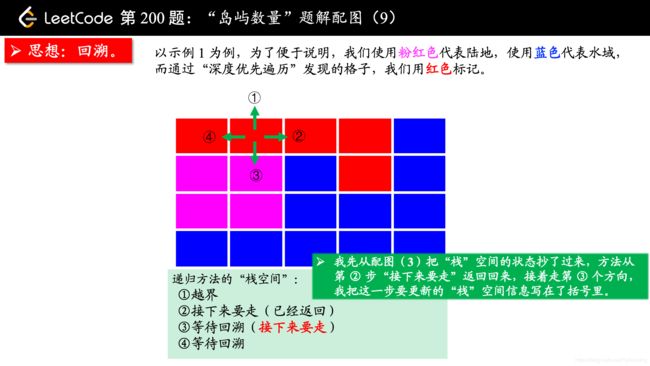
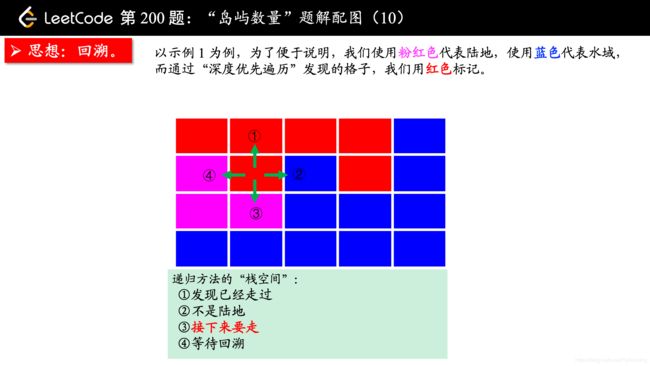
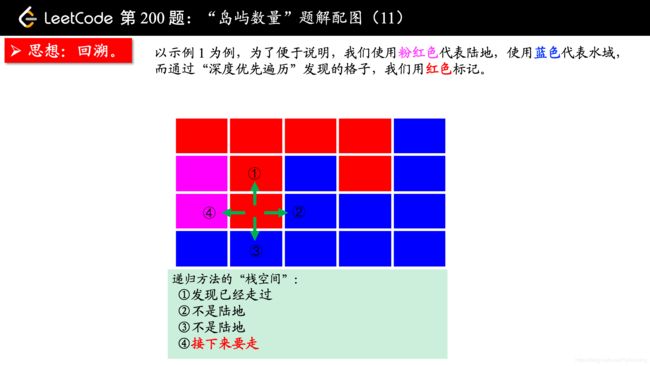
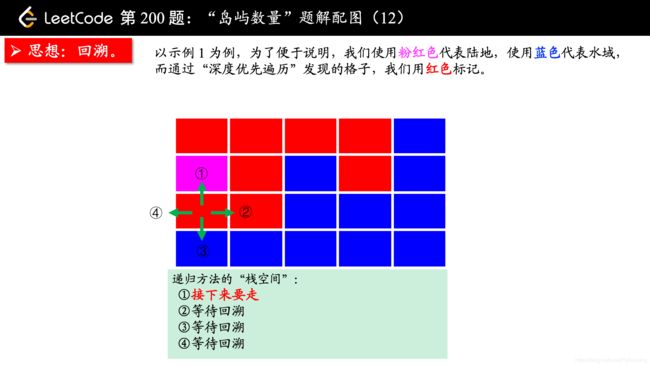
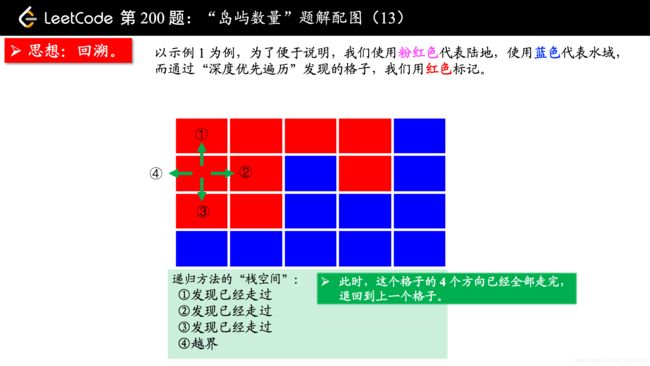
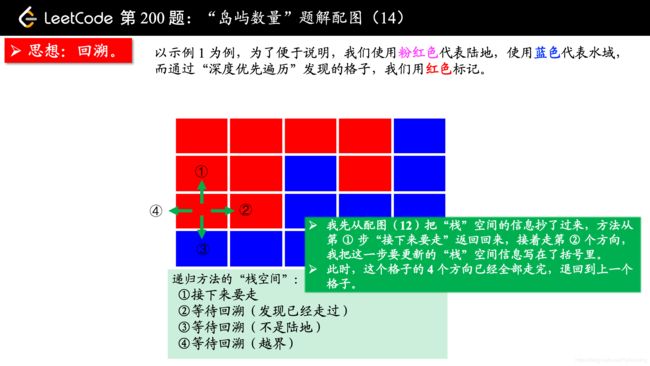
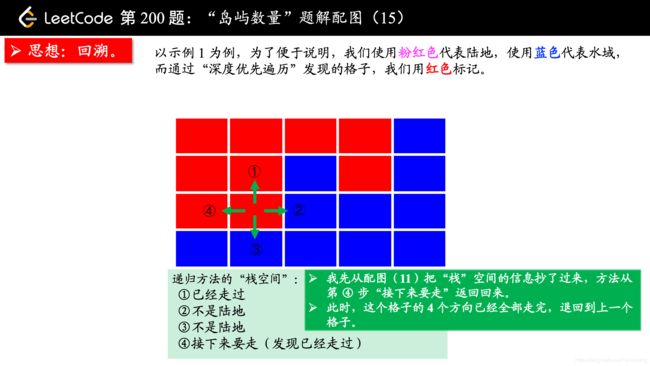
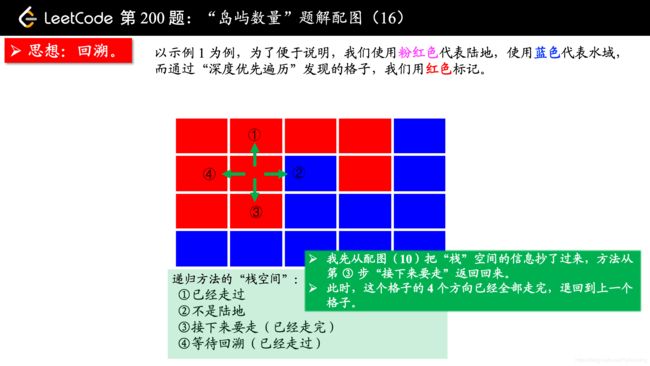
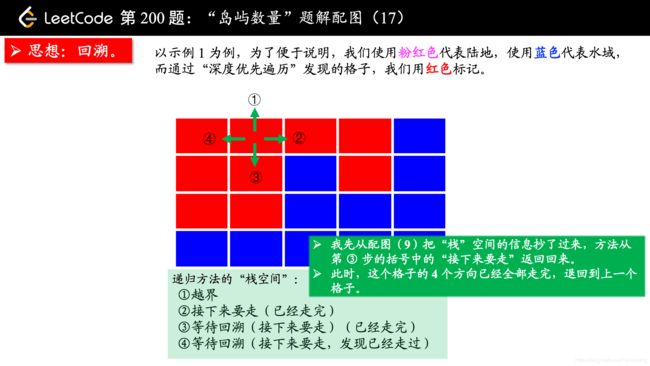
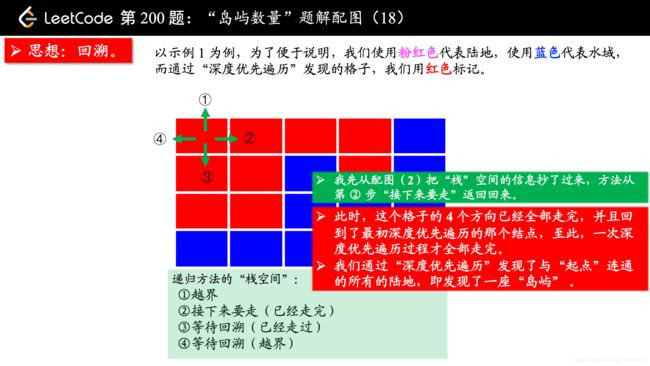
参考大佬代码:
from typing import List
class Solution:
# x-1,y
# x,y-1 x,y x,y+1
# x+1,y
# 方向数组,它表示了相对于当前位置的 4 个方向的横、纵坐标的偏移量,这是一个常见的技巧
directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]
def numIslands(self, grid: List[List[str]]) -> int:
m = len(grid)
# 特判
if m == 0:
return 0
n = len(grid[0])
marked = [[False for _ in range(n)] for _ in range(m)]
count = 0
# 从第 1 行、第 1 格开始,对每一格尝试进行一次 DFS 操作
for i in range(m):
for j in range(n):
# 只要是陆地,且没有被访问过的,就可以使用 DFS 发现与之相连的陆地,并进行标记
if not marked[i][j] and grid[i][j] == '1':
# count 可以理解为连通分量,你可以在深度优先遍历完成以后,再计数,
# 即这行代码放在【位置 1】也是可以的
count += 1
self.__dfs(grid, i, j, m, n, marked)
# 【位置 1】
return count
def __dfs(self, grid, i, j, m, n, marked):
marked[i][j] = True
for direction in self.directions:
new_i = i + direction[0]
new_j = j + direction[1]
if 0 <= new_i < m and 0 <= new_j < n and not marked[new_i][new_j] and grid[new_i][new_j] == '1':
self.__dfs(grid, new_i, new_j, m, n, marked)
if __name__ == '__main__':
grid = [['1', '1', '1', '1', '0'],
['1', '1', '0', '1', '0'],
['1', '1', '0', '0', '0'],
['0', '0', '0', '0', '0']]
solution = Solution()
result = solution.numIslands(grid)
print(result)
自己python再次实现一次(基本抄大佬)