2017WHU校赛color

“e起来编程”（武汉网络赛） 2017年4月9号。 12：30-17：50.
http://acm.whu.edu.cn/olive/problem/639
题目链接
http://acm.whu.edu.cn/

Color

#####Input file: standard input#####
#####Output file: standard output#####
#####Time limit: 1 second#####
#####Memory limit: 512 mebibytes#####
When Asuho was just a little girl, she has been loving stars, as there are so many romantic stories about old legends and the stars.

Today, as usual, Asuho went to the observatory with her beloved boyfriend, Kogasaka Ming, to see the splendid sky of galaxy. Sitting with Kogasaka shoulder to shoulder, Asuho thought nothing could make her happier.

“Asuho,” Kogasaka called Asuho softly. “I have a question about the Hoshizora(night sky with stars).”

“What’s it?” Asuho answered, happily. “I know everything about the stories, you can ask anything.”

Kogasaka smiled, “You see the stars? Just imagine there are nn distinct stars in the sky while n-1n−1 relationships connect them. Each relationship is between two stars and all stars are connected directly or indirectly. Now you need to divide the nn stars into mm different types. Beware that no two directly connected stars should share the same type and some stars cannot be some types. I want you to tell me how many distinct solutions there could be.”

Suddenly the Stella meteor shower appeared, so the lovers forgot the question and started to admire the beautiful Hoshizora.

Asuho thought it was unbelievable that Kogasaka should ask her such a foolish question which she can’t solve. Of course she didn’t wish to reveal her poor math. So can you help her to tell the answer?

###Input###
The Input file contains several test cases.

For each case, the first line contains two integers $n\left(2\le n\le 10^4\right),m(1\le m\le 20)$

The next $n-1$ lines, each line contains 2 integers $x_i,y_i$ expressing relationships between the two stars.

The next $n$ lines, each lines contains m numbers and each of the mm is 0 or 1.

The $i$-th number of the $j$-th line respect whether $j$-th star can be divided into the $i$-th type. 1 means it could while 0 means not.

###Output###
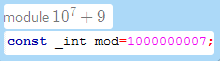
For each test case, output one single line, containing the number of solutions module $10^7+9$

###Examples###
####Input 1####
4 6
1 2
1 3
1 4
1 1 1 1 1 0
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
####Output 1####
625

题目大意：
balabala说着这么多。（1）其实就是告诉你现在有n颗星星m种颜色，（2）然后给你n-1条边，连接这些星星，变成一个无向无环图（树型结构）。（3）每颗星星都有m种颜色中的几种，接下来n行的第i行就代表第i颗星星的m种颜色中第几种颜色是否可用（分别用0、1表示）。
问：（1）在相邻星星颜色不同的情况下，（2）每个星星染一种颜色，（3）共有多少种染色方案？

--------------------分隔线-------------------

思路：
一开始没有意识到这就是树型DP，就在那瞎搞，最初推得是使树的父节点每种颜色的方案数向下推到子节点中存在且和父节点不同的颜色中，并使所有最下层所有叶子节点的方案数相乘（发现并不对,GG，然后去上英语课去了T T）。在上英语课的时候突然想到了反过来推，由子节点推向父节点，并产生了正解。但是由于某些原因wrong了一页，对拍都拍不出来。

题解：
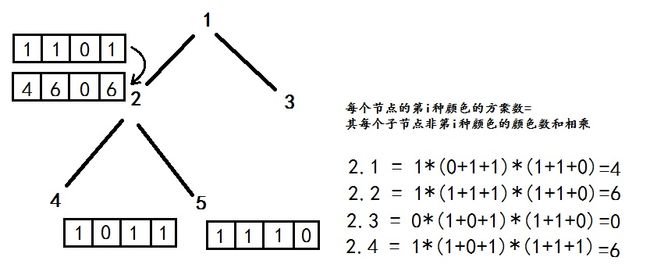
用DFS的方式搜，从下至上求出每个父节点的方案数，最终根节点的方案数就是所有方案数。父节点的某种颜色（颜色A）的方案数就等于其子节点除去颜色A的所有其他颜色方案数的和（Si）的乘积。（例如ABCD四种颜色且拥有k个子节点的父节点，其A颜色方案数计算方法：$$S_{(father)A}=(S{1}_B+S{1}_C+S{1}_D)\ast (S{2}_B+S{2}_C+S{2}_D)\ast ...\ast (S{i}_B+S{i}_C+S{i}_D)\ast ...\ast (S{k}_B+S{k}_C+S{k}_D)$$）
这样就产生了一个新的问题。搜索的时候怎么判断这个节点所连接的某节点是其父节点还是其子节点。额，用一个数组记录某节点属于树的哪一层就好了。
DFS搜到叶子节点直接返回给其父节点，然后层层递归得出根节点每种颜色的方案数，相加即可。

图解：

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define eps 0.00000001
#define pi acos(-1,0)
#define pr 999983
#define _int long long
#define inf 1000000000
using namespace std;
struct point {
    int x,y;
    int b[25];
    bool operator < (const point &a) const {
        return x>a.x;
    }
};
priority_queue <point> que;

const _int mod=10000009;

vector <int> vec[10100];
int b[10100];
_int a[10100][25];
int n,m;

int fun(int x){

    int ceng;
    ///vector::iterator it;
    for(vector<int>::iterator it=vec[x].begin();it!=vec[x].end();it++){
        if (b[*it]!=0) ceng=b[*it];
        //cout<<*it<
    }

    for(vector<int>::iterator it=vec[x].begin();it!=vec[x].end();it++){
        if (b[*it]==0){
            b[*it]=ceng+1;
            fun(*it);
        }
        //cout<<*it<
    }

    for (int i=0; i<=m; i++){
        if (a[x][i]!=0){
            for(vector<int>::iterator it=vec[x].begin();it!=vec[x].end();it++){
                if (b[*it]==ceng+1){
                    _int temps=0;
                    for (int k=0; k<m; k++){
                        if (k!=i) temps=temps+a[*it][k];
                        temps=temps%mod;
                    }

                    a[x][i]=a[x][i]*temps;
                    a[x][i]=a[x][i]%mod;
                }
                //cout<<*it<
            }
        }
    }
    return 0;
}

int main() {
    int T;
    while (~scanf("%d%d",&n,&m)){
        for (int i=1; i<=n; i++){
            vec[i].clear();
        }
        memset(b,0,sizeof(b));
        memset(a,0,sizeof(a));

        int vecx,vecy;
        for (int i=1; i<n; i++){
            scanf("%d%d",&vecx,&vecy);
            vec[vecx].push_back(vecy);
            vec[vecy].push_back(vecx);
        }
        for (int i=1; i<=n; i++){
            for(int j=0; j<m; j++){
                scanf("%lld",&a[i][j]);
            }
        }

        b[1]=1;
        fun(1);

        _int sum=0;
        for (int i=0; i<m; i++){
            sum=sum+a[1][i];
            sum=sum%mod;
        }
        printf("%lld\n",sum);
    }
    return 0;
}

//    freopen("1.in","r",stdin);
//    freopen("1.out","w",stdout);
/*
7 4
1 2
1 3
1 4
2 5
2 6
2 7
1 1 1 1
1 0 1 1
1 0 1 0
0 1 0 1
1 1 1 1
1 0 1 0
0 0 1 0
*/

Wrong两天的原因