【论文阅读】行人重识别算法优化技巧:Bags of Tricks and A Strong Baseline for Deep Person Re-identification
论文原文 - Bags of Tricks and A Strong Baseline for Deep Person Re-identification
现有baseline对比
作者在Market1501和DukeMTMC-reID数据集上对比了ECCV2018和CVPR2018的一些baseline的性能,并与自己提出的baseline进行对比。
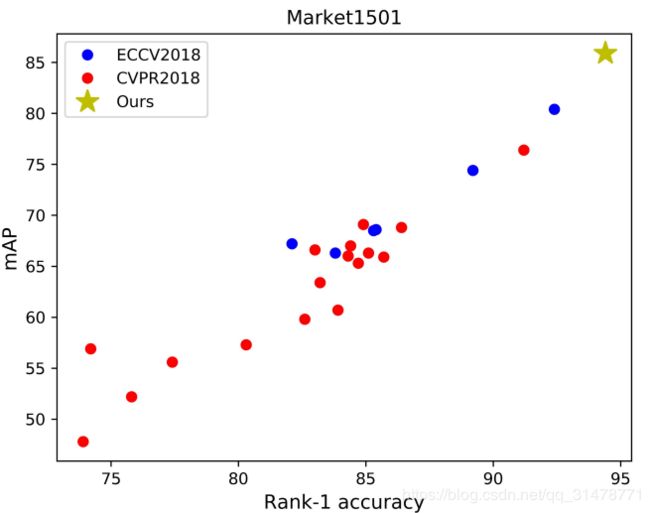
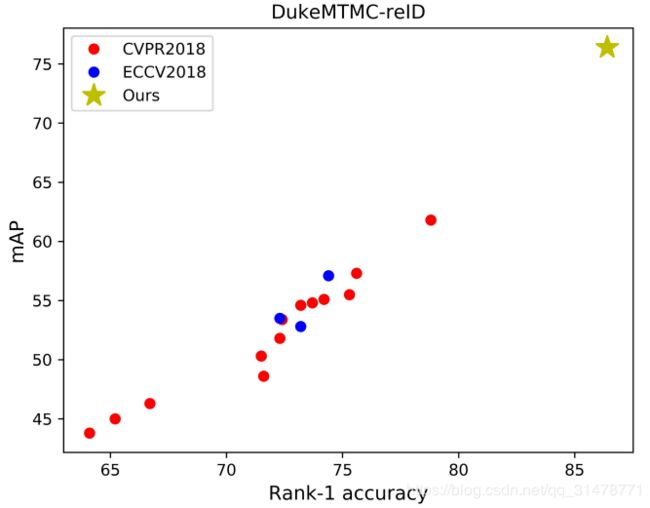
大多数baseline都比较弱,在Market1501上23个baseline中只有2个的top1准确率超过了90%,而有4个低于80%;DukeMTMC-reID数据集上则所有baseline的top1准确率都没有超过80%。有些文章改进的方式并不是方法本身,而是训练的技巧,但是训练技巧在文章中却轻描淡写的带过,让读者很容易错过这些信息,这会夸大了论文中方法的重要性。
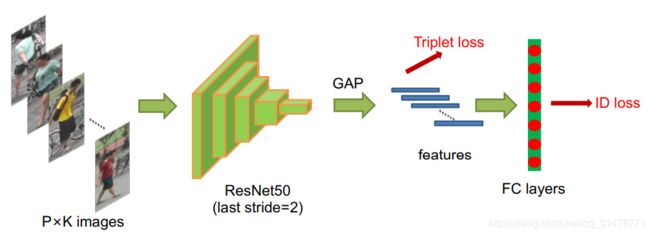
标准Baseline
- 使用一个带有ImageNet预训练参数的ResNet50,并改变最后一层FC层的输出维度为训练集行人的ID数目。
- 随机采样P个身份以及每个人的K幅图片,构成一个batch,batchsize=P×K。文章中设置的P=16,K=4。将图片resize到256×128像素大小,并进行10个像素的zero-padding,接着随机crop成256×128矩形样本,以此进行数据增强。
- 进行概率0.5的随机翻转,并进行归一化处理,RGB通道分别减去均值0.485,0.456,0.406,并分别除以0.229,0.224,0.225。
- 模型输出的ReID特征f用于计算triplet loss,triplet loss的margin设置为0.3。ID预测值用于计算交叉熵损失。
- 使用Adam方法进行优化,初始学习率设置为3.5e-4。在第40和70个epoch时,学习率缩小为原来的10%,共训练120个epoch。
训练技巧
学习率变化(Warm up)策略
学习率对行人重识别模型的影响很大,初始的学习率一般都设得比较大,但有人提出Warm up的策略对行人重识别模型更有效。具体的操作方法是将初始的学习率设置得很小,然后慢慢增大至预设的学习率,如下图红色曲线。

公式可表示为:
l r ( t ) = { 3.5 × 1 0 − 5 × t 10 if t ≤ 10 3.5 × 1 0 − 4 if 10 < t ≤ 40 3.5 × 1 0 − 5 if 40 < t ≤ 70 3.5 × 1 0 − 6 if 70 < t ≤ 120 l r(t)=\left\{\begin{array}{ll}{3.5 \times 10^{-5} \times \frac{t}{10}} & {\text { if } t \leq 10} \\ {3.5 \times 10^{-4}} & {\text { if } 10<t \leq 40} \\ {3.5 \times 10^{-5}} & {\text { if } 40<t \leq 70} \\ {3.5 \times 10^{-6}} & {\text { if } 70<t \leq 120}\end{array}\right. lr(t)=⎩⎪⎪⎨⎪⎪⎧3.5×10−5×10t3.5×10−43.5×10−53.5×10−6 if t≤10 if 10<t≤40 if 40<t≤70 if 70<t≤120
随机擦除数据扩展
这是一种常见的分类问题数据增强方式,对行人检测效果明显。使用该方法能有效降低遮挡问题带来的影响,提高模型的鲁棒性。

随机抽取一张图片,每张图片被选中的概率为 p e p_{e} pe。对于图像I,随机选择一块矩形区域 I e I_{e} Ie,大小为 ( W e , H e ) \left(W_{e}, H_{e}\right) (We,He),将该区域的像素值设置为图像I的像素均值。作者使用的超参数设置为 p = 0.5 , 0.02 < S e < 0.4 , r 1 = 0.3 , r 2 = 3.33 p=0.5,0.02<S_{e}<0.4, r_{1}=0.3, r_{2}=3.33 p=0.5,0.02<Se<0.4,r1=0.3,r2=3.33。随机擦除后图像效果如下。

标签平滑
标签平滑也是分类问题中使用的一种技巧。假设网络分类数为 N N N, y y y为某一样本真实的ID标签, p i p_{i} pi是第i类的预测概率。交叉熵损失函数计算如下:
L ( I D ) = ∑ i = 1 N − q i log ( p i ) { q i = 0 , y ≠ i q i = 1 , y = i L(I D)=\sum_{i=1}^{N}-q_{i} \log \left(p_{i}\right)\left\{\begin{array}{l}{q_{i}=0, y \neq i} \\ {q_{i}=1, y=i}\end{array}\right. L(ID)=i=1∑N−qilog(pi){qi=0,y̸=iqi=1,y=i因为测试集中出现的行人ID不会出现在训练集中,所以需要防止模型过拟合训练数据中的ID。标签的形式通常是one-hot编码的形式,也就是 q i q_{i} qi只会取0和1两个值。标签平滑的思想是对真实标签进行改造,使其不再是one-hot编码。
q i = { 1 − N − 1 N ε if i = y ε / N otherwise q_{i}=\left\{\begin{array}{ll}{1-\frac{N-1}{N} \varepsilon} & {\text { if } i=y} \\ {\varepsilon / N} & {\text { otherwise }}\end{array}\right. qi={1−NN−1εε/N if i=y otherwise 其中 ε \varepsilon ε是一个很小的常量,来降低模型在训练集上的置信度,作者设置 ε = 0.1 \varepsilon=0.1 ε=0.1。
假设 N = 5 , ε = 0.1 N=5,\varepsilon=0.1 N=5,ε=0.1,真实标签为[1, 0, 0, 0],经过标签平滑后变成了[0.92, 0.02, 0.02, 0.02],这样进行优化是模型输出的预测标签与真实标签总会存在损失,从而降低了过拟合的风险。
移除最后一个降采样操作(Last Stride)
有人发现在backbone网络中移除最后一个降采样操作, 提升了特征图的尺寸以此丰富特征的粒度。ResNet50中的原本最后一个卷积层的步幅(stride)为2,当输入一张256×128的样本,ResNet50网络输出的特征图尺寸大小为8×4。如果将最后一个卷积层的步幅从2改为1,可以得到尺寸为16×8空间大小的特征图。这样在仅仅增加了微小的计算量,并且没有引入更多的需要训练的参数条件下,能带来明显的性能改善。
BNNeck
在训练行人重识别模型时,通常会使用同时ID loss和Triplet loss,但是两种loss函数的目标并不协调。在行人重识别中,ID loss使用余弦距离进行优化比欧式距离更加合适,而Triplet loss则更加注重在欧式空间中提高类内紧凑型和类间可分性。因此,二者关注的度量空间不一致,这可能会导致出现当一个loss减小时,另一个loss振荡或增大的现象。

为解决上述问题,作者提出了BNNeck。BNNeck仅仅在特征层和FC分类层之间增加了一个BN层。网络原先提取的特征为 f t f_{t} ft,通过BN层后变为 f i f_{i} fi。在训练阶段,分别用 f t f_{t} ft和 f i f_{i} fi来计算Triplet loss与ID loss。
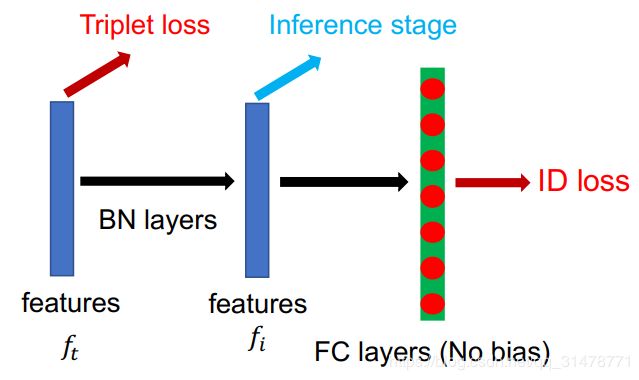
由于 f i f_{i} fi经过了正则化,ID loss更容易收敛。此外,BNNeck减少了ID loss对 f t f_{t} ft优化的限制,使得Triplet loss同时更容易收敛。由于超平面相对于原始坐标来说几乎是对称的,BNNeck的另外一个作用是去除分类FC层的偏差。

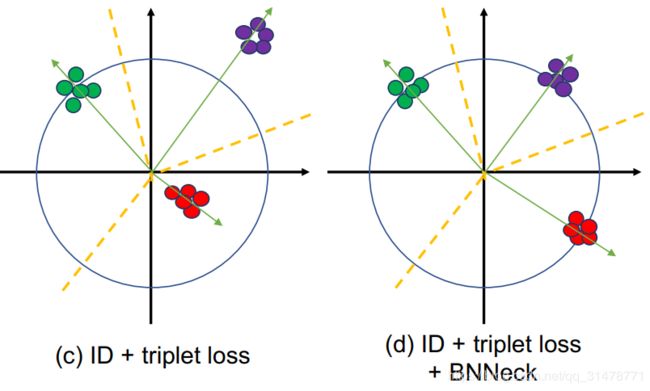
Center Loss
Triplet loss计算公式为:
L T r i = [ d p − d n + α ] + L_{T r i}=\left[d_{p}-d_{n}+\alpha\right]_{+} LTri=[dp−dn+α]+其中, d p d_{p} dp和 d n d_{n} dn分别表示正样本对与负样本对的特征距离, α \alpha α是Triplet loss的margin。然而Triplet loss只考虑 d p d_{p} dp和 d n d_{n} dn的差别,不考虑它们的绝对值。例如,当 d p = 0.3 , d n = 0.5 d_{p}=0.3, d_{n}=0.5 dp=0.3,dn=0.5时,Triplet loss为0.1;当 d p = 1.3 , d n = 1.5 d_{p}=1.3, d_{n}=1.5 dp=1.3,dn=1.5时,Triplet loss也是0.1。因此很难保证在整个训练数据集中 d p < d n d_{p}<d_{n} dp<dn。
为了使类内更加紧凑,作者又加入了人脸识别中提出的Center Loss,它在学习到一个类中心的同时,将深度特征的距离与他们对应的类中心作为惩罚项,这可以弥补Triplet loss的缺点。Center Loss公式为:
L C = 1 2 ∑ j = 1 B ∥ f t j − c y j ∥ 2 2 \mathcal{L}_{C}=\frac{1}{2} \sum_{j=1}^{B}\left\|\boldsymbol{f}_{t_{j}}-\boldsymbol{c}_{y_{j}}\right\|_{2}^{2} LC=21j=1∑B∥∥∥ftj−cyj∥∥∥22其中, c y j c_{y_{j}} cyj表示深度特征第 y j y_{j} yj个类的中心, B B B是batchsize。将三种loss相加,一起优化整个网络:
L = L I D + L T r i p l e t + β L C L=L_{I D}+L_{T r i p l e t}+\beta L_{C} L=LID+LTriplet+βLC β β β是Center Loss的平衡权重,作者将 β β β设置成了0.0005。
修改后的baseline
对比测试
同数据域每个trick的效果
作者首先在同一个数据域下进行试验,在Market1501和DukeMTMC-ReID数据集上面分别测试了每个trick的效果。每个trick都能有效提升识别准确性,其中REA、BNNeck涨幅比较明显的。

跨数据域每个trick的效果
为了展示这些trick的鲁棒性和泛化能力,作者还做了跨数据域的实验,即在一个数据集上训练,在另外一个数据集上测试。结果显示REA会大大降低跨域的性能,其他的trick都还是有一定程度的提升。最后删除REA,只使用其他五个trick,M→D的结果达到了41.4的rank1。目前M→D的SOTA方法也就50左右的水平,这已经是个不错的Baseline了。当然也值得深思,为什么REA数据增广会降低跨域性能。

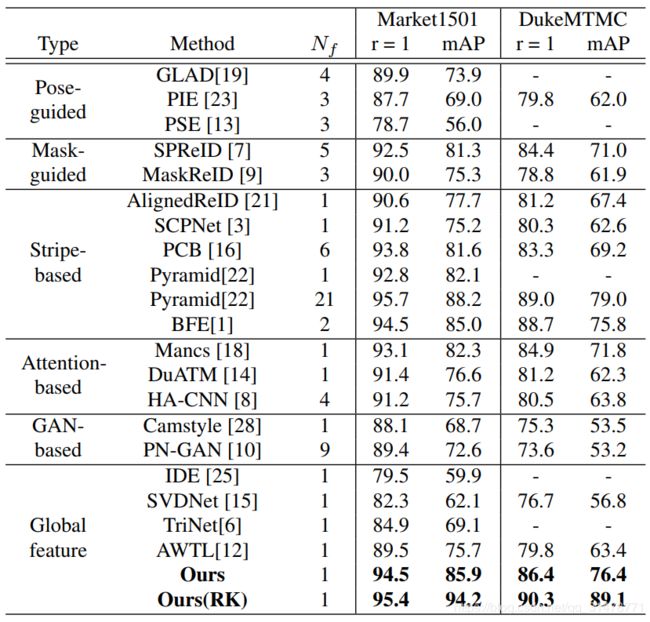
和State-of-the-Arts的方法进行比较
作者把baseline的结果直接和SOTA的方法进行比较,除了少数几个能够达到95+的结果以外,其他方法的结果均低于改进的baseline。值得一提的是,本文只是使用一个简单global feature,加了一层BN而已。目前主流能够达到93+的方法都concatenate多个local feature。腾讯的金字塔结构更是融合21个不同尺度的local feature。在所有只使用一个global feature的方法里,该方法的性能是大大领先的,而且训练代价非常小,就是加了一些trick而已。
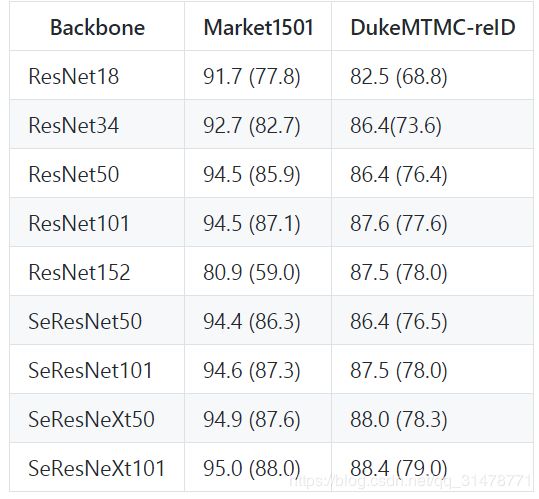
Backbone扩展
对Backbone网络进行了扩展,包括ResNet、SENet、SeResNet等等。大致结果呈现网络越深,效果越好,这也符合正常的结论。其中SeResNeXt101取得了95%的rank1和88%的mAP,基本已经相当高了。可能是Market1501数据集太小,并且比较简单,使用ResNet152训练有些过拟合了。