Reinforcement Learning强化学习系列之二:MC prediction
引言
这几个月一直在忙找工作和毕业论文的事情,博客搁置了一段时间,现在稍微有点空闲时间,又啃起了强化学习的东西,今天主要介绍的是强化学习的免模型学习free-model learning中的最基础的部分蒙特卡洛方法(Monte Carlo),并以21点游戏作为说明。
本文主要参考的文献是[1]参考的主要代码是这位斯坦福大神的课程代码,本系列的文章均不作为商用,如有侵权请联系我的邮箱
Monte Carlo Learning
在前一篇文章中介绍了基于模型的强化学习方法,对于很多现实问题,其实环境的state和状态转移概率是未知的,因此在计算Value的时候不能按照基于模型的方法进行全概率展开,这也是免模型学习的难点所在。很自然的对于很多数学问题,如果不能直接求解,采样的方法是个替代的方法,比如重要性采样。
在蒙特卡洛(MC)的强化学习中,MC并不是特指某个具体的方法,只是单纯指的是基于随机采样的方法进行计算学习。本节主要讲的是通过MC计算Value的方法。
对于某种策略 π π ,我们从起始状态 s0 s 0 出发,根据该策略获取状态的轨迹:
这里 at a t 表示 t t 时刻的动作, rt r t 表示的 t t 时刻的reward。我们把每一个这种采样的序列成为一个时期episode,表示一个事件从开始到结束,通过采样多个episode,我们可以得到多个状态序列。
在MC prediction中,计算Value函数有两种方法,第一种是first-visit,第二种是evert-visit,其中first-visit在计算 Value(st) V a l u e ( s t ) 值的时候是对于在每个episode中,选取该episode第一次出现状态 st s t 以后的序列reward值来计算 value(st) v a l u e ( s t ) ,然后对所有的episode中的 value(st) v a l u e ( s t ) 按照出现次数取平均值,就可以得到 value(st) v a l u e ( s t ) ,算法可以表示如下:

对应的every-visit则返回的是每次 st s t 以后的序列reward值,然后在全部的episode里面取平均值,本文中使用的是first-visit MC prediction.
21点游戏
这一小节打算[1]书中使用21点游戏为背景,对于两个人,游戏规则是这样:
- 有两种角色,庄家和玩家
- 扑克有1-10,J,Q,K,其中J,Q,K表示数值10,卡牌1(Ace)可以表示1也可以表示11
- 在最开始,玩家发两张牌,庄家发两张牌,其中庄家的牌一张是公开的,玩家两张牌都是不公开的,只有玩家自己才能看到。
玩家可以选择要牌,可以决定手中的1表示的是1还是表示11,如果玩家在开始的时候是一张1一种10(10,J,Q,K)那么表示是natural,此时如果庄家也是natural那么表示的是平局,反之则玩家胜,如果在玩家要牌的过程中手中牌的总数大于21,那么就爆了,玩家输,如果玩家没要爆并停止要牌,那么庄家开始要牌,庄家在点数小于17的时候必须要牌,如果超过了17那么就要停止要牌,庄家在要牌的过程中爆了则庄家输,如果庄家停牌并没有爆,那么这个时候庄家和玩家开牌,谁的点数更靠近21点便胜利,如果相等则平局。
游戏分析:
在最开始,如果玩家手中的点数小于11那么必然会要牌直到超过11点
- 每个人手中如果1可以在不爆的情况下可以表示为11,那么必然会当做11
根据以上分析,那么在游戏过程中,玩家手中的总和应该在12-21之间,而庄家公开的牌是1-10,不管庄家的1表示的11还是1,而玩家手中的1可以表示1或者11,当玩家表示为1的时候表示是no usable,当玩家表示为11的时候表示为usable,那么显然所有的state状态又200个。
游戏建模假设:
- 牌是无限发的,因此玩家和庄家不可以通过桌面上公开的牌进行猜测剩下的牌的概率
游戏建模
对于以上分析,我们可以建立一个21点游戏的背景代码:
#coding=utf-8
import numpy as np
deck = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 10, 10, 10]
np.random.seed(3)
#random choice a card from deck
def draw_card():
choice = np.random.randint(0,len(deck))
return deck[choice]
#choose two card at the begining
def draw_hand():
return [draw_card(),draw_card()]
#define whether player or dealer has a usable ace
def usable_ace(hand):
return (1 in hand) and (sum(hand)+10<=21)
#define the total sum of hand
def sum_hand(hand):
if usable_ace(hand):
return sum(hand)+10
else:
return sum(hand)
#whether bust
def is_bust(hand):
return sum_hand(hand)>21
def score(hand):
return 0 if is_bust(hand) else sum_hand(hand)
#whether natural
def is_natural(hand):
return hand==[1,10]
def cmp(a,b):
return int(a>b)-int(aclass Blackjack(object):
def __init__(self,natural=False):
self.natural = natural
self.nA=2
self._reset()
def observation(self):
return (sum_hand(self.player),self.dealer[0],usable_ace(self.player))
def _reset(self):
self.dealer = draw_hand()
self.player = draw_hand()
while sum_hand(self.player)<12:
self.player.append(draw_card())
return self.observation()
def _step(self,action):
"""
:param action: 1 means hit, 0 means stick
:return:
"""
done=False
if action:
self.player.append(draw_card())
if is_bust(self.player):
done=True
reward=-1
else:
done = False
reward = 0
else:
done=True
while(sum_hand(self.dealer)<17):
self.dealer.append(draw_card())
reward = cmp(score(self.player), score(self.dealer))
if self.natural and is_natural(self.player) and reward == 1:
reward = 1.5
return self.observation(),reward,done
假设我们选取的策略是当玩家点数超过20的时候就停止要牌,反之则要牌,那么使用first-visit MC prediction的时候代码如下:
#coding=utf-8
from Blackjack import Blackjack
from collections import defaultdict
import sys
import matplotlib
import os
import plotting
matplotlib.style.use('ggplot')
def sample_policy(observation):
player_sum,dealer_show_hand,usable_ace=observation
if player_sum<20:
return 1
return 0
#
# episode.append(state)
# if return_sum.has_key(state):
# return_sum[state]+=reward
# else:
# return_sum[state]=reward
# if return_count.has_key(state):
# return_count[state]+=1
# else:
# return_count=1
# if V.has_key(state):
# V[state]
def mc_prediction(policy,env,num_episodes,discount=1.0):
"""
first-visit mc prediction
:param env: blackjack env
:param policy: initial policy
:param num_episodes:
:param discount:
:return:
"""
return_sum = defaultdict(float)
return_count = defaultdict(float)
V = defaultdict(float)
for i_episode in range(1,1+num_episodes):
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes))
sys.stdout.flush()
env._reset()
state = env.observation()
episode=[]
#sample using given policy
for i in range(100):
action = policy(state)
next_state,reward,done = env._step(action)
episode.append((state,action,reward))
if done:
break
else:
state=next_state
seperate_episode = set([tuple(eps[0]) for eps in episode])
for s_eps in seperate_episode:
#find the first visit state
for i,x in enumerate(episode):
if x[0] == s_eps:
first_visit_pos=i
G = sum([e[2]*discount**idx for idx,e in enumerate(episode[first_visit_pos:])])
return_sum[s_eps]+=G
return_count[s_eps]+=1.0
V[s_eps] = return_sum[s_eps]*1.0/return_count[s_eps]
return V
env = Blackjack()
V_10k = mc_prediction(sample_policy, env, num_episodes=10000)
plotting.plot_value_function(V_10k, title="10,000 Steps")
V_500k = mc_prediction(sample_policy, env, num_episodes=500000)
plotting.plot_value_function(V_500k, title="500,000 Steps")
当使用10000个episode的时候可以得到的是如下图:
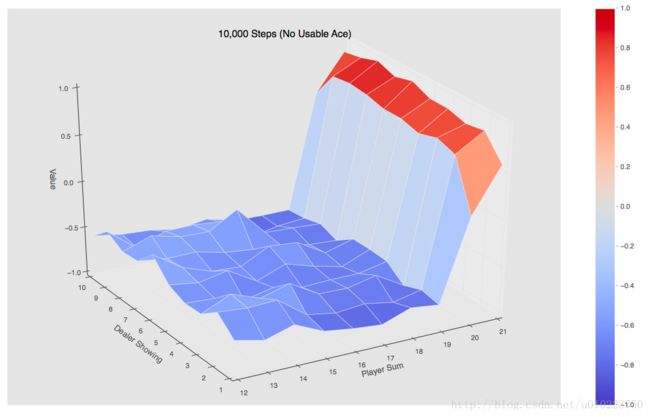

当使用500000个episode的时候可以得到的是如下图:
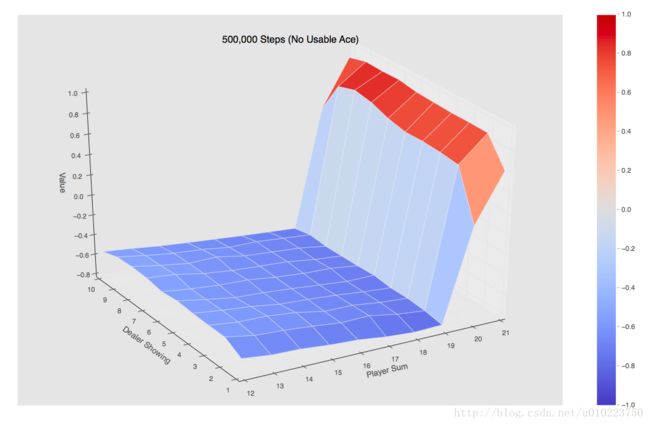

可以看出的是,手中有usable的整个Value值还是要高一点。
代码可以在这里获取
后记
今天主要介绍的是MC prediction,以21点游戏为例,下面的文章将会介绍MC control以及 on-policy以及off-policy的一些内容,记于北京。