腾讯2016春招模拟笔试题 —— 编程题(3道)
写在前面的话~
春招 + 模拟笔试 【C++研发】
模拟笔试时间是 2016-03-25 21:30 ~ 22:30
试题主要包括两部分:不定项选择 + 编程 分别计时 时间都是30分钟。(逃~。。。
前面的不定项选择15道 大部分都是往年的题 所以我基本上15分钟就提交了。。。(然~。。。
编程题有三道 印象中前两道好像也是往年的题 第三道以前见过 (但。。。
不思考 30分钟三道题完全不够用。 第三道题基本上就要20分钟
很显然 前两道 10分钟
最后一道 写了一大半 然后就没有然后 被自动提交 提交。。。
还有现在的OJ怎么不给调试了。。没有测试用例了。。
唉 不说了~
-------------------我是分割线----------------------------
上题目(只记得题目大意了 大家将就看哈~):
第一题(n位格雷码)
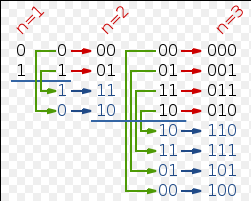
在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同, 则称这种编码为格雷码(Gray Code),请编写一个函数,使用递归的方法生成N位的格雷码。
给定一个整数n,请返回n位的格雷码,顺序为从0开始。
1
返回:["0","1"]
分析:
首先需要知道格雷码 n位格雷码最后返回2^n个元素。
另外,注意题意要求用递归求解。
上个图(from WIKI) 代码的思路可参考该图。
Leetcode上也有一道题89. Gray Code可以做一下。
代码如下:
vector getGray(int n)
{
vector v;
if(n == 1)
{
v.push_back("0");
v.push_back("1");
return v;
}
else
{
vector v = getGray(n - 1);
int vSize = v.size();
vector v2;
for(int i = 0; i < vSize; i++)
{
if(i % 2 == 0)
{
v2.push_back(v[i]+"0");
v2.push_back(v[i]+"1");
}
else
{
v2.push_back(v[i]+"1");
v2.push_back(v[i]+"0");
}
}
return v2;
}
} 第二题(微信红包)
春节期间小明使用微信收到很多个红包,非常开心。在查看领取红包记录时发现,某个红包金额出现的次数超过了红包总数的一半。请帮小明找到该红包金额。写出具体算法思路和代码实现,要求算法尽可能高效。
给定一个红包的金额数组gifts及它的大小n,请返回所求红包的金额。
[1,2,3,2,2],5
返回:2分析:
使用哈希当然可以求解,但并不是最优的。
这道题最优的解法类似 《编程之美》中"寻找水王"的问题,复杂度为 O(n) O(1)。
设定一个辅助变量cnt 记录元素出现的次数 假设出现次数大于一半的元素为 target 。
在遍历数组元素的过程中,如果元素与target不等,那么cnt--,否则cnt++;
当cnt<0时,说明目前找到的target肯定不是最终的结果 同时更新target为当前遍历到元素。
最终遍历完数组 剩下的那个就是要找的目标target。
【注:这里需要注意的是 上面这个思路只能确定出现次数最多的元素 但并不一定是出现次数
超过一半的数,因此一定要验证一下 否则测试用例不能全部通过】。
代码如下:
int getValue(vector gifts, int n) {
if (n <= 0) return 0;
int vSize = gifts.size();
int res = -1, cnt = 0;
for(int idx = 0; idx < vSize; ++idx)
{
if (cnt == 0)
{
res = gifts[idx];
cnt++;
}
if (gifts[idx] != res) cnt--;
else cnt++;
}
// 这里最好验证一下
// 如果某个数字出现次数最多 但是并没有出现超过总数一半
cnt = 0;
for (int i = 0; i < vSize; i++)
{
if (gifts[i] == res) cnt++;
}
return (cnt > vSize/2) ? res : 0;
}
第三题(大数乘法)
大数乘法题。
给出2个大整数num1, num2,计算num1*num2的结果。
【大数的长度不超过1000 且 > 0(?) 原谅我不太记得是不是大于0】
下面的代码按大于0处理。。
分析:
如果是java 自带了大数类 BigInteger 代码不超过10行。。。
(也贴一下代码 个人不太擅长java)
import java.util.Scanner;
import java.math.BigInteger;
public class Main
{
public static void main(String args[])
{
Scanner cin = new Scanner(System.in);
BigInteger a, b;
while (cin.hasNext())
{
a = cin.nextBigInteger();
b = cin.nextBigInteger();
System.out.println(a.multiply(b).toString());
}
}
}【高端的FFT求解大数问题不在这里的讨论范围】
我们可以模拟乘法实现的过程。
比如:123 * 456
6 分别与3 2 1 相乘。
接着是
5 与 3 2 1相乘。
4 与 3 2 1相乘。
代码如下:
#include
#include
#include
using namespace std;
string big_number_multiply(string a, string b)
{
int a_len = a.length(), b_len = b.length(), len = a_len + b_len;
vector c(a_len + b_len, 0);
len = a_len + b_len;
for (int i = 0; i < b_len; ++i)
{
for (int j = 0; j < a_len; ++j)
{
c[i + j] += (b[b_len - i - 1] - '0') * (a[a_len - j - 1] - '0');
}
}
string res;
res.resize(len);
int inc = 0; // 进位
for (int i = 0; i < len; ++i)
{
c[i] += inc;
inc = c[i] / 10;
c[i] %= 10;
res = (char)(c[i] + '0') + res;
}
if (inc != 0)
{
res = (char)(inc + '0') + res;
}
// 最高位为0 需要去除
int idx = 0;
while (res[idx] == '0') idx++;
return res.substr(idx, res.size());
}
int main(void)
{
string s1, s2;
cin >> s1 >> s2;
cout << big_number_multiply(s1, s2) << endl;
return 0;
}