【深度强化学习】交叉熵方法

前言

重读《Deep Reinforcemnet Learning Hands-on》， 常读常新， 极其深入浅出的一本深度强化学习教程。 本文的唯一贡献是对其进行了翻译和提炼， 加一点自己的理解组织成一篇中文笔记。

原英文书下载地址: 传送门
原代码地址： 传送门

第四章 交叉熵方法

在本章中， 我们将完成本书的第一部分， 并介绍一种强化学习方法——交叉熵。 尽管没有一些其他许多强化学习方法知名：例如 deep Q-learning （DQN），或者 Advantage Actor-Critic。 但它仍具有自己的强项：

• 简洁： 这个算法非常简洁， 在pytorch中的实现不超过100行代码。
• 很好的收敛性：在不需要 学习开发 复杂的多步策略 且 回合较短奖励频繁 的 简单环境中， 交叉熵法行之有效。 尽管这种场景不一定常见， 但交叉熵法真的非常适合。

接下来，我们会先从实际使用方面介绍交叉熵， 阐释他如何应用于两种Gym环境（一种是熟悉的CartPole， 一种是FrozenLake）。最后，我们介绍其理论原理。 理论部分是可选的， 且需要较好的数理统计知识。 但如果你想理解交叉熵方法， 就值得深入一看。

强化学习方法的分类

强化学习的方法，可以从多个角度进行分类：

• Model-free 或 Model-base
  Model-free 方法指的是， 该强化学习方法并不需要对环境或奖励建立一个专门的模型进行分析。 它只是直接地把动作和环境联系在一起。 简单来说： Agent只是将当前的观测通过一些计算， 得出应该采取的动作。 相反的， model-based 方法， 尝试去预测 下一个观测 和（或）奖励， 并根据这一预测， 来选择可能最佳的动作。 两种方法都有其优点或缺点， 但一般model-base的方法只能用于确定性的环境中，比如有严格规则的棋类游戏。 而model-free方法则更容易被训练， 因为复杂的观测很难被简单建模。 本书中讨论的几乎全都是model-free方法， 这也是过去几十年最活跃的领域。
• Value-based 或 policy-base
  Policy-based 方法指的是agent提出策略——每一步应该采取怎样的动作。 一般而言， policy用一个表示概率分布的向量代表——每个值代表对应的action被采用的概率。 相反的， value-based 方法，指的是agent会计算出每个action的对应value， 并选择value最高的action。这两种方法都非常普遍，并在书的后面章节详细介绍。
• On-policy 或 off-policy
  这个概念会在以后详细介绍， 现在我们只需要知道：off-policy是指从旧的历史数据中学习到的方法 (历史数据指的是比如 由之前的agent得到的数据， 或者人工演示的记录或者是同一个agent之前几个回合 的数据）。

按这个分类，交叉熵方法属于 model-free, policy-based, on-policy 的 强化学习方法：

• 并不对环境进行任何建模。 只是简单地告诉agent每步该采取的策略。
• 输出的是一个策略（动作选取的概率分布）
• 需要环境的最新数据

实用的交叉熵

对交叉熵的讲述分为两部分： 理论 和 实践。 实践部分是更直观的， 而理论部分解释了其为何得以运作。

你也许还记得， 强化学习中 最重要的东西就是 agent， agent的目的是争取在与环境的交互中（action）为了获得尽可能多的奖励积累。在实践中， 我们用通过的机器学习方法来实现agent——接收观测值， 转化成输出。 具体的输出则视具体使用的方法而定 （比如policy-based方法， 或者value-based方法）。而我们当前要介绍的policy-based方法 是 policy-based， 也就是说，我们会用一个非线性函数（神经网络）来产生 策略 (policy），示意图可以参考如下：

即神经网络接受观测s， 输出策略pi， 这里神经网络就是扮演了Agent的角色。

在实践中， 策略 往往 表示为 每个动作的概率分布， 这就与 经典的分类问题非常相像——输出样例属于每个类别的概率分布。 那么我们的Agent的工作就非常简单理解了： 接收观测环境值给神经网络， 获得动作的概率分布（策略），再根据概率采用，选取动作。

接下来，再介绍强化学习中很重要的一个概念 ： 经验 (experience)。每一场进行的游戏（一个回合，episode）就是一条经验， 可以用于神经网络的学习（优化）。 每个回合，包括了一系列步， 每一步中包括了：环境的观测， 采用的动作及当前步的reward。对于每个episode，我们都可以计算他的总reward——根据前几章的介绍，这里我们可以定义一个决定agent短视与否的gamma折扣系数。 在本例中，我们假定gamma=1，即agent关心的是所有步的reward之和。 那么，我们的经验池可以描述为下图：

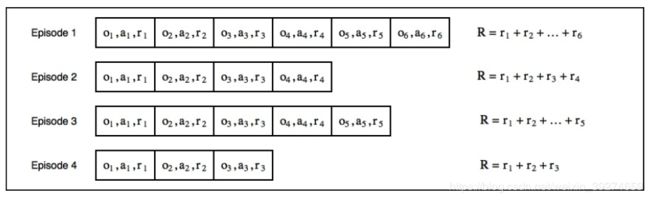
o1,a1,r1分别代表了第一步的观测，动作和奖励。 我们agent的目的是使得总reward R 最大化。 显然，由于我们一开始只是随机的策略， 每个episode的奖励值大小不同。 而我们的策略就是， 用表现更好的episode作为“经验”，对 网络进行训练。 因此， 交叉熵法的核心步骤可以概括如下：

1. 在选定的环境中，进行N个独立的回合，并记录。
2. 计算总的reward值。
3. 丢弃总reward值后70%的回合经验。 （70%可以自己修改为任意比例）
4. 使用剩下的30%的“精英经验”， 以观测值为输入， 训练网络的输出与该观测值对应的动作值接近。 （很容易理解， 我们认为当前episode是值得学习的经验， 比如这条episode中，对于观测o1, agent当时采用了a1，那么我们就认为a1是好的动作——因为总reward值高。 那么我们就把网络往这个方向训练——当网络输入o1的时候，输出尽可能逼近a1。）
5. 重复步骤1， 直到结果满意为止（总的reward连创新高）

我们把 丢弃的70%的回合的reward最大值， 称为界。 每次都根据这个界，筛选出30%超过该界的回合作为学习经验 （总reward大于这个界的回合留下， 小于的删去）。 随着循环， 界的值必然逐渐上升（因为每次固定筛除70%，而随着agent的训练， 总体的reward值肯定一直提升）， 也就对应着reward逐渐上升了。 虽然这个方法很简单， 但他可以有效处理许多环境， 且容易实现。 接下来就是将该方法实现，用于解决CartPole问题了（第二章中曾一度介绍过，但没有给出解决方法）。

交叉熵法实践：玩CartPole小游戏

代码详见 Chapter04/01_cartpole.py文件， 可以从上面的github库中clone。 接下来的实践中，我们只使用了一个单层的简单神经网络，由128个神经元和Relu激活函数组成。 大部分的超参数都是默认或随机给出的。本例中可以看出， 交叉熵法很强的鲁棒性（基本不需要超参数调参）和收敛性。

CartPole小游戏在第二章中介绍过， 是Gym自带的一个环境， 其机制是玩家控制下方的木块左右移动， 防止木块上的木棍倾倒。

可以看到， 代码只有100行左右， 除去空白及import等语句，实际语句其实只需要50行不到，就能实现这个方法。

HIDDEN_SIZE = 128
BATCH_SIZE = 16
PERCENTILE = 70

一些参数的设置， 128是神经元的个数， 16是Batch的大小（每次迭代中所用到的训练样本的个数）， 70就是70%的筛选比例。

class Net(nn.Module):
    def __init__(self, obs_size, hidden_size, n_actions):
        super(Net, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(obs_size, hidden_size),
            nn.ReLU(),
            nn.Linear(hidden_size, n_actions)
        )

    def forward(self, x):
        return self.net(x)

就下来就是用第三章中介绍的Pytorch框架中的Module类，自定义了自己的网络层。 不熟悉的读者可以参考第三章， 这是最基本的Sequential搭建网络的用法。 重写forward()方法后， 我们已搭建了一个一层线性神经网络+Relu激活函数的网络。

这里需要重点注意的一点是： 我们居然没有用softmax来激活输出。 如之前提到的，我们希望网络的输出是对各个action的概率分布——即总和1的一个浮点数张量。 而在深度学习中，softmax是用来将输出激活为满足这一类型的函数——而我们现在的输出直接是线性层的输出结果， 并不能满足这一条件。 这是因为： 我们接下来要使用的nn.CrossEntropyLoss这个损失函数，会自动地对输入做softmax， 再进行交叉熵计算。 （和nn.BCEloss不同）因此，就不需要你自己再专门做一个softmax。这样做的话方便了很多，缺点就在于当你在测试的时候，要记得对神经网络的输出结果做一个softmax操作。

from collections import namedtuple
Episode = namedtuple('Episode', field_names=['reward', 'steps'])
EpisodeStep = namedtuple('EpisodeStep', field_names=['observation', 'action'])

这一步是使用了python自带库collections中的namedtuple类型。 我们都知道tuple（元组）是python的基本数据类型， 但其缺点是，每一个元素无法单独命名， 而namedtuple则可以对每个元素及元组进行命名。这个的好处后面会体现， namedtuple的用法可以参考namedtuple的用法，简单来说就是这样：

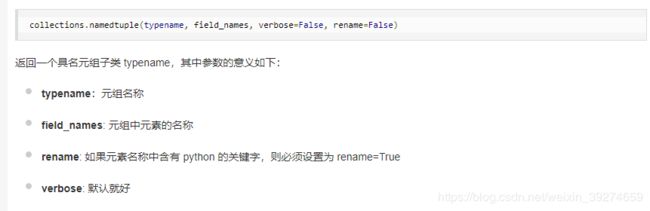
那么这段代码就是命名了两个元组：

• EpisodeStep： 用于记录回合中每一单步的结果——保存了包括观测，agent采取的动作。这也会作为训练数据。
• Episode：代表一个完整的的episode。其字段分别是总奖励值和回合中记录的EpisodeStep值。
  结合后续代码更容易理解。

def iterate_batches(env, net, batch_size):
    batch = []
    episode_reward = 0.0
    episode_steps = []
    obs = env.reset()
    sm = nn.Softmax(dim=1)
    while True:
        obs_v = torch.FloatTensor([obs])
        act_probs_v = sm(net(obs_v))
        act_probs = act_probs_v.data.numpy()[0]
        action = np.random.choice(len(act_probs), p=act_probs)
        next_obs, reward, is_done, _ = env.step(action)
        episode_reward += reward
        episode_steps.append(EpisodeStep(observation=obs, action=action))
        if is_done:
            batch.append(Episode(reward=episode_reward, steps=episode_steps))
            episode_reward = 0.0
            episode_steps = []
            next_obs = env.reset()
            if len(batch) == batch_size:
                yield batch
                batch = []
        obs = next_obs

这一段代码， 负责产生训练样本集(batch)。 首先， 将batch, episode_reward, episode_steps, obs等初始化。

• 这里注意： 我们刚刚提到，我们的神经网络里省略了softmax这一步， 因此，这里我们先使用sm = nn.Softmax(dim=1)， 然后act_probs_v = sm(net(obs_v))即表示， 对网络的输出进行softmax操作——这样，sm(net(obs_v))就是一个和为1的张量， 代表了策略——选取每个动作的概率。
• action = np.random.choice(len(act_probs), p=act_probs)，这一步就是numpy中随机类的采样方法。 这里需要注意的是：我们可以使用env.action_space查看动作空间， 在CartPole例子中，动作空间就是0和1， 分别代表向左或向右——因此，我们的动作结果， 就是在[0,1]中， 按概率（由神经网络计算得到）选取。np.random.choice(len(act_probs), p=act_probs)指的就是在range(len(act_probs)中， 按概率分布为act_probs进行选取。
• 由于后面需要torch库进行自动的梯度计算，因此我们在把样本输入网络前， 必须先转换成torch.Tensor类。
• episode_steps.append(EpisodeStep(observation=obs, action=action))，每进行一步， 将该步的观测和动作记录到命名元组中保存。
• if is_done: batch.append(Episode(reward=episode_reward, steps=episode_steps)当回合结束时，将记录了本回合每一步数据的列表episode_steps及总的reward值，保存为Episode元组， 并加入到代表最终虚训练数据的batch列表中。
• 同样，也是使用了 while True循环 + yield关键词的方式， 让每次调用本函数时，都返回一组训练样本。

def filter_batch(batch, percentile):
    rewards = list(map(lambda s: s.reward, batch))
    reward_bound = np.percentile(rewards, percentile)
    reward_mean = float(np.mean(rewards))

    train_obs = []
    train_act = []
    for example in batch:
        if example.reward < reward_bound:
            continue
        train_obs.extend(map(lambda step: step.observation, example.steps))
        train_act.extend(map(lambda step: step.action, example.steps))

    train_obs_v = torch.FloatTensor(train_obs)
    train_act_v = torch.LongTensor(train_act)
    return train_obs_v, train_act_v, reward_bound, reward_mean

上面这段代码，则是负责筛去70%的样本， 留下最好的30%的样本回合。
rewards = list(map(lambda s: s.reward, batch))，使用了map函数 —— 可以理解为对batch的每个元素都进行lambda funciton操作，等价于rewards = [func(x) for x in batch], 其中， func=lambda s: s.reward。接下来， 使用numpy库的API np.percentile(rewards, percentile)， 可以返回第一个参数中， 第70%（第二个参数）百分位的数 （从小到大排列）。也就是说，大于 reward_bound的占30%。因此，后面对每一个batch进行循环， reward值小于该阈值reward_bound的，不加入到样本中， 也就是说样本集最后留下的是奖励总额为前30%的回合经验。 train_obs , train_act分别保存每个合格样本（前30%）的观测与动作，这里使用了list的extend方法，这个方法类似于 列表的“+”操作。 即
train_obs.extend(map(lambda step: step.observation, example.steps))等价于train_obs + map(lambda step: step.observation, example.steps)。总之，通过extend方法， 样本数据被记录到了两个列表中。
再将两个列表转换为torch的Tensor类——obs是浮点，而action是整数值。 注意，转换后的张量， 第一维是样本的数量， 其余维则是每个样本的维度。 最后，返回需要的值。

最后是运行的主函数代码

if __name__ == "__main__":
    env = gym.make("CartPole-v0")
    # env = gym.wrappers.Monitor(env, directory="mon", force=True)
    obs_size = env.observation_space.shape[0]
    n_actions = env.action_space.n

    net = Net(obs_size, HIDDEN_SIZE, n_actions)
    objective = nn.CrossEntropyLoss()
    optimizer = optim.Adam(params=net.parameters(), lr=0.01)
    writer = SummaryWriter(comment="-cartpole")

    for iter_no, batch in enumerate(iterate_batches(env, net, BATCH_SIZE)):
        obs_v, acts_v, reward_b, reward_m = filter_batch(batch, PERCENTILE)
        optimizer.zero_grad()
        action_scores_v = net(obs_v)
        loss_v = objective(action_scores_v, acts_v)
        loss_v.backward()
        optimizer.step()
        print("%d: loss=%.3f, reward_mean=%.1f, reward_bound=%.1f" % (
            iter_no, loss_v.item(), reward_m, reward_b))
        writer.add_scalar("loss", loss_v.item(), iter_no)
        writer.add_scalar("reward_bound", reward_b, iter_no)
        writer.add_scalar("reward_mean", reward_m, iter_no)
        if reward_m > 199:
            print("Solved!")
            break
    writer.close()

框架与上一章最后的Demo几乎一致：

• 初始化 网络， 优化器， 损失函数， Writer（用于Tensorboard监控）
• 进行循环， 每次循环调用样本生成函数， 得到一批训练样本
• 清零梯度， 计算损失函数， 然后调用损失值的backward()方法计算梯度， 调用优化器的step()方法优化网络。
• 打印中间值， 保存Writer

运行结果如下：

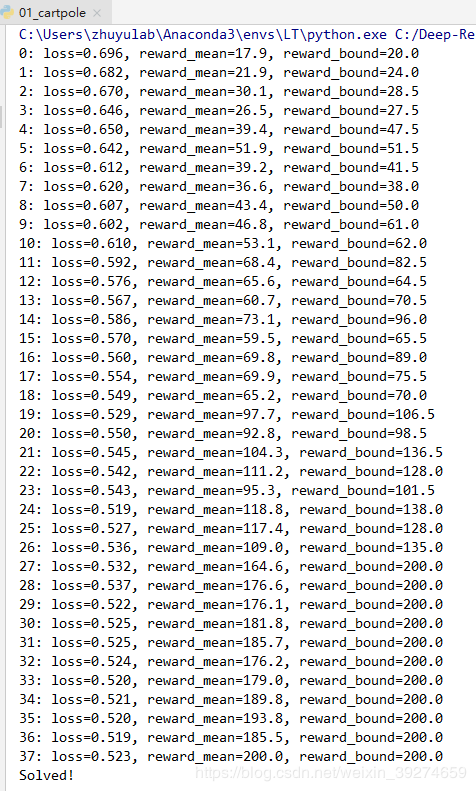
在短短30次不到的迭代中， 交叉熵方法便成功训练出了能达到200 reward的Agent——要知道我们的随机Agent的reward不到20。可见，交叉熵方法在这一问题中，是非常简便实用的。 下图是tensorboard展示的训练过程——损失值逐次下降，伴随着reward逐渐提升。

接下来，让我们暂停一会，并思考交叉熵方法，为什么可以有效工作——我们的神经网络在没有得到任何环境描述的情况， 学会了如何去更好地做出动作 —— 我们的方法并不依赖于环境的细节。这就是强化学习的迷人之处。

交叉熵的理论背景

交叉熵具体是怎么工作的？ 这一点，我觉得原书中讲的不好， 我仔细查阅了引用文献及相关资料后， 以自己的理解写一下。

这一节是介绍交叉熵的数学机理——当然，读者也可以选择读交叉熵的原论文。

对于初学者， 推荐这篇知乎的文章， 简单地了解下 交叉熵的基本概念：
传送门

我就从经典的KL散度讲起， 对于两个概率分布$p(x)$和$q(x)$ , KL散度是经典的刻画两者差距的度量标准。 首先说下什么是概率分布？

• 比如分类问题中， 总共有三种类别。 对于一个样本， 如果我们的标签知道这属于第一类别， 那么它的真实概率分布$p(x)$就可以表示为：[1, 0, 0]。即属于第一类的概率1，其余为0 。而我们预测的概率分布值$q(x)$， 就可能是 [0.7, 0.2, 0.1]， 代表$x_1$（第一类）的概率是0.7，$x_2$是0.2， $x_1$是0.1。
• 就我们当前这个例子而言， 我们的强化学习 策略——就是一种概率分布, 即$\pi (a|s)=[p_1,p_2,...p_n]$， 对应于选取动作1到动作n的概率。

简而言之， 所谓概率分布，就是指对一随机变量的分布情况描述(比如上面列举的离散情况， 概率分布就是指随机变量属于各个类的概率）。这个定义也很容易拓展到连续的情况。

那么，什么是KL散度呢？
$$D_{KL}(p\Vert q)=\sum _{i=1}^{n}p\left(x_i\right)\log \left(\frac{p\left(x_i\right)}{q\left(x_i\right)}\right)$$

上式就是KL散度的公式。 他的特点在于——当且仅当$p(x)=q(x)$时， $D_{KL}(p\Vert q)$达到最小值， 即两个概率分布的距离为0， 对应两个分布完全一致。 而两者差异越大， 则KL散度越大。

上式可以进一步改写：

$$\begin{array}{rl}{D}_{KL}(p\Vert q)& =\sum _{i=1}^{n}p\left(x_i\right)\log \left(p\left(x_i\right)\right)-\sum _{i=1}^{n}p\left(x_i\right)\log \left(q\left(x_i\right)\right)\\ & =-H(p(x))+\left[-\sum _{i=1}^{n}p\left(x_i\right)\log \left(q\left(x_i\right)\right]\right]\end{array}$$

注意， 右边等式的第一项，就是$p(x)$的熵， 是一个常数（我们算法一般是对$q$进行优化， p(x)一般认为是标签，是常量），所以，我们其实只需最小化第二项：

$$H(p,q)=-\sum _{i=1}^{n}p\left(x_i\right)\log \left(q\left(x_i\right)\right)$$

而这个$H(p,q)$， 就是被定义的 交叉熵。 由这个推导可以看出， 交叉熵是刻画两个量 $p$ 和 $q$之间的差距的， 交叉熵越小， 代表差距越小 —— 这一点和著名的MSE函数是一致的：$\mathrm{M}\mathrm{S}\mathrm{E}=(p-q{)}^2$。

知乎上有篇答案， 很好地从数学角度解释了最小化交叉熵本质上就是最大似然估计法，写的很好，大家可以参考 传送门。

知道了交叉熵的基本概念和物理含义， 就不难理解为什么将其作为神经网络的损失函数了。 比如图像分类问题（假设有四类）， 对于一个样本属于第一类， 真实的标签就是[1, 0, 0, 0]， 按上式计算交叉熵并优化网络尽可能减小它， 那么会使得神经网络最后的输出结果也尽可能地接近标签——比如[0.9, 0.1, 0.05, 0.05]这样， 就代表属于第一类的概率极高。 这个其实很像用MSE损失函数训练， 但是在深度学习中，交叉熵在许多场景下的表现更好。

那么就很容易理解， 交叉熵在强化学习这个例子中的原理了——

• 首先， 我们通过运行环境， 积累了许多经验， 并挑出前30%的经验， 以这30%经验中所采用的策略（本质是动作选择的概率分布）作为标签。
• 我们以交叉熵作为损失函数， 就能使我们网络输出的策略结果，往更趋近于这30%较优策略的方向优化——因为网络训练会降低损失值， 而和标签策略的交叉熵越小，代表和标签策略越接近， 这就可以理解为 从过往成功的经验中学习。
• 随着不断的迭代训练，网络一次次地向顶尖30%的策略学习， 这也会使得下一次产生样本集合时， 所有100%的经验的平均水平都提升了（每条经验都是基于优化的Agent产生的），也就是说， 挑出的30%的经验也在逐步越来越好（因为平均水平和上限都提升了）。经过足够的训练， 网络就逐渐往最好的性能收敛了。

总结

这一章，讲述了交叉熵法在强化学习中的应用。 在我看来， 其实就是以优秀的经验策略为标签， 让网络逐步优化。 接下来的章节中， 我们会介绍更多，更复杂也更强大的强化学习方法。