操作系统实验——磁盘调度算法（FIFS SSTF SCAN）

操作系统实验——磁盘调度算法（FIFS SSTF SCAN）

一、实验目的

1、了解磁盘调度的策略和原理；
2、理解和掌握磁盘调度算法——先来先服务算法（FCFS）、最短寻道时间优先算法（SSTF）、电梯扫描算法（SCAN）。

二、实验内容

1、模拟先来先服务法（First-Come, First-Served，FCFS），最短寻道时间优先法（Shortest Seek Time First， SSTF），电梯扫描算法（SCAN）三种磁盘调度算法；
2、对三种算法进行对比分析。
3、输入为一组请求访问磁道序列，输出为每种调度算法的磁头移动轨迹和移动的总磁道数。

三、实验原理

1、先来先服务算法（FCFS）:

按先来后到次序服务，未作优化。最简单的移臂调度算法是“先来先服务”调度算法，这个算法实际上不考虑访问者要求访问的物理位置，而只是考虑访问者提出访问请求的先后次序。 采用先来先服务算法决定等待访问者执行输入输出操作的次序时，移动臂来回地移动。先来先服务算法花费的寻找时间较长，所以执行输入输出操作的总时间也很长。

2、最短寻道时间优先算法（SSTF） :

最短寻找时间优先调度算法总是从等待访问者中挑选寻找时间最短的那个请求先执行的，而不管访问者到来的先后次序。与先来先服务、算法比较，大幅度地减少了寻找时间，因而缩短了为各访问者请求服务的平均时间，也就提高了系统效率。但最短查找时间优先（SSTF）调度，FCFS会引起读写头在盘面上的大范围移动，SSTF查找距离磁头最短（也就是查找时间最短）的请求作为下一次服务的对象。SSTF查找模式有高度局部化的倾向，会推迟一些请求的服务，甚至引起无限拖延（又称饥饿）。

3、扫描算法（SCAN）：

SCAN 算法又称电梯调度算法。SCAN算法是磁头前进方向上的最短查找时间优先算法，它排除了磁头在盘面局部位置上的往复移动，SCAN算法在很大程度上消除了SSTF算法的不公平性，但仍有利于对中间磁道的请求。“电梯调度”算法是从移动臂当前位置开始沿着臂的移动方向去选择离当前移动臂最近的那个柱访问者，如果沿臂的移动方向无请求访问时，就改变臂的移动方向再选择。但是，“电梯调度”算法在实现时，不仅要记住读写磁头的当前位置，还必须记住移动臂的当前前进方向。

四、实验中用到的系统调用函数

  实验只是模拟实现磁盘调度功能，不需要系统调用函数。

五、实验要求

1、输入为一组请求访问磁道序列，该序列和所选磁道个数要求随机生成，输出为每种调度算法的磁头移动轨迹和移动的总磁道数；

srand((int)time(NULL));
	cout << "请输入生成的访问磁道进程数量：";
	int n, m, p=0;
	int flag ;
	string direction;
	cin >> n;
	int a[100];
	for (int i = 0; i < n; i++)
	{
		a[i] = rand() % 1000;
	}cout << "生成的访问进程为：";
	for (int i = 0; i < n; i++)
	{
		if (i % 5 == 0)
		{
			cout << endl;
		}
		cout << a[i] << "  ";

	}

2、输入磁道范围 0~1000 ，输入所选磁道个数0~1000；

3、画出主程序流程图；

源代码：

include <iostream>
#include
#include 

using namespace std;
class DISK
{
private:
	int Movedistance;//移动距离	
	int Lable[100];//标号指针
	string Movedirection;//移动方向
public:
	int  Calculate_Diference(int a, int b)//计算移动距离（差值的绝对值）
	{
		return (a - b > 0 ? a - b : b - a);
	}
	void ShowPath(int a[], int x, int len)//调度过程  时间复杂度O(n)
	{
		cout << "从" << x << "号磁道开始" << endl;
		for (int i = 1; i < len + 1; i++)
		{
			cout << "下一个访问的磁道号：" << a[i] << "\t移动的距离：" << Calculate_Diference(a[i], a[i - 1]) << endl;
		}
	}
	void CalculateMoveDistance(int a[], int x, int len)//计算平均寻道长度  时间复杂度O(n)
	{
		double count = 0;;
		double average = 0;
		for (int i = 1; i < len + 1; i++)
		{
			count += Calculate_Diference(a[i], a[i - 1]);
		}
		average = count / len;
		cout << "平均寻道长度为：" << average << endl;
	}
	void FIFS(int a[], int x, int len)//先来先服务算法  
	{
		Lable[0] = x;//数组中第一个数为当前磁道位置
		for (int i = 0; i < len; i++)
		{
			Lable[i + 1] = a[i];
		}
		ShowPath(Lable, x, len);
		CalculateMoveDistance(Lable, x, len);
	}
	void SSTF(int a[], int x, int len)//最短寻道时间优先
	{
		Lable[0] = x;//数组中第一个数为当前磁道位置
		int m = 0;
		int temp = 0;
		for (int i = 0; i < len; i++)//该循环为了找出访问顺序，Lalbe[];
		{
			m = i;
			for (int j = i; j < len; j++)//遍历数组a[]，找出与当前磁头最近的一个磁道。
			{
				if (Calculate_Diference(a[j + 1], Lable[i]) < Calculate_Diference(a[m], Lable[i]))
				{
					m = j + 1;
					temp = a[j + 1];
				}
				else temp = a[m];
			}
			Lable[i + 1] = temp;
			int temp2 = a[m];//找出该磁道后将找到的数据置换到数组最前面，以便下一次遍历时跳过；
			a[m] = a[i];
			a[i] = temp2;
		}
		ShowPath(Lable, x, len);
		CalculateMoveDistance(Lable, x, len);
	}

	void insertsort(int a[], int len)//插入排序
	{
		int temp;
		for (int i = 1; i < len; i++)
		{
			temp = a[i];
			int j = i - 1;
			while (j >= 0 && a[j] > temp)
			{
				a[j + 1] = a[j];
				j--;
			}
			a[j + 1] = temp;
		}
	}

	void SCAN(int a[], int x, int len,string  Movedirection)//扫描算法
	{
		Lable[0] = x;//数组中第一个数为当前磁道位置
		int m = 0, r = 0, l = 0, r2 = 0, l2 = 0;
		int temp = 0;
		int right[100];
		int rightelse[100];
		int left[100];
		int leftelse[100];
		for (int i = 0; i < len; i++)//磁头向磁道增大的方向移动时，将大的磁道组成一个数组，其他的磁道组成一个数组
		{
			if (Lable[0] < a[i])
			{
				right[r] = a[i];
				r++;
			}
			else rightelse[r2] = a[i], r2++;
		}
		for (int i = 0; i < len; i++)//磁头向磁道减小的方向移动时，将小的磁道组成一个数组，其他的磁道组成一个数组
		{
			if (Lable[0] > a[i])
			{
				left[l] = a[i];
				l++;
			}
			else leftelse[l2] = a[i], l2++;
		}
		if (Movedirection == "right")
		{
			insertsort(right, r);//将大的进行排序
			for (int j = 0; j < r; j++)
			{
				Lable[j + 1] = right[j];
			}
			for (int i = 0; i < r2; i++)//找剩余的
			{
				m = i;
				for (int j = i; j < r2; j++)//遍历数组a[]，找出与当前磁头最近的一个磁道。
				{
					if (Calculate_Diference(rightelse[j + 1], Lable[i]) < Calculate_Diference(rightelse[m], Lable[i]))
					{
						m = j + 1;
						temp = rightelse[j + 1];
					}
					else temp = rightelse[m];
				}
				Lable[i +r+ 1] = temp;
				int temp2 = rightelse[m];//找出该磁道后将找到的数据置换到数组最前面，以便下一次遍历时跳过；
				rightelse[m] = rightelse[i];
				rightelse[i] = temp2;
			}
			
		}
		if (Movedirection == "left")
		{
			int c = 1;
			insertsort(left, l);//将小的进行排序
			for (int j = l - 1; j >= 0; j--)
			{
				Lable[c] = left[j];
				c++;
			}
			for (int i = 0; i < l2; i++)//找剩余的
			{
				m = i;
				for (int j = i; j < l2; j++)//遍历数组a[]，找出与当前磁头最近的一个磁道。
				{
					if (Calculate_Diference(leftelse[j + 1], Lable[i]) < Calculate_Diference(leftelse[m], Lable[i]))
					{
						m = j + 1;
						temp = leftelse[j + 1];
					}
					else temp = leftelse[m];
				}
				Lable[i + l + 1] = temp;
				int temp2 = leftelse[m];//找出该磁道后将找到的数据置换到数组最前面，以便下一次遍历时跳过；
				leftelse[m] = leftelse[i];
				leftelse[i] = temp2;
			}
		}
		ShowPath(Lable, x, len);
		CalculateMoveDistance(Lable, x, len);
	}
};
int main()
{
	DISK disk;
	srand((int)time(NULL));
	cout << "请输入生成的访问磁道进程数量：";
	int n, m, p=0;
	int flag ;
	string direction;
	cin >> n;
	int a[100];
	for (int i = 0; i < n; i++)
	{
		a[i] = rand() % 1000;
	}
	cout << "生成的访问进程为：";
	for (int i = 0; i < n; i++)
	{
		if (i % 5 == 0)
		{
			cout << endl;
		}
		cout << a[i] << "  ";

	}
	cycle1:cout << "\n请输入起始位置(0-200)：";
	cin >> m;
	cycle2:cout << "请输入磁盘调度方式(1:FIFS   2:SSTF   3:SCAN)" << endl;
	cin >> flag;
	switch (flag)
	{
	case 1:
		cout << "执行FIFS算法" << endl; disk.FIFS(a, m, n); cout << "\n\n"; break;
	case 2:
		cout << "执行SSTF算法" << endl; disk.SSTF(a, m, n); cout << "\n\n"; break;
	case 3:
		cout << "执行SCAN" << endl;
		cout << "请确定扫描方向（向外扫描：'right',向内扫描'left')";   
		cin >> direction;
		disk.SCAN(a, m, n, direction); cout << "\n\n"; break;
	}
	cout << "\n是否继续？(1：继续    0：退出    2：重新确定初始位置";
	cin >> p;
	if (p == 1)
		goto cycle2;
	else if (p == 2)
	{
		goto cycle1;
	}
	else return 0;
}

4、截屏输出实验结果

以下结果为从100磁道号开始进行扫描时候的实验结果：

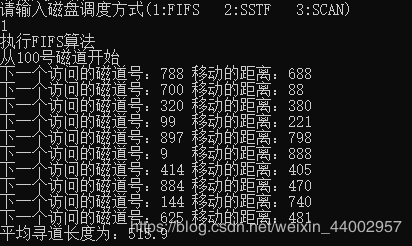
FIFO算法，时间复杂度O(n) 平寻道长度515.9

SSTF算法：时间复杂度O(n^2) 平均寻道长度106.9

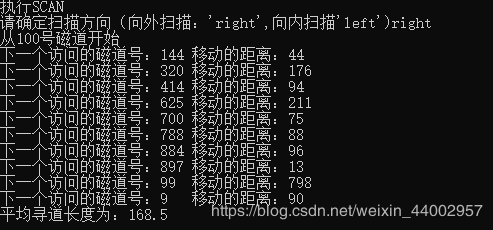
SCAN算法（向外扫描）：时间复杂度O(n^2),平均寻道长度：168.5

SCAN算法（向内扫描）：时间复杂度O(n^2),平均寻道长度：97.9

以下结果为从500磁道号开始进行扫描时候的实验结果：

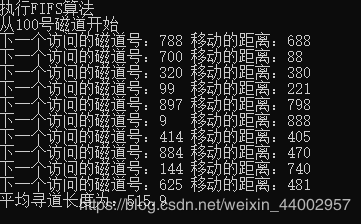
FIFS算法：时间复杂度为;O(n) 平均寻道长度为：515.9

SSFT算法：时间复杂度为;O(n^2) 平均寻道长度为：106.9

SCAN算法(向外)：时间复杂度为;O(n^2) 平均寻道长度为：168.5

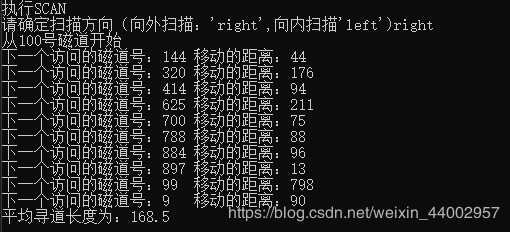
SCAN算法(向内)：时间复杂度为;O(n^2) 平均寻道长度为：97.9

5、根据实验结果与理论课讲述的原理进行实验分析。

由实验结果的截图来看，
（1）对于FIFS算法：磁道初始位置在整体数据偏小或者偏大的位置时，FIFS算法的平均寻道长度是最长的，由此可知FIFS算法 虽然时间复杂度小，但是平均寻道长度显著高于其他两个算法，对磁盘移动臂的消耗就多。
磁道初始位置在整体数据处于整体数据中间的时候，FIFS算法的平均寻道长度较短，因为时间复杂度最小，对磁盘移动臂的消耗也相对较小，所以该算法可用
（2）对于SSTF算法来说：无论磁道初始位置在整体数据的什么位置，平均寻道长度变化幅度相对不大，比较稳定，对于本次数据来讲，稳定在106到137
（3）对于SCAN算法来说，
1：磁道初始位置在整体数据的（偏大/偏小）位置时候，SCAN算法的平均寻道长的在（向外/向内）访问时两者的平均寻道长度之差较大，
处于偏小位置时：移动臂向外访问的平均训导长度较大为168.5(以100为初始),向内的为：97.9。
处于偏大位置时可以看出与处于偏小位置时的结果相反。
2：磁道初始位置在整体数据的中间位置时，SCan算法的平均寻道长度在向外和向内访问时两者的平均寻道长度之差较小，相对来说较稳定。

六、思考题

1、通过对每个算法进行时间复杂度分析对比，每个算法的效率如何？

由上述的实验结果分析来看，
（1）当磁道初始位置在整体访问磁道数据的偏大或者偏小位置的时候，FIFS时间复杂度为O(n)最低，其他两个算法时间复杂度均为O(n^2) 但是FIFS的平均寻道长度明显高于其他两个算法，弃用。
处于偏小位置的时候可以使用SCAN算法中移动臂向内访问算法和SSTF算法，这两个算法在这种情况时间复杂度相同，平均寻道长度也接近。
处于偏大位置时相反。
（2）当磁道初始位置在整体访问磁道数据的中间位置的时候，FIFS算法时间复杂度最小，平均寻道长度与其他两种算法相差不多，所以可以使用FIFS算法
对于三种算法的稳定性来看：
FIFS>SCAN>SSTF

2、若所有硬盘全部设计成电子硬盘，哪个磁盘调度算法最合适？

因为电子硬盘读取速度极快而且不涉及磁盘调度臂的问题，所以应该使用时间复杂度最低的FIFS算法，该算法时间复杂度为：O(n);