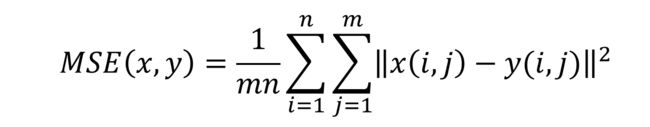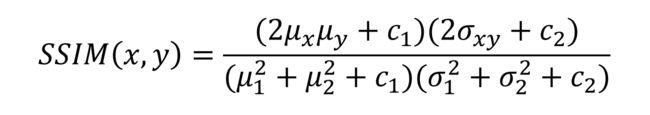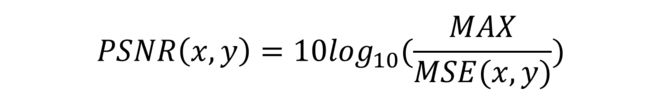图像相似度评价指标
在图像处理中我们经常遇到需要评价两张图像是否相似,给出其相似度的指标,这里总结了三种评判指标均方误差MSE, 结构相似性SSIM, 以及峰值信噪比PSNR, 分三个小结介绍其原理以及对应的matlab以及tensorflow版本的算法实现。
均方误差MSE
即m×n单色图像 I 和 K(原图像与处理图像)之间均方误差,定义为:
Matlab实现
function MSE = mse(I, K)
[M,N,D] = size(I);
Diff = double(I)-double(K);
MSE = sum(Diff(:).^2)/numel(I);
end
Tensorflow实现
# import tensorflow as tf
def MSE(I, K):
x, y = tf.cast(I, tf.float32), tf.cast(K, tf.float32)
mse = tf.losses.mean_squared_error(labels=y, predictions=x)
return mse
结构相似性SSIM
- 结构相似性:
自然图像具有极高的结构性,表现在图像的像素间存在着很强的相关性,尤其是在空间相似的情况下。这些相关性在视觉场景中携带着关于物体结构的重要信息。我们假设人类视觉系统(HSV)主要从可视区域内获取结构信息。所以通过探测结构信息是否改变来感知图像失真的近似信息。
大多数的基于误差敏感度(error sensitivity)的质量评估方法(如MSE,PSNR)使用线性变换来分解图像信号,这不会涉及到相关性。我们要讨论的SSIM就是要找到更加直接的方法来比较失真图像和参考图像的结构。- SSIM指数
物体表面的亮度信息与照度和反射系数有关,且场景中的物体的结构与照度是独立的,反射系数与物体有关。我们可以通过分离照度对物体的影响来探索一张图像中的结构信息。这里,把与物体结构相关的亮度和对比度作为图像中结构信息的定义。因为一个场景中的亮度和对比度总是在变化的,所以我们可以通过分别对局部的处理来得到更精确的结果。
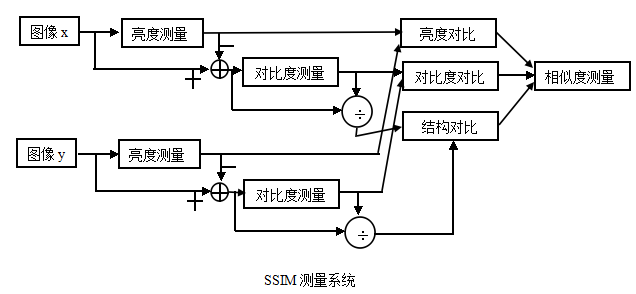
SSIM的算法流程图原理图如下所示:
SSIM的求解公式如下:
其中u_x是x的平均值,u_y是y的平均值,σ_x是x的方差,σ_y是y的方差,σ_{xy}是x和y的协方差。c_1=(k_1*L)^2,c_2=(k_2*L)^2是用来维持稳定的常数。L是像素值的动态范围。k_1=0.01,k_2=0.03。
结构相似性的范围为-1到+1(即SSIM∈(-1, 0])。当两张图像一模一样时,SSIM的值等于1。
Matlab实现
function [mssim, ssim_map,siga_sq,sigb_sq] = SSIM(ima, imb)
% ========================================================================
%ssim的算法主要参考如下论文:
%Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, "Image
% quality assessment: From error visibility to structural similarity,"
% IEEE Transactios on Image Processing, vol. 13, no. 4, pp. 600-612,
% Apr. 2004.
% 首先对图像加窗处理,w=fspecial('gaussian', 11, 1.5);
% (2*ua*ub+C1)*(2*sigmaa*sigmab+C2)
% SSIM(A,B)=——————————————————————————————————————————————————
% (ua*ua+ub*ub+C1)(sigmaa*sigmaa+sigmab*sigmab+C2)
% C1=(K1*L);
% C2=(K2*L); K1=0.01,K2=0.03
% L为灰度级数,L=255
%-------------------------------------------------------------------
% ima - 比较图像A
% imb - 比较图像B
%
% ssim_map - 各加窗后得到的SSIM(A,B|w)组成的映射矩阵
% mssim - 对加窗得到的SSIM(A,B|w)求平均,即最终的SSIM(A,B)
% siga_sq - 图像A各窗口内灰度值的方差
% sigb_sq - 图像B各窗口内灰度值的方差
%-------------------------------------------------------------------
% Cool_ben
%=======================================================================
w = fspecial('gaussian', 11, 1.5); %window 加窗
K(1) = 0.01;
K(2) = 0.03;
L = 255;
ima = double(ima);
imb = double(imb);
C1 = (K(1)*L)^2;
C2 = (K(2)*L)^2;
w = w/sum(sum(w));
ua = filter2(w, ima, 'valid');%对窗口内并没有进行平均处理,而是与高斯卷积,
ub = filter2(w, imb, 'valid'); % 类似加权平均
ua_sq = ua.*ua;
ub_sq = ub.*ub;
ua_ub = ua.*ub;
siga_sq = filter2(w, ima.*ima, 'valid') - ua_sq;
sigb_sq = filter2(w, imb.*imb, 'valid') - ub_sq;
sigab = filter2(w, ima.*imb, 'valid') - ua_ub;
ssim_map = ((2*ua_ub + C1).*(2*sigab + C2))./((ua_sq + ub_sq + C1).*(siga_sq + sigb_sq + C2));
mssim = mean2(ssim_map);
end
Tensorflow实现
# import tensorflow as tf
def _tf_fspecial_gauss(size, sigma):
"""Function to mimic the 'fspecial' gaussian MATLAB function"""
x_data, y_data = np.mgrid[-size//2 + 1:size//2 + 1, -size//2 + 1:size//2 + 1]
x_data = np.expand_dims(x_data, axis=-1)
x_data = np.expand_dims(x_data, axis=-1)
y_data = np.expand_dims(y_data, axis=-1)
y_data = np.expand_dims(y_data, axis=-1)
x = tf.constant(x_data, dtype=tf.float32)
y = tf.constant(y_data, dtype=tf.float32)
g = tf.exp(-((x**2 + y**2)/(2.0*sigma**2)))
return g / tf.reduce_sum(g)
def tf_ssim(img1, img2, cs_map=False, mean_metric=True, size=11, sigma=1.5):
window = _tf_fspecial_gauss(size, sigma) # window shape [size, size]
K1 = 0.01
K2 = 0.03
L = 1 # depth of image (255 in case the image has a different scale)
C1 = (K1*L)**2
C2 = (K2*L)**2
mu1 = tf.nn.conv2d(img1, window, strides=[1, 1, 1, 1], padding='VALID')
mu2 = tf.nn.conv2d(img2, window, strides=[1, 1, 1, 1], padding='VALID')
mu1_sq = mu1*mu1
mu2_sq = mu2*mu2
mu1_mu2 = mu1*mu2
sigma1_sq = tf.nn.conv2d(img1*img1, window, strides=[1, 1, 1, 1], padding='VALID') - mu1_sq
sigma2_sq = tf.nn.conv2d(img2*img2, window, strides=[1, 1, 1, 1], padding='VALID') - mu2_sq
sigma12 = tf.nn.conv2d(img1*img2, window, strides=[1, 1, 1, 1], padding='VALID') - mu1_mu2
if cs_map:
value = (((2*mu1_mu2 + C1)*(2*sigma12 + C2))/((mu1_sq + mu2_sq + C1) *
(sigma1_sq + sigma2_sq + C2)),
(2.0*sigma12 + C2)/(sigma1_sq + sigma2_sq + C2))
else:
value = ((2*mu1_mu2 + C1)*(2*sigma12 + C2))/((mu1_sq + mu2_sq + C1) *
(sigma1_sq + sigma2_sq + C2))
if mean_metric:
value = tf.reduce_mean(value)
return value
def tf_ms_ssim(img1, img2, mean_metric=True, level=5):
weight = tf.constant([0.0448, 0.2856, 0.3001, 0.2363, 0.1333], dtype=tf.float32)
mssim = []
mcs = []
for l in range(level):
ssim_map, cs_map = tf_ssim(img1, img2, cs_map=True, mean_metric=False)
mssim.append(tf.reduce_mean(ssim_map))
mcs.append(tf.reduce_mean(cs_map))
filtered_im1 = tf.nn.avg_pool(img1, [1, 2, 2, 1], [1, 2, 2, 1], padding='SAME')
filtered_im2 = tf.nn.avg_pool(img2, [1, 2, 2, 1], [1, 2, 2, 1], padding='SAME')
img1 = filtered_im1
img2 = filtered_im2
# list to tensor of dim D+1
mssim = tf.stack(mssim, axis=0)
mcs = tf.stack(mcs, axis=0)
value = (tf.reduce_prod(mcs[0:level-1]**weight[0:level-1])*(mssim[level-1]**weight[level-1]))
if mean_metric:
value = tf.reduce_mean(value)
return value
或者,emm,Tensorflow r1.8考虑使用下面函数:
tf.image.ssim(
img1,
img2,
max_val
)
具体使用方式参考:传送门
峰值信噪比PSNR
PSNR本质上与MSE相同,是MSE的对数表示。
峰值信噪比PSNR衡量图像失真或是噪声水平的客观标准。2个图像之间PSNR值越大,则越相似。普遍基准为30dB,30dB以下的图像劣化较为明显。定义为:
Matlab实现
function [PSNR, MSE]=psnr(I,K)
[M,N,D] = size(I);
Diff = double(I)-double(K);
MSE = sum(Diff(:).^2)/numel(I);
PSNR=10*log10(255^2/MSE);
end
Tensorflow实现
# import tensorflow as tf
def PSNR(I, K):
x, y = tf.cast(I, tf.float32), tf.cast(K, tf.float32)
mse = tf.losses.mean_squared_error(labels=y, predictions=x)
psnr = 10*tf.log(255**2/mse)/tf.log(10)
return psnr
-
↩经有情人士质疑SSIM的取负值情况不存在,考虑使用matlab进行下面的代码测#试:
[1]: >matlab [^_^]: >A(:,:) = round(255*rand(100,100)); [^_^]: >B(:,:) = abs(255 - A(:,:)); [^_^]: >[mssim, ssimmap, siga_sq,sigb_sq] = ssim(A, B); [^_^]: >