Gaussian function学习

参考自维基百科：

在数学上，高斯函数的形式为

对于任意实数常量$a,b,c(c̸=0)$。高斯函数的曲线为一个钟型曲线。参数$a$为曲线波峰的高度，$b$为波峰的中心的位置，$c$为标准差，控制着曲线宽度。
高斯函数经常被用于表示一个正态分布随机变量的概率密度函数，其中期望值$\mu =b$且方差${\sigma }^2=c$，这种情况下，高斯的形式为：

高斯函数被广泛应用于统计学中来描述正态分布，在信号处理领域定义为高斯滤波，在图像处理领域二维高斯函数用于高斯模糊，在数学中用于解决热传导方程和扩散方程，并定义了Weierstrass transform。

一维高斯函数：

二维高斯函数：

其中$A$为振幅，$x_0,y_0$为高斯的中心，${\sigma }_x,{\sigma }_y$为x，y方向的扩展范围，如图所示为$A=1,x_0=y_0=0,{\sigma }_x={\sigma }_y=1$
通常，一个二维的椭圆高斯函数可以表示为：

其中矩阵是正定的，在这里，上述图片中高斯的参数为$A=1,(x_0,y_0)=(0,0),a=c=1/2,b=0$。
将$a,b,c$分别表示为：

因此我们可以以顺时针角度$\theta$旋转高斯函数（对于逆时针旋转只需要将$b$取反），例如：
$\theta =0$时

$\theta =\pi /6$时

$\theta =\pi /3$时

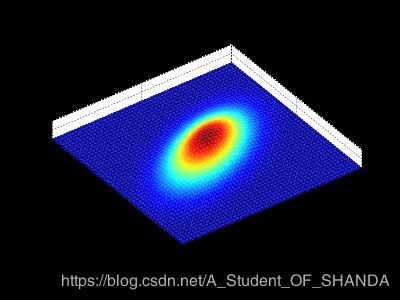
多维高斯函数：

在n维空间中高斯函数被定义为：

其中是一个n维列向量，A是一个正定的nxn矩阵，T表示矩阵转置。

参考自 http://cs229.stanford.edu/section/gaussians.pdf

这篇文章里详细介绍了多元高斯函数的形式即推导过程，很详细。
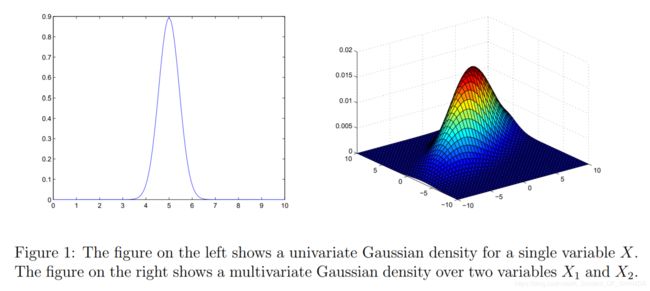
给定随机变量$X=[X_1,...,X_n{]}^T$，服从多元正态分布或者称之为多元高斯分布，其中，$\mu \in R^n$，协方差矩阵为$\Sigma$，概率密度函数为：

一元高斯

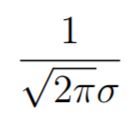是一个常量，可以理解为是有个归一化因子，用于保证：

而多元情况下，有：

协方差矩阵

协方差矩阵在统计学和机器学习中随处可见，一般而言，可视作方差和协方差两部分组成，即方差构成了对角线上的元素，协方差构成了非对角线上的元素。

对于两个随机变量X和Y，它们的协方差定义为：

协方差矩阵表示为$\Sigma$，是一个$n\times n$的矩阵，矩阵的$(i,j)$项为$Cov[X_i,X_j]$。

多元高斯函数

二维高斯函数，协方差矩阵是对角矩阵：

在这种情况下，高斯函数表示为：


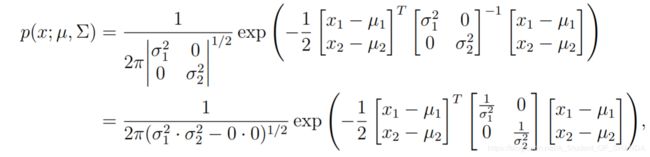
可以看到，二元高斯函数可以表示为两个独立的的高斯函数的乘积。一般而言，n维高斯函数，其中均值$\mu \in R^n$，对角协方差矩阵为$\Sigma =diag({\sigma }_1^2,{\sigma }_2^2,...,{\sigma }_n^2)$是由n个独立的高斯函数组成的。