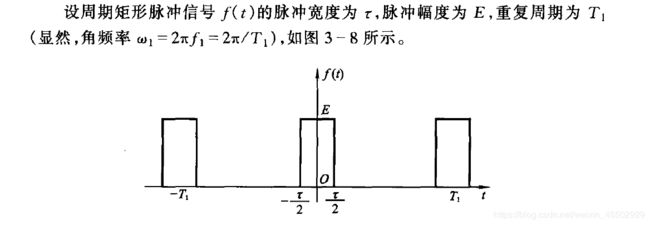
信号与系统 Part 2：傅里叶级数和傅里叶变换(1) 典型周期信号的傅里叶级数推导

配郑君里《信号与系统》第三版 3.3

0. 傅里叶级数展开公式

其他有关傅里叶级数的总结可见博文
$$f(t)=\frac{1}{2}{a}_0+\sum _{n=1}^{\infty }\left[a_n\cos (n{\omega }_{1}t)+b_n\sin (n{\omega }_{1}t)\right]$$

$a_0$前的系数只是为了保持与其他$a_i$表达式的一致

其中，
$$\begin{gathered} a_n=\frac{2}{T_1}{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}f(t)\cos (n{\omega }_{1}t)\mathrm{d}t,n=0,1,2\cdots \\ {b}_n=\frac{2}{T_1}{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}f(t)\sin (n{\omega }_{1}t)\mathrm{d}t,n=1,2,3\cdots \end{gathered}$$

关于为什么$a_0$是$\frac{1}{T_1}$，而$a_n$是$\frac{2}{T_1}$。思考最初的推导过程，我们是将正交函数系和原函数相乘，得到一系列的关于系数的积分等式，$a_0$对应直流部分，常数直接积分，区间长度为$T_1$，因而除过去就是$\frac{1}{T_1}$，而相应$a_n$积分，由正交性，最终留下的是相应三角值的平方，由半角公式，给出一个$\frac{1}{2}$的常数，所以积分得到$\frac{T_1}{2}$，除过去得到$\frac{2}{T_1}$。

1. 周期矩形脉冲信号

偶函数，仅需推导$a_n$项。

$$\frac{1}{2}{a}_0=\frac{1}{T_1}{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}f(t)\mathrm{d}t=\frac{1}{T_1}{\int }_{-\frac{\tau }{2}}^{\frac{\tau }{2}}E\mathrm{d}t=\frac{E\tau }{T_1}$$
$$\begin{array}{rl}{a}_n& =\frac{2}{T_1}{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}f(t)\cos (n{\omega }_{1}t)\mathrm{d}t\\ & =\frac{2}{T_1}{\int }_{-\frac{\tau }{2}}^{\frac{\tau }{2}}f(t)\cos (n{\omega }_{1}t)\mathrm{d}t\\ & =\frac{2E}{n{\omega }_1{T}_1}\cdot 2\sin (n{\omega }_{1}t){|}_0^{\frac{\tau }{2}}=\frac{4E}{n{\omega }_1{T}_1}\sin \left(n{\omega }_1\frac{\tau }{2}\right)\end{array}$$
随后，灵活运用${\omega }_1{T}_1=2\pi$，得到：
$$a_n=\frac{2E}{n\pi }\sin \left(n\pi \frac{\tau }{T_1}\right)$$
上面这个式子可以生动地反映出频谱特性，即振幅呈调和收缩，整体为表现出振荡。

1.1. 抽样函数形式

利用抽样函数，进行改写：
$$a_n=\frac{2E}{n\pi }\frac{n\pi \tau }{T_1}\mathrm{S}\mathrm{a}\left(\frac{n\pi \tau }{T_1}\right)=\frac{2E\tau }{T_1}\mathrm{S}\mathrm{a}\left(\frac{n\pi \tau }{T_1}\right)$$
还可以转化成用${\omega }_1$表示的形式：
$$a_n=\frac{E\tau {\omega }_1}{\pi }\mathrm{S}\mathrm{a}\left(\frac{n{\omega }_1\tau }{2}\right)$$
这是一个系数非1的抽样函数，在此基础上，我们对周期脉冲的赋值特性有了更加深刻的了解，即存在一个明显的收敛趋势，通信时我们只需考虑在频带内部的部分即可。

1.2. 奇偶性分析以及对称方波

最终的展开式为：
$$f(t)=\frac{E\tau }{T_1}+\frac{2E\tau }{T_1}\sum _{n=1}^{\infty }\mathrm{S}\mathrm{a}\left(\frac{n\pi \tau }{T_1}\right)\cos \left(n{\omega }_{1}t\right)$$
这其中常数是一个偶函数才可能有的成分。分析第二部分，为一个对称脉冲。

如果我们将脉冲宽度调整为$\frac{T_1}{2}$，那么最终就会构成一个对称方波。

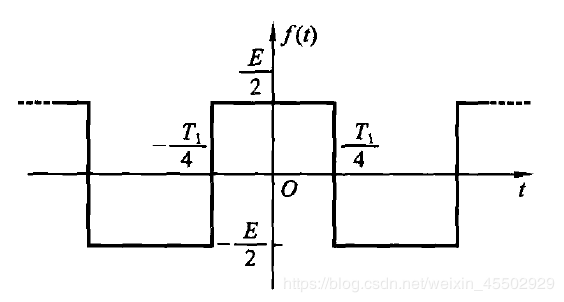
亦即
$$f(t)=\frac{2E}{\pi }\sum _{n=1}^{\infty }\frac{1}{n}\sin \left(\frac{n\pi }{2}\right)\cos \left(n{\omega }_{1}t\right)$$

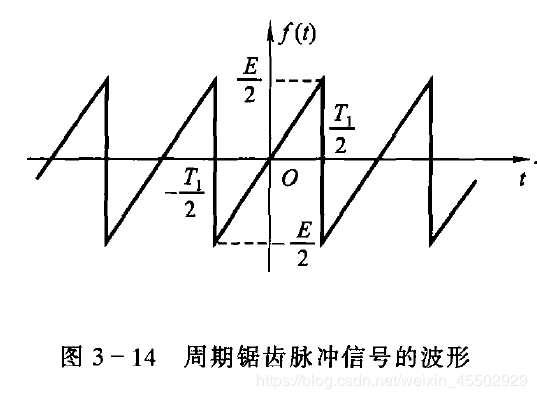
2. 周期锯齿脉冲信号

这是一个奇函数，因而展开为
$$f(t)=b_n\sin (n{\omega }_{1}t)$$
其中
$$\begin{array}{rl}{b}_n& =\frac{2}{T_1}{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}\frac{E}{T_1}t\sin (n{\omega }_{1}t)\mathrm{d}t=\frac{2E}{T_1^2}{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}t\mathrm{d}\left[\cos (n{\omega }_{1}t)\right]\\ & =\frac{2E}{T_1^2}\left(\frac{-1}{n{\omega }_1}\right)\left[2\frac{T_1}{2}(-1{)}^n-{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}\cos (n{\omega }_{1}t)\mathrm{d}t\right]\\ & =\frac{2E}{T_1^2}\left(\frac{-1}{n{\omega }_1}\right)\left[T_1(-1{)}^n-0\right]\\ & =\frac{2E}{T_{1}n{\omega }_1}(-1{)}^{(n+1)}=\frac{E}{n\pi }(-1{)}^{n+1}\end{array}$$
最终的展开式为：
$$\begin{array}{rl}f(t)& =\frac{E}{\pi }\sum _{n=1}^{\infty }(-1{)}^{n+1}\frac{1}{n}\sin (n{\omega }_{1}t)\\ & =\frac{E}{\pi }\left[\sin ({\omega }_{1}t)-\frac{1}{2}\sin (2{\omega }_{1}t)+\frac{1}{3}\sin (3{\omega }_{1}t)-\frac{1}{4}\sin (4{\omega }_{1}t)\cdots \right]\end{array}$$

3. 周期三角脉冲信号

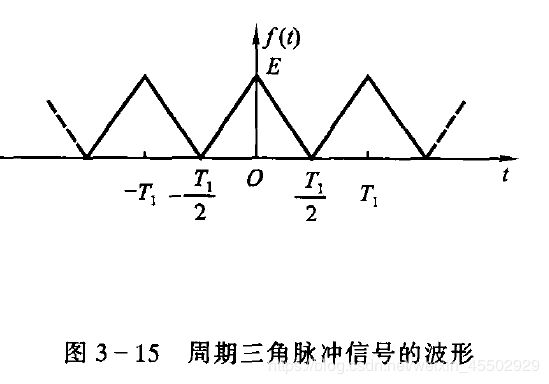
这是一个偶函数，所以我们只需展成如下形式：
$$f(t)=a_0+\sum _{n=1}^{\infty }{a}_n\sin (n{\omega }_{1}t)\mathrm{d}t$$
其中$a_0$为一个周期上的积分，易得$a_0=\frac{E}{2}$

将三角脉冲分解成一个直流信号和一个倒绝对值信号的加和，绝对值信号是偶对称信号，于是积分过程中可以有：
$$\begin{array}{rl}{a}_n& =\frac{2}{T_1}{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}f(t)\cos (n{\omega }_{1}t)\mathrm{d}t\\ & =\frac{2}{T_1}\left[{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}E+\frac{2E}{T_1}\left({\int }_{-\frac{T_1}{2}}^0-{\int }_0^{\frac{T_1}{2}}\right)t\right]\cos (n{\omega }_{1}t)\mathrm{d}t\\ & =\frac{2}{T_1}\left(0-\frac{4E}{T_1}{\int }_0^{\frac{T_1}{2}}t\right)\cos (n{\omega }_{1}t)\mathrm{d}t\\ & =-\frac{2}{T_1}\frac{4E}{T_1}\frac{1}{n{\omega }_1}\left[t\sin (n{\omega }_{1}t){|}_0^{\frac{\pi }{2}}-{\int }_0^{\frac{T_1}{2}}\sin (n{\omega }_{1}t)\mathrm{d}t\right]\\ & =-\frac{8E}{n{\omega }_1{T}_1^2}\left[0-\frac{2}{n{\omega }_1}\right]\\ & =\frac{16}{n{\omega }_1^2{T}_1^2}=\frac{16}{n(2\pi {)}^2}=\frac{4}{n{\pi }^2}\end{array}$$
最终展开式为：
$$\begin{array}{rl}f(t)& =\frac{E}{2}+\frac{4E}{{\pi }^2}\left[\cos ({\omega }_{1}t)+\frac{1}{3^2}\cos (3{\omega }_{1}t)+\frac{1}{5^2}\cos (5{\omega }_{1}t)+\cdots \right]\\ & =\frac{E}{2}+\frac{4E}{{\pi }^2}\sum _{n=1}^{\infty }\frac{1}{n^2}{\sin }^2\left(\frac{n\pi }{2}\right)\cos (n{\omega }_{1}t)\end{array}$$

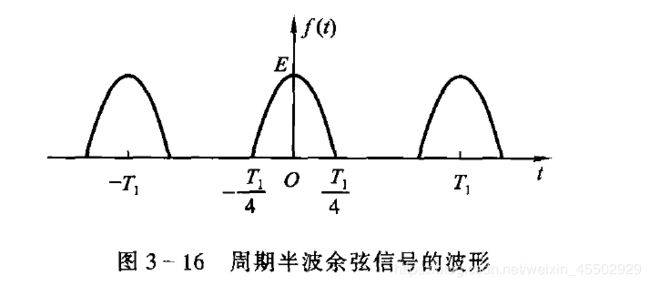
4. 周期半波余弦信号

直接写$a_n$的推导过程：
$$\frac{1}{2}{a}_0=\frac{1}{T_1}{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}f(t)\mathrm{d}t=\frac{1}{T_1}{\int }_{-\frac{T_1}{4}}^{\frac{T_1}{4}}E\cos ({\omega }_{1}t)\mathrm{d}t=\frac{1}{{\omega }_1{T}_1}2E=\frac{E}{\pi }$$
$$\begin{array}{rl}{a}_n& =\frac{2}{T_1}{\int }_{-\frac{T_1}{2}}^{\frac{T_1}{2}}f(t)\cos (n{\omega }_{1}t)\mathrm{d}t\\ & =\frac{2}{T_1}{\int }_{-\frac{T_1}{4}}^{\frac{T_1}{4}}E\cos ({\omega }_{1}t)\cos (n{\omega }_{1}t)\mathrm{d}t\\ & =\frac{2E}{T_1}{\int }_0^{\frac{T_1}{4}}\cos \left[(n+1){\omega }_{1}t\right]+\cos [(n-1){\omega }_{1}t]\mathrm{d}t\\ & =\frac{2E}{{\omega }_1{T}_1}\left[\frac{\sin \frac{(n+1)\pi }{2}}{n+1}+\frac{\sin \frac{(n-1)\pi }{2}}{n-1}\right]\\ & =\frac{E}{\pi }\left[\frac{\cos \frac{n\pi }{2}}{n+1}-\frac{\cos \frac{n\pi }{2}}{n-1}\right]\\ & =\frac{E\cos \frac{n\pi }{2}}{\pi }\cdot \frac{1}{n^2-1}\cdot \left(-2\right)=-\frac{2E\cos \frac{n\pi }{2}}{\pi }\frac{1}{n^2-1}\end{array}$$
展开为：
$$f(t)=\frac{E}{\pi }-\frac{2E}{\pi }\sum _{n=1}^{\infty }\frac{1}{n^2-1}\cos \left(\frac{n\pi }{2}\right)\cos (n{\omega }_{1}t)$$

5. 周期全波余弦信号

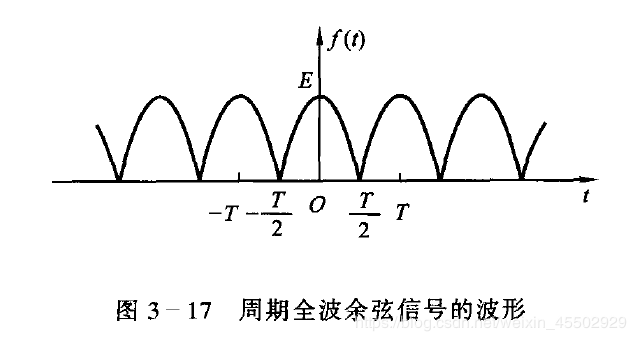
由于这个函数也是偶函数，分析方法与半波余弦信号比较类似，我们尽量利用先前得到的结果。

首先，一个周期内的半个空缺被补上，首项变为原来的两倍，成为半波推导中的$a_0$，即$\frac{2E}{\pi }$。
由于是偶函数，所以我们可以利用偶函数性质，将其系数$A_n$表示成
$$\begin{array}{rl}{A}_n& =\frac{2}{T_1}{\int }_{-\frac{T_1}{4}}^{\frac{T_1}{4}}E\cos ({\omega }_{1}t)\cos (n{\omega }_{1}t)\mathrm{d}t+2\cdot \frac{2}{T_1}{\int }_{\frac{T_1}{4}}^{\frac{T_1}{2}}E(-\cos {\omega }_{1}t)\cos (n{\omega }_{1}t)\mathrm{d}t\\ & =a_n-\frac{4E}{T_1}{\int }_{\frac{T_1}{4}}^{\frac{T_1}{2}}\cos ({\omega }_{1}t)\cos (n{\omega }_{1}t)\mathrm{d}t\end{array}$$
我们计算
$$\begin{array}{rl}{I}_n& =\frac{4E}{T_1}{\int }_{\frac{T_1}{4}}^{\frac{T_1}{2}}\cos ({\omega }_{1}t)\cos (n{\omega }_{1}t)\mathrm{d}t\\ & =\frac{2E}{T_1}{\int }_{\frac{T_1}{4}}^{\frac{T_1}{2}}\cos [(n+1){\omega }_{1}t]+\cos ((n-1){\omega }_{1}t)\mathrm{d}t\\ & =\frac{2E}{{\omega }_1{T}_1}\left(\frac{\sin (n+1)\pi -\sin \frac{n+1}{2}\pi }{n+1}+\frac{\sin (n-1)\pi -\sin \frac{n-1}{2}\pi }{n-1}\right)\mathrm{d}t\\ & =\frac{E}{\pi }\left(\frac{0-\cos \frac{n\pi }{2}}{n+1}+\frac{0+\cos \frac{n\pi }{2}}{n-1}\right)\mathrm{d}t\\ & =\frac{E}{\pi }\cos \frac{n\pi }{2}\left(\frac{1}{n-1}-\frac{1}{n+1}\right)\mathrm{d}t\\ & =\frac{-2E}{\pi }\cos \left(\frac{n\pi }{2}\right)\frac{1}{n^2-1}\end{array}$$

于是我们发现了一个问题：周期全波余弦信号的傅里叶展开是周期半波余弦的直接加倍。

将4.中得到的结果加倍，得到：
$$f(t)=\frac{2E}{\pi }-\frac{4E}{\pi }\sum _{n=1}^{\infty }\frac{1}{n^2-1}\cos \left(\frac{n\pi }{2}\right)\cos (n{\omega }_{1}t)$$
由于$n$为奇数时，系数为0，所以我们取$n=2n$，对系数表达式进行变形：
$$f(t)=\frac{2E}{\pi }+\frac{4E}{\pi }\sum _{n=1}^{\infty }\frac{1}{4n^2-1}(-1{)}^{n+1}\cos (2n{\omega }_{1}t)$$