Python的leastsq()、curve_fit()拟合函数

1、leastsq()与curve_fit()

1.1 leastsq()

  Python中的leastsq()、curve_fit()拟合函数在scipy.optimize模块中，使用时需要导入。
  leastsq()使用最小二乘方法，函数具体形式可以参考官方文档leastsq() 函数，一般我们调用的格式（其余参数默认）：

leastsq(func, x0, args=())
# func:误差函数
# x0: 起始估计的参数值
# arg: 拟合的数据样本

1.2 curve_fit()

  curve_fit()函数具体形式可以参考官方文档curve_fit()函数。一般我们调用格式（其余参数默认）：

curve_fit(func, x, y, p0)
# func：拟合的函数模型，含有待拟合的参数
# x：拟合样本x
# y：拟合样本y
# P0：其实估计的参数值

2、示例

2.1 问题

  利用leastsq()与curve_fit()对高斯分布进行拟合，$x\in [0,10]$，高斯分布函数为$y=a\ast e^{\frac{-(x-b{)}^2}{(2c^2)}}$ , 其中真实值 $a=1,b=5,c=2$,对 y 加入噪 声 之 后 进 行 拟 合 。

2.2 代码

# -*- coding: utf-8 -*-
import numpy as np
from scipy.optimize import leastsq          #导入leastsq模块
from scipy.optimize import curve_fit        #导入leastsq模块
import matplotlib.pyplot as plt             #导入pyplot模块
#####  引用以下3句 在绘图显示中文时不会出现乱码  ####
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False

def func(x, p):
    ## 定义拟合函数 y=a*np.exp(-(x-b)**2/(2*c**2))
    a, b, c = p
    return a*np.exp(-(x-b)**2/(2*c**2))
def residuals(p, y, x):
    #实验数据x, y和拟合函数之间的差，p为拟合需要找到的系数
    return y - func(x, p)
x = np.linspace(0, 10, 100)
a, b, c = 1, 5, 2                           # 真实数据的函数参数
y0 = func(x, [a, b, c])                     # 真实数据
np.random.seed(0)                           # 随机噪声种子
y1 = y0 + 0.02 * np.random.randn(len(x))    # 加入噪声之后的实验数据
P0 = [2, 0.40, 0.2]                         # 第一次猜测的函数拟合参数
result_fit1 = leastsq(residuals,P0,args=(y1,x))#拟合函数
print ("真实参数:", a, b, c)
print ("leastsq方法拟合参数", result_fit1[0]) # leastsq方法拟合参数拟合后的参数
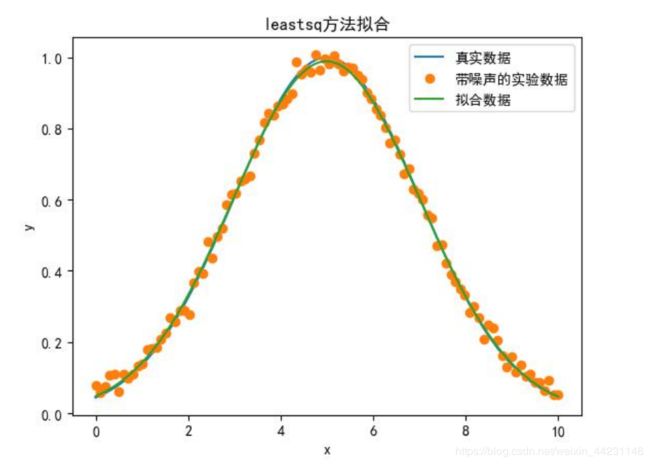
plt.plot(x, y0, label="真实数据")            #绘制真实数据
plt.plot(x, y1,"o", label="带噪声的实验数据") #绘制带有噪声数据
plt.plot(x, func(x, result_fit1[0]), label="拟合数据") #绘制拟合结果
plt.title('leastsq方法拟合')                 #添加标题
plt.xlabel('x')                             #x轴名称
plt.ylabel('y')                             #y轴名称
plt.legend()                                #添加图例
plt.show()                                  #显示图像

def func2(x, a, b, c):                      #定义需要拟合的函数
    return a*np.exp(-(x-b)**2/(2*c**2))
popt, _ = curve_fit(func2, x, y1, p0=P0)    #拟合函数
print ("curve_fit方法拟合参数",popt) # curve_fit方法拟合参数拟合后的参数
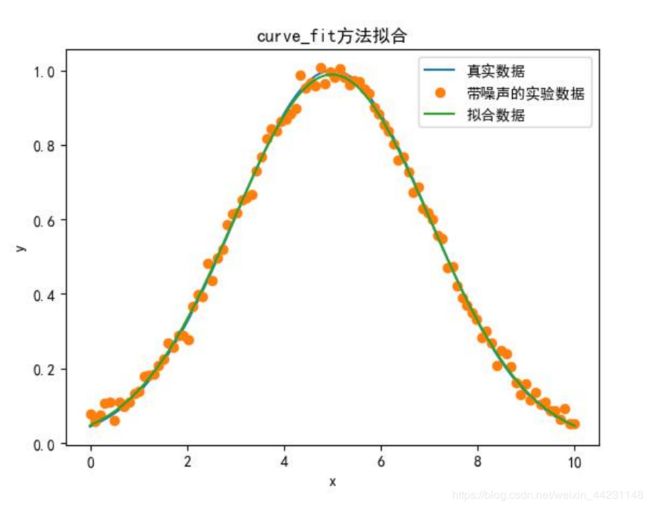
plt.plot(x, y0, label="真实数据")           #绘制真实数据
plt.plot(x, y1,"o", label="带噪声的实验数据") #绘制带有噪声数据
plt.plot(x, func2(x, popt[0],popt[1],popt[2]), label="拟合数据") #绘制拟合结果
plt.title('curve_fit方法拟合')               #添加标题
plt.xlabel('x')                             #x轴名称
plt.ylabel('y')                             #y轴名称
plt.legend()                                #添加图例
plt.show()                                  #显示图像

2.3 结果

真实参数: 1 5 2
leastsq方法拟合参数 [0.98878408 4.99079501 2.02431117]

curve_fit方法拟合参数 [0.98878408 4.99079501 2.02431117]

The End!

！！！请勿抄袭！！！