c/c++实现计算器功能(输入多项表达式 + - x / ,等号输出结果,全清除) 退格操作
c/c++实现计算器功能(输入多项表达式 + - x / ,等号输出结果。)
添加了退格操作,给补上了,在文章最后(附源码)
课程设计实现计算器功能 加减乘除
先讲大概思路,模拟计算器,大家用的计算器都是输入一个表达式然后等号 计算器就会输出结果;
基本的加减乘除 和 数字的混合表达式
首先就要想到表达式的加减乘除符号的判断及其优先级还有小括号。
接下来话不多说 上代码:
#include <iostream>
#include<stdlib.h>
#include<conio.h>
#include<windows.h>
#include<cstring>
using namespace std;
#define MAX 100
char postexp[MAX];//定义的存放操作数的字符数组(就是加减乘除的符号)
用到的头文件
class calculator //计算器类
{
private:
typedef struct //存储数字
{
char n[MAX];
int top;
}SqStack;
typedef struct //存储运算符
{
double n[MAX];
int top;
}SqStack1;
public:
calculator(){}; //空的构造函数
void trans(char *exp,char postexp[]); //算数表达式转换后缀表达式算法
double compvalue(char * postexp); //计算后缀表达式的值
void InitStack(SqStack *&s); //栈初始化
void DestroyStack(SqStack *&s); //销毁栈
bool StackEmpty(SqStack *s); //判断栈空
bool Push(SqStack *&s,char e); //进栈
bool Pop(SqStack *&s,char &e); //出栈
bool GetTop(SqStack *s,char &e); //取栈顶元素
//以下成员函数同上,区别为:参数类型与函数名不同
void InitStack1(SqStack1 *&s);
void DestroyStack1(SqStack1 *&s);
bool StackEmpty1(SqStack1 *s);
bool Push1(SqStack1 *&s,double e);
bool Pop1(SqStack1 *&s,double &e);
bool GetTop1(SqStack1 *s,double &e);
void menu(); //菜单 选择 容错
void Dealy(); //延时函数
};
定义计算器类,然后用到结构体 一个定义给数字,一个定义给运算符。下面是所有成员函数的声明,这里有两部分栈的操作函数(其实内容都一样),分别要用给数字和运算符两个栈,所以要区别名称以调用,(定义两个栈的结构体和两部分栈的操作函数要对应)
void calculator::InitStack(SqStack *&s) //栈初始化
{
s = (SqStack *)malloc(sizeof(SqStack));//分配一个顺序栈空间,首地址存放在S中
s->top = -1;//栈顶指针置为1
}
void calculator::DestroyStack(SqStack *&s)//销毁栈
{
free(s);//释放S的对象
}
bool calculator::StackEmpty(SqStack *s) //判断栈空
{
return(s->top == -1);//判断条件
}
bool calculator::Push(SqStack *&s, char e) //进栈
{
if (s->top == MAX - 1)//栈上溢出
return false;
s->top++;//栈顶指针增1
s->n[s->top] = e;//元素e放栈顶
return true;
}
bool calculator::Pop(SqStack *&s, char &e)//出栈
{
if (s->top == -1)//栈下溢出
return false;
e = s->n[s->top];//取栈顶元素
s->top--;//栈顶指针减1
return true;
}
bool calculator::GetTop(SqStack *s, char &e) //取栈顶元素
{
if (s->top == -1)//栈下溢出
return false;
e = s->n[s->top];//取栈顶元素
return true;
}
void calculator::InitStack1(SqStack1 *&s)
{
s = (SqStack1 *)malloc(sizeof(SqStack1));
s->top = -1;
}
void calculator::DestroyStack1(SqStack1 *&s)
{
free(s);
}
bool calculator::StackEmpty1(SqStack1 *s)
{
return(s->top == -1);
}
bool calculator::Push1(SqStack1 *&s, double e)
{
if (s->top == MAX - 1)
return false;
s->top++;
s->n[s->top] = e;
return true;
}
bool calculator::Pop1(SqStack1 *&s, double &e)
{
if (s->top == -1)
return false;
e = s->n[s->top];
s->top--;
return true;
}
bool calculator::GetTop1(SqStack1 *s, double &e)
{
if (s->top == -1)
return false;
e = s->n[s->top];
return true;
}
这个没什么说的,就是 栈操作的函数(注意函数名称及其所用的栈定义名称要对应)
void calculator::trans(char *exp,char postexp[])
{
char e;
SqStack * Optr;
InitStack(Optr);
int i=0;
while(* exp!='=')
{
switch(* exp)
{
case'(':
Push(Optr,'(');
exp++;
break;
case')':
Pop(Optr,e);
while(e!='(')
{
postexp[i++]=e;
Pop(Optr,e);
}
exp++;
break;
case'+':
case'-':
while(!StackEmpty(Optr))
{
GetTop(Optr,e);
if(e!='(')
{
postexp[i++]=e;
Pop(Optr,e);
}
else
break;
}
Push(Optr,* exp);
exp++;
break;
case'*':
case'/':
while(!StackEmpty(Optr))
{
GetTop(Optr,e);
if(e=='*'||e=='/')
{
postexp[i++]=e;
Pop(Optr,e);
}
else
break;
}
Push(Optr,*exp);
exp++;
break;
default:
while(* exp>='0' && * exp<='9')
{
postexp[i++]=* exp;
exp++;
}
postexp[i++]='#';
}
}
while(!StackEmpty(Optr))
{
Pop(Optr,e);
postexp[i++]=e;
}
postexp[i]='\0';
DestroyStack(Optr);
}
划重点:这个函数和下一个函数是这个程序的关键, 这个是数据结构中的后缀表达式转换 !!!
就是 将输入的算术表达式转换成后缀表达式的算法,这个当时在看数据结构时看的有点绕,不过还是理解了,打大家可以参考《数据结构教程 第五版 李春葆》
double calculator::compvalue(char * postexp)//计算后缀表达式的值
{
double d,a,b,c,e;
SqStack1 * Opnd;//定义操作数栈
InitStack1(Opnd);//初始化操作数栈
while(* postexp!='\0')//postexp字符串未扫描完时循环
{
switch(* postexp)
{
case'+': //判定为‘+’号
Pop1(Opnd,a); //出栈元素a
Pop1(Opnd,b); //出栈元素b
c=b+a; //计算c
Push1(Opnd,c); //将计算结果c进栈
break;
case'-': //判定为‘-’号
Pop1(Opnd,a); //出栈元素a
Pop1(Opnd,b); //出栈元素b
c=b-a; //计算c
Push1(Opnd,c); //将计算结果c进栈
break;
case'*': //判定为‘*’号
Pop1(Opnd,a); //出栈元素a
Pop1(Opnd,b); //出栈元素b
c=b*a; //计算c
Push1(Opnd,c); //将计算结果c进栈
break;
case'/': //判定为‘/’号
Pop1(Opnd,a); //出栈元素a
Pop1(Opnd,b); //出栈元素b
if(a!=0) //分母不为零时,计算
{
c=b/a; //计算c
Push1(Opnd,c); //将计算结果c进栈
break;
}
else
{
printf("\n\t除零错误!\n");
exit(0); //异常退出
}
break;
default: //处理数字字符
d=0; //将连续的数字字符转换成对应的数值存放到d中
while(* postexp>='0' && * postexp<='9') //判定为数字字符
{
d=10*d+*postexp-'0';
postexp++;
}
Push1(Opnd,d); //将数值d进栈
break;
}
postexp++; //继续处理其他字符
}
GetTop1(Opnd,e); //取栈顶元素e
DestroyStack1(Opnd); //销毁栈
return e; //返回e
}
重点!
这个是将转换成的后缀表达式计算出来的算法 即我们最重要得出的计算结果
后缀表达式作为参数传进去
《数据结构教程 第五版 李春葆》
void calculator:: menu() //定义一个calculator类的函数
{ calculator m;
char exp[MAX];
char choice;
int flag=0; //使初始值=0
//操作界面
cout<<" -------------------------------------------"<<"\t\n";
cout<<" - -"<<"\t\n";
cout<<" -------------------------------------------"<<"\t\n";
cout<<" - Welcome TO Use -"<<"\t\n";
cout<<" -------------------------------------------"<<"\t\n";
cout<<" - -"<<"\t\n";
cout<<" - -"<<"\t\n";
cout<<" -------------------------------------------"<<"\t\n";
cout<<" - Calculator -"<<"\t\n";
cout<<" -------------------------------------------"<<"\t\n";
cout<<" - -"<<"\t\n";
cout<<" -------------------------------------------"<<"\t\n";
cout<<"Please enter expression\n";
cout<<"\n --And add the '=' end of the expression:";
//算数表达式 容错机制
int f1=0,i;
while(f1==1 || scanf("%s%*c",&exp))// %*c 为吸收回车字符
{
int l=strlen(exp);//检测输入字符串的长度赋值给l
if(f1==0)
{
i=0;
f1=1;
}
if((exp[i]=='+'||exp[i]=='-'||exp[i]=='*'||exp[i]=='/')&&(exp[i+1]=='+'||exp[i+1]=='-'||exp[i+1]=='*'||exp[i+1]=='/') || (exp[i]>='A' && exp[i]<='Z') || (exp[i]>='a' && exp[i]<='z')||exp[l-1]!='='/*||exp[i]==' '*/)
{
m.Dealy();//调用 报错并延迟画面函数
system("cls");m.menu();//清屏;调用函数本身
}
else if(i==l)
{
break;
}
i++;
}
m.trans(exp,postexp); //进行表达式转换
//cout<
cout<<"\nValue:"<<m.compvalue(postexp)<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl; //计算表达式结果
cout<<"A:全清"<<endl;
cout<<"0:退出"<<endl;
cout<<"Please Choose:";
//选择操作 容错机制
do
{
if(!(cin>>choice)) // 判断是否输入
{
flag=0;
}
else if(!(choice=='A'||choice=='0'))
{
flag=0;
}
else
{
flag=1;break;
}
cout<<"Error Please re-enter:";//错误提示
fflush(stdin);//清楚缓冲区
}while(flag==0);
switch(choice)
{
case 'A':system("cls");m.menu();//清屏函数;返回菜单
case '0' :exit(1);break; //退出程序
default:break;
}
}
界面,然后就是判断用户输入,不能是字母,不能是两个运算符连续输入,然后输入完表达式必须要在输入等号才能回车运行,再者就是计算完一个表达式后可以选择退出程序 或者全清除 再次运行计算
选择退出程序 或者全清除

fflush(stdin);//清楚缓冲区;
这个东西挺有趣,就是scanf这个东西会有缓冲区,会残留上一次的字符,比如你循环输入或许会陷入死循环,具体大家可以去查一查,
void calculator::Dealy()//画面延迟函数
{
int i = 0,j;
cout<<"\n --Warning ,Error expression, Please Re-enter!\t\t\t";
for (i = 1; i <= 100; ++i)
{
printf("\b\b\b\b%3d%%",i);
for (j = 0; j < 2500000; ++j)
{
i++;
i--;
}
}
}
花里胡哨 其实这个没什么大用,为了流程美观(其实美观不美观我也不知道hhhhhh)

就是错误的输入就提示你错了,请重输,延时这个画面随后又跳回最开始的输入界面重新输入(延时时间可以调整,其实很鸡肋)
int main() //主函数
{
calculator m;
m.menu();
return 0;
}
主函数,直接调用menu就ok了,,,
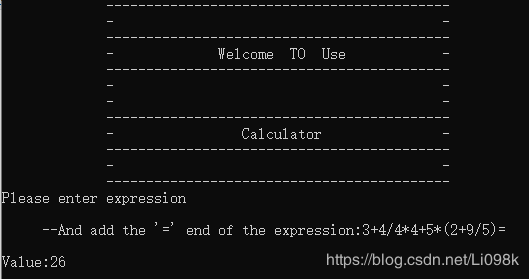
运行一下就是这个效果
遗憾的是不支持小数计算
前些日子有个妹子问之前的c/c++计算器功能中好像没有 退格操作.
所以就改了下之前的代码,算是添加了一段代码进去
退格操作
//清除操作
int j=0; //开始接收表达式,置下标为0
while(1)//对表达式每一个字符输入进行判断
{
char ch;
ch = getch();//接收键入的表达式字符
if( (ch == 'c'||ch == 'C') && j != 0)
//判断键入的字符是否为退格键(c为设置的退格键)
//并且表达式第一个收的字符不能为退格键字符(因为没有格可以退)
{
cout<<"\b \b";
// 如果是退格操作 ,\b 将光标向前移一位,
//(两个\b 退格键字符也要消除,加上被退格的字符,移动两位)
//按下c退格键 造成视觉上当前字符被退格的假象
exp[--j] = ' ';
//因为是视觉上的退格假象,其实被退格的当前字符仍然
//存在exp数组中,所以对此字符复制为空
}
else
//如果不是退格键,是正常输入
{
cout<<ch;
//打印该字符
exp[j] = ch;
//并添加到exp数组中保存
j++;
}
if(ch == '=')//循环终止条件
//表达式尾部以 = 号结束表达式输入
{
break;
}
}
添加了以上代码
上述代码中 exp[]为接收的用户输入的表达式;
源码
下面是全部代码
#include
cout<<"\nValue:"<<m.compvalue(postexp)<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl<<endl; //计算表达式结果
cout<<"A:全清"<<endl;
cout<<"0:退出"<<endl;
cout<<"Please Choose:";
//选择操作 容错机制
do
{
cin>>choice;
if(!(choice=='A'||choice=='0'))
{
flag=0;
}
else
{
break;
}
cout<<"Error Please re-enter:";//错误提示
fflush(stdin);//清楚缓冲区
}while(flag==0);
switch(choice)
{
case 'A':system("cls");m.menu();//清屏函数;返回菜单
case '0' :exit(1);break; //退出程序
default:break;
}
}
void calculator::Dealy()//画面延迟函数
{
int i = 0,j;
cout<<"\n --Warning ,Error expression, Please Re-enter!\t\t\t";
for (i = 1; i <= 100; i++)
{
printf("\b\b\b\b%3d%%",i);
for (j = 0; j < 2500000; j++)
{
}
}
}
int main() //主函数
{
calculator m;
m.menu();
return 0;
}
闲来无事,唉~


